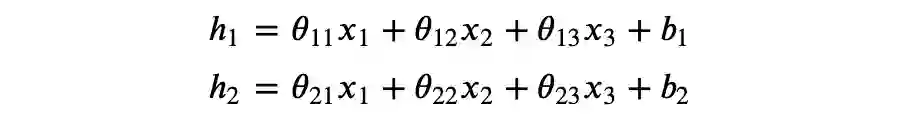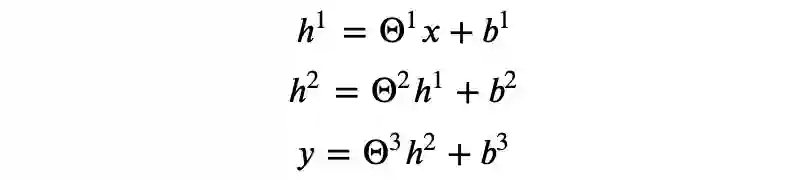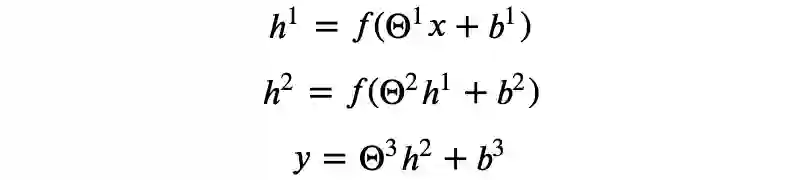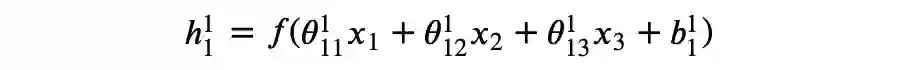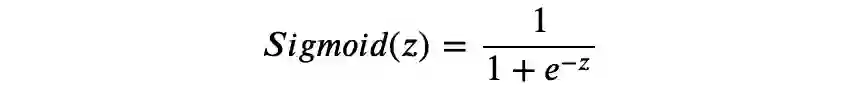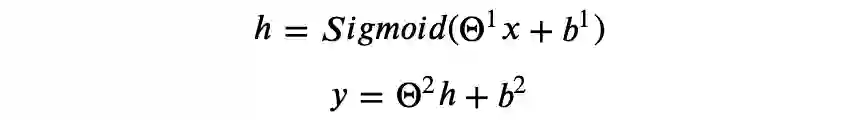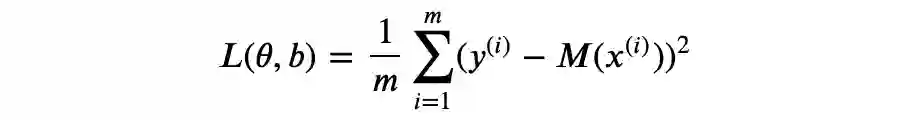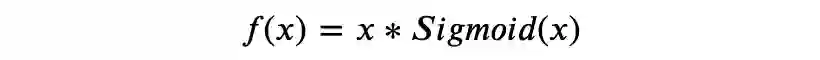一文详解神经网络与激活函数的基本原理
©PaperWeekly 原创 · 作者|王东伟
单位|致趣百川
研究方向|深度学习
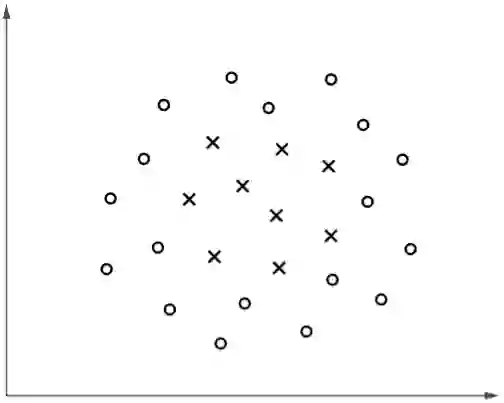
考虑以下分类问题:
▲ 图1
然而,在实际案例中我们通常都无法猜到决策边界的“形状”,一是因为样本的特征数量很大导致无法可视化,二是其可能的特征组合很多。
对于上述非线性模型拟合的问题,我们之前介绍了采用核函数的 SVM,本文将介绍更通用的方法——神经网络。
考虑以下矩阵运算:
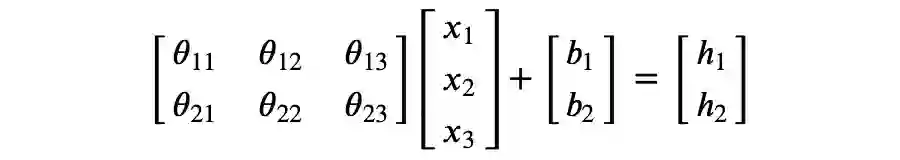
▲ 图2
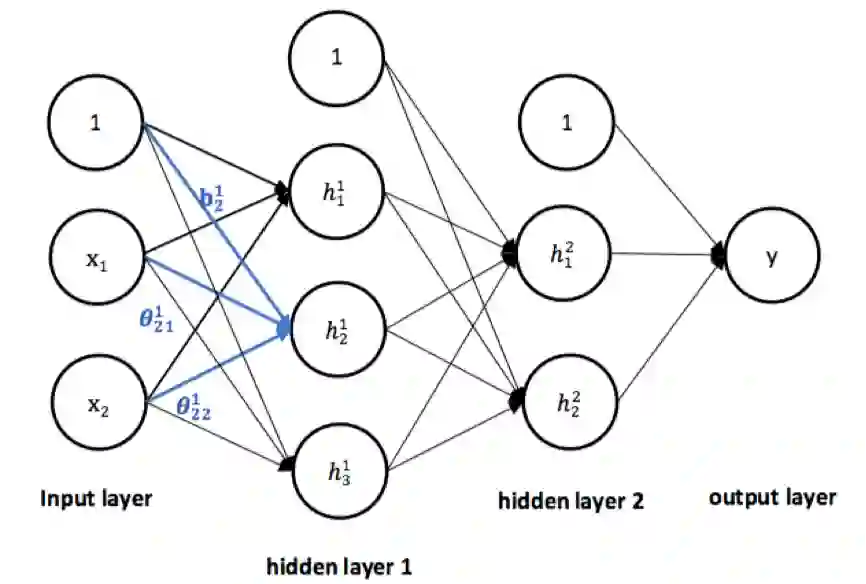
关于神经网络的同义名词。由于部分人不喜欢神经网络与人脑机制的类比,所以他们更倾向于将神经元称为单元,此外,神经网络也被称为多层感知机(multilayer perceptron)。说实话我也不喜欢,但是为了尽可能减少信息差,本文将采用使用率更高的名词。
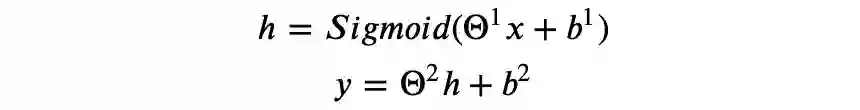
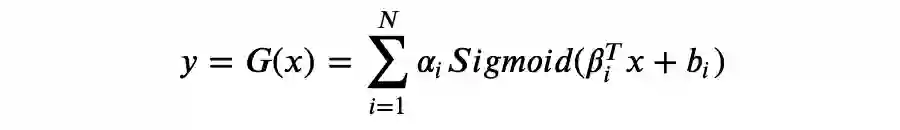
某种意义上,可以认为神经网络自动进行了特征组合,我们需要做的是找到合适的模型架构,并且通过优化算法得到拟合数据样本的模型参数。
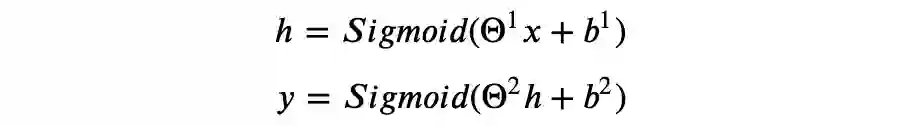
其中:
你可以检验上述运算是否符合矩阵乘法规则。
对于非线性的回归问题,我们模型可以是:
激活函数
▲ 图3.1 Sigmoid
▲ 图3.2 Tanh
Tanh 函数。Tanh 与 Sigmoid 有类似的特征,可以由 Sigmoid 缩放平移得到,即
𝑇𝑎𝑛ℎ(𝑥)=2∗𝑆𝑖𝑔𝑚𝑜𝑖𝑑(𝑥)–1。它的优点是值域为(-1,1)并且关于零点对称,对于零均值的输入将得到零均值的输出,这将有利于更高效的训练(类似于 batch normalization 的作用)。需要注意的是,Tanh 仍然有梯度消失的问题。
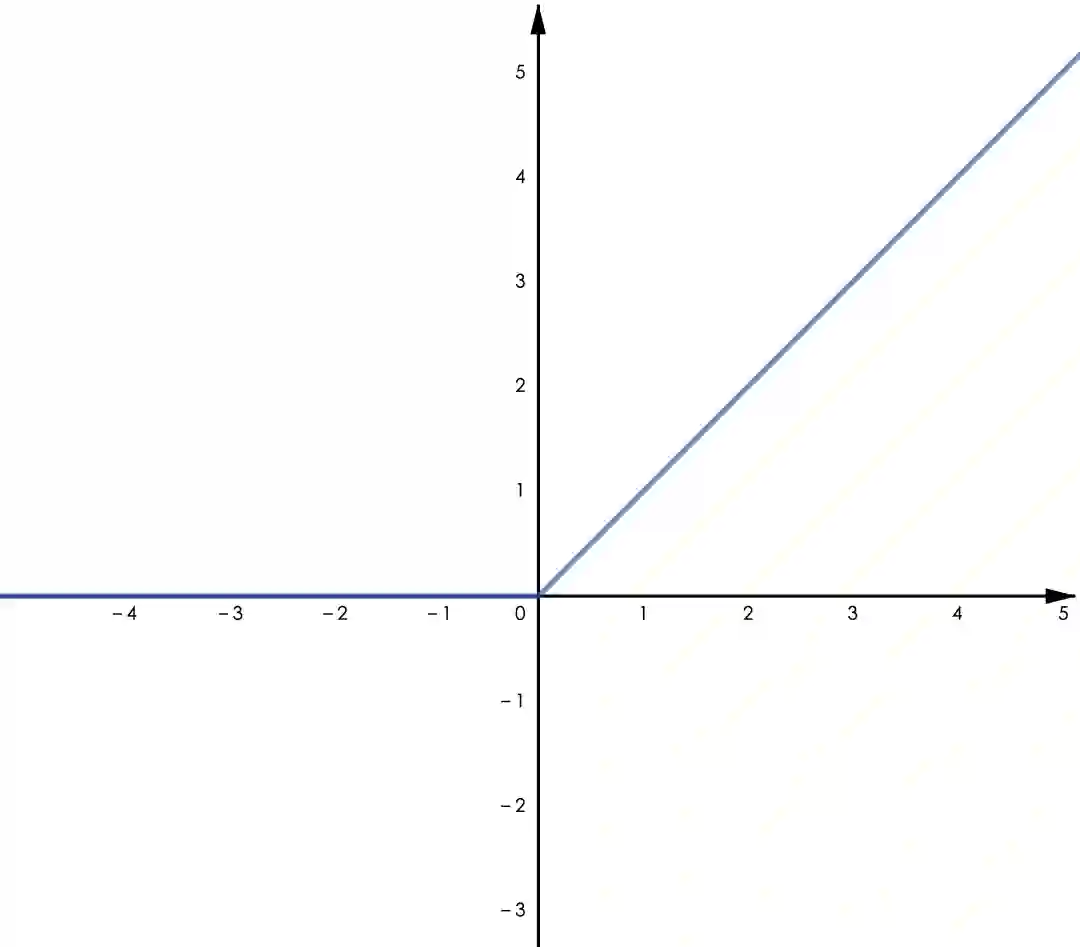
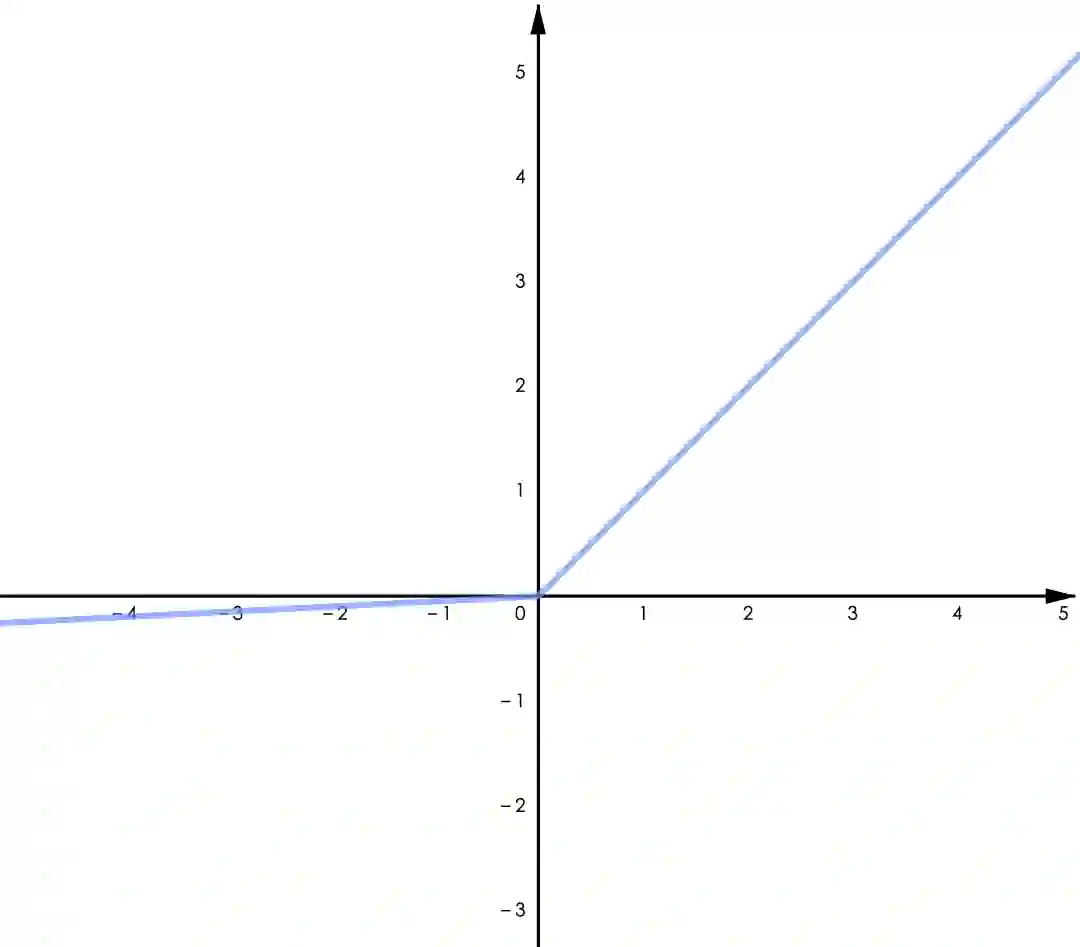
ReLU 函数。表达式为 𝑅𝑒𝐿𝑈(𝑥)=𝑚𝑎𝑥(0,𝑥),一般来说,它相比 Sigmoid 和 Tanh 可以加速收敛,这可能得益于其在正半轴有恒为 1 的梯度,另外由于只需要一次比较运算,ReLU 需要更小的计算量。注意到 ReLU 在负半轴恒为零,这将导致神经元在训练时“永久死亡”(即对于上一层的任何输入,其输出为 0),从而降低模型的拟合能力,事实上,这也是梯度消失的一种表现。
类 ReLU 函数。实践证明 ReLU 在多数任务中具有更优的表现,特别是在深度神经网络中。考虑到 ReLU 本身的缺陷,有许多改进版的 ReLU 被设计出来并得到了不错的效果。主要改进的地方有两点,一是 ReLU 在零点不可导,二是其在负半轴取值为零。其中比较典型的有:
Leaky ReLU:
GELU:
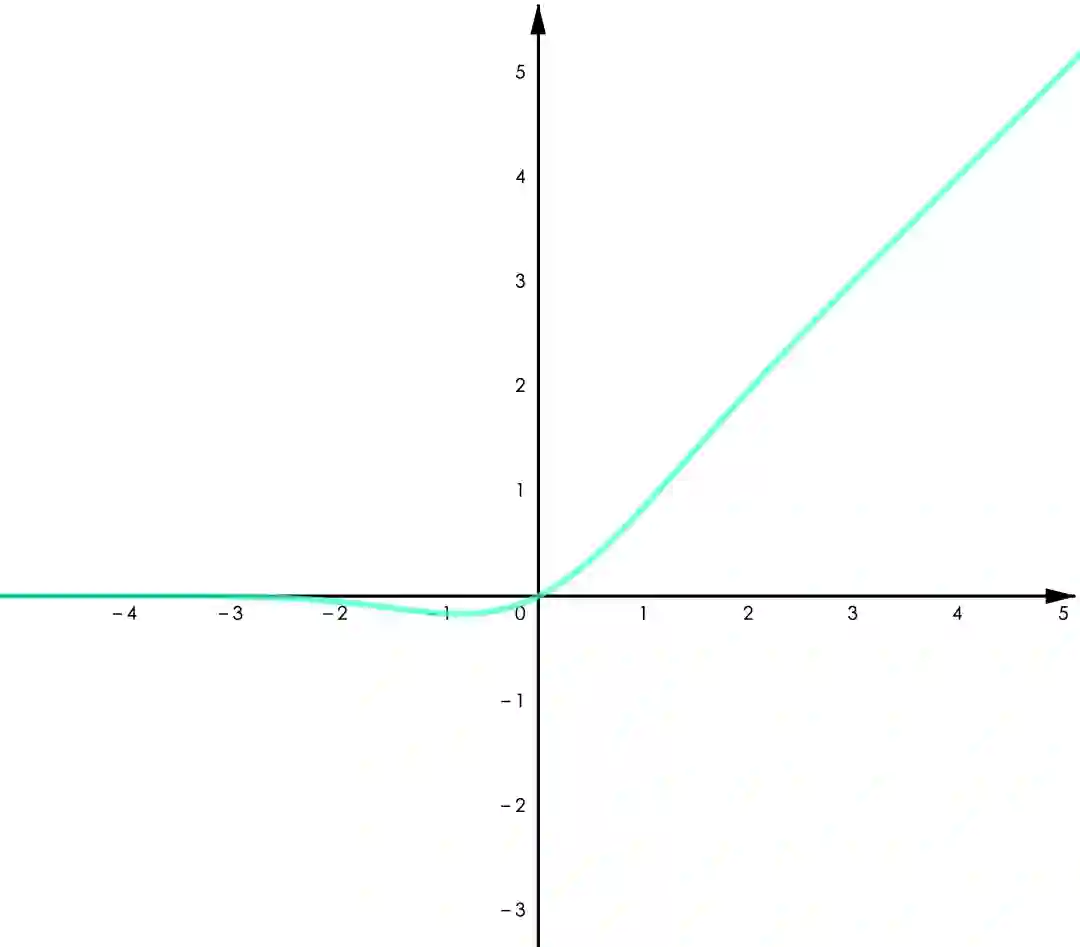
Swish:
▲ 图4.1 ReLU
▲ 图4.2 Leaky ReLU
▲ 图4.3 GELU
▲ 图4.4 Swish
Leaky ReLU 给 ReLU 的负半轴增加了一个微小的梯度,改善了“Dying ReLU”的问题。GELU 用了高斯累计分布来构造 ReLU,著名的 NLP 模型 BERT 用的是 GELU,参考 [1]。Swish 是通过自动化技术搜索得到的激活函数,作者做了大量的对比实验表明 Swish 在不同的任务中均有超出其他类 ReLU 函数的表现(包括 GELU),参考 [2]。
Swish 和 GELU都属于“光滑 ReLU”(smooth ReLU),因为处处连续可导,一篇最近的论文展现了用光滑 ReLU 进行“对抗训练”(adversarial training)的良好表现,参考 [3]。
关于激活函数的选择。没有人任何科学家会 100% 确定地告诉你哪个函数更好用,但是如果按照实验结果,我们可以说类 ReLU 函数目前在多数任务中有更优的表现,就个人的建议,Swish 和 GELU 会是不错的选择,Swish 的论文虽然以实验表明其优于 GELU,但 Google 在 BERT 中使用了 GELU。其他激活函数,可参考 [4]。
上文我们提到了通用近似器的概念,事实上这就是神经网络之所以有效的原因,而其关键的部分则是激活函数。
在“通用近似理论”(universal approximation theorem)领域,可以分为两类近似理论,一类研究任意宽度(arbitrary width)和有界深度(bounded depth)的情况,另一类是任意深度和有界宽度。
比如上文的 G(x) 属于任意宽度和有界深度,即 depth >= 1,width 根据近似的目标函数可以任意调整。在深度学习领域,有很多关于神经网络隐藏层的宽度(width,平均单层神经元数量)和深度(depth,模型层数)如何影响神经网络模型性能的研究,比如,是单层具有 1000 个神经元的隐藏层,还是 10 层具有 100 个神经元的隐藏层表现更好。
值得注意的是,对于某些激活函数,宽度如果小于等于某个数值(对于 ReLU,这个数值是输入特征维数 n),无论其模型深度多大,都存在一些其无法模拟的函数。详情请参考 [5],以及关于深度神经网络的研究 [6]。
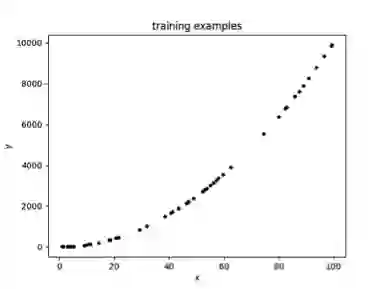
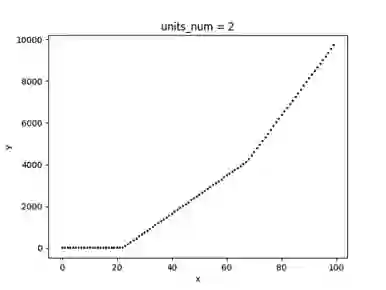
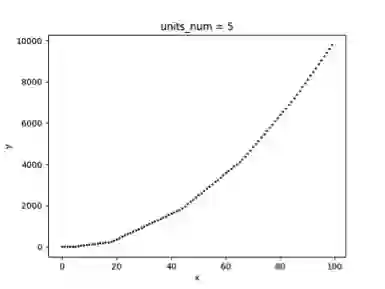
以下一个简单的例子展示了以 ReLU 为激活函数的单隐藏层神经网络模型,其拟合效果与隐藏层单元数量的关系,为了方便可视化,拟合的目标是一元二次函数(x>0)。图 3.1 为随机采样的 50 个样本,图 3.2、3.3、3.4 分别为隐藏层单元数量取 1、2、5 时的拟合曲线。
▲ 图5.1
▲ 图5.2
▲ 图5.3
▲ 图5.4
可以看到随着隐藏层神经元数量的增多,模型的拟合能力逐步增大,如果神经元数量太小,则有可能无法在允许的误差范围内拟合目标函数。
一个有趣的事情是,当我们不用激活函数时,相当于我们用了一个恒等函数 f(x)=x 作为激活函数,这将导致我们的模型只能拟合线性函数。但是,ReLU 仅仅简单地“舍去”负值就取得了通用近似器的效果,有点类似于二极管对交流电的整流作用,这也是 ReLU 名称的由来(Rectified Linear Unit)。
事实上,计算机的运算就是基于开关控制的逻辑电路,所以从这个角度,ReLU 似乎有一种二进制的美感。
参考文献
更多阅读



#投 稿 通 道#
让你的论文被更多人看到
如何才能让更多的优质内容以更短路径到达读者群体,缩短读者寻找优质内容的成本呢?答案就是:你不认识的人。
总有一些你不认识的人,知道你想知道的东西。PaperWeekly 或许可以成为一座桥梁,促使不同背景、不同方向的学者和学术灵感相互碰撞,迸发出更多的可能性。
PaperWeekly 鼓励高校实验室或个人,在我们的平台上分享各类优质内容,可以是最新论文解读,也可以是学习心得或技术干货。我们的目的只有一个,让知识真正流动起来。
📝 来稿标准:
• 稿件确系个人原创作品,来稿需注明作者个人信息(姓名+学校/工作单位+学历/职位+研究方向)
• 如果文章并非首发,请在投稿时提醒并附上所有已发布链接
• PaperWeekly 默认每篇文章都是首发,均会添加“原创”标志
📬 投稿邮箱:
• 投稿邮箱:hr@paperweekly.site
• 所有文章配图,请单独在附件中发送
• 请留下即时联系方式(微信或手机),以便我们在编辑发布时和作者沟通
🔍
现在,在「知乎」也能找到我们了
进入知乎首页搜索「PaperWeekly」
点击「关注」订阅我们的专栏吧
关于PaperWeekly
PaperWeekly 是一个推荐、解读、讨论、报道人工智能前沿论文成果的学术平台。如果你研究或从事 AI 领域,欢迎在公众号后台点击「交流群」,小助手将把你带入 PaperWeekly 的交流群里。