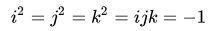透过数学台历看数学(2018.5.4) - 金雀花桥上的灵光一闪

   关注遇见数学, 遇见更精彩的自己

2014 年韩国首尔举行国际数学家大会ICM(http://www.icm2014.org/)中，组委会曾制作了一套数学主题的台历，里面使用数学内容与日历的每一天都相映成趣. [遇见数学] 会按今年日期每天发布这个旧台历上相应的内容。

 — 2018.5.4 —

四元数

四元数

四元数是由哈密顿在1843年爱尔兰发现的。当时他正研究扩展复数到更高的维次（复数可视为平面上的点）。他不能做到三维空间的例子，但四维则造出四元数。根据哈密顿记述，他于10月16日跟他的妻子在都柏林的皇家运河（Royal Canal）上散步时突然想到

的方程解。之后哈密顿立刻将此方程刻在附近布鲁穆桥（Brougham Bridge，现称为金雀花桥 Broom Bridge）。这条方程放弃了交换律，是当时一个极端的想法（那时还未发展出矢量和矩阵）。

金雀花桥上的纪念石刻 | wiki

不只如此，哈密顿还创造了矢量的内外积。他亦把四元数描绘成一个有序的四重实数：一个标量（a）和矢量（bi + cj + dk）的组合。若两个标量部为零的四元数相乘，所得的标量部便是原来的两个矢量部的标量积的负值，而矢量部则为矢量积的值，但它们的重要性仍有待发掘。

哈密顿之后继续推广四元数，并出了几本书。最后一本《四元数的原理》（Elements of Quaternions）于他死后不久出版，长达八百多页。

参考: 维基百科