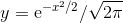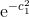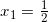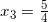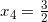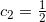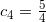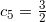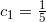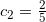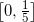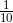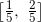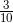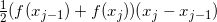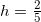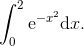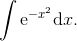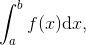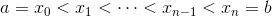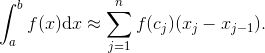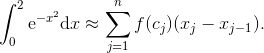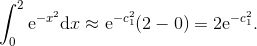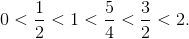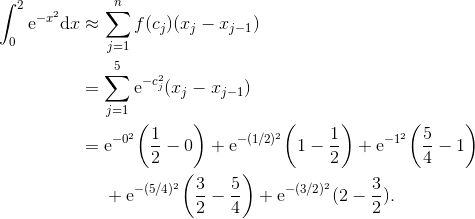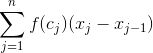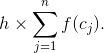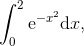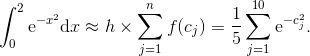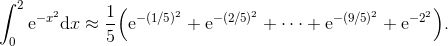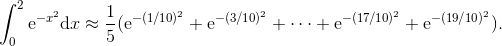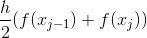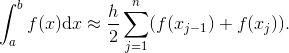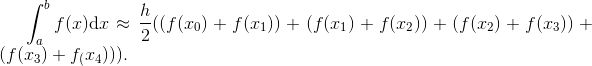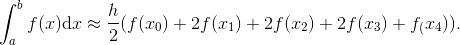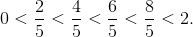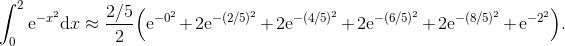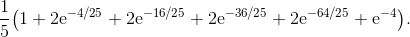使用条纹、梯形法估算积分 - 《普林斯顿微积分读本》

2018 年 10 月 16 日 遇见数学

下文节选自《普林斯顿微积分读本》, 已获出版社授权许可, [遇见数学] 特此表示感谢!

看到定积分时, 我们习惯于通过反导数以及微积分第二基本定理来给出一个确切的答案. 可实际上, 求解一个有用的反导数可能会很困难或者根本不可能. 有时候, 最好的选择是求出一个积分值的近似. 因此, 我们将讨论估算定积分的三种技巧, 以下就是最后这个附录的内容：

使用条纹、梯形法则及辛普森法则估算定积分;
估算上述近似中的误差.

B.1　使用条纹估算积分

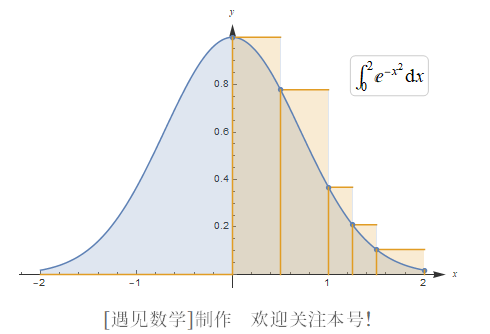
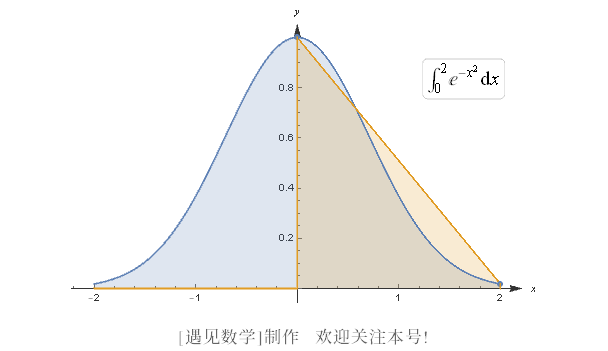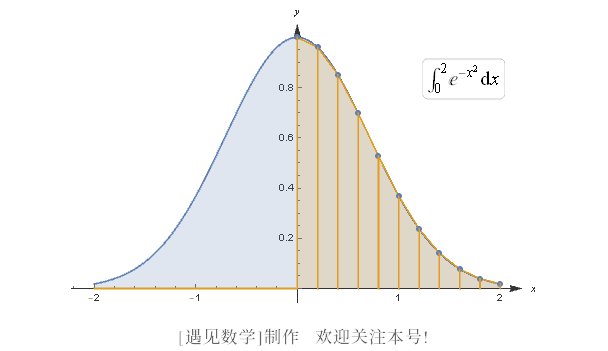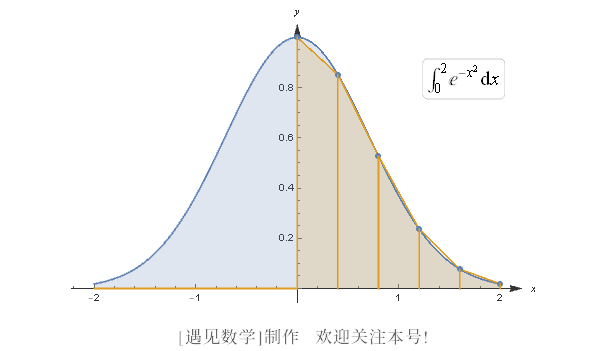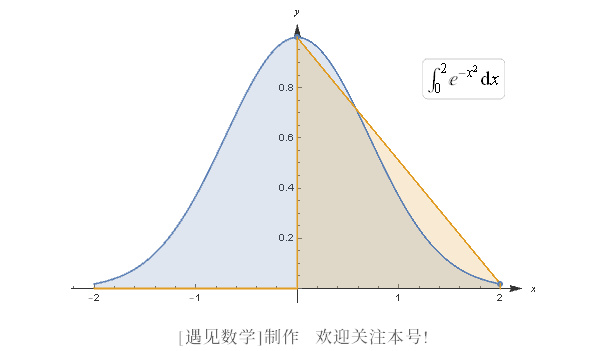
以下是一个完全合理的定积分：

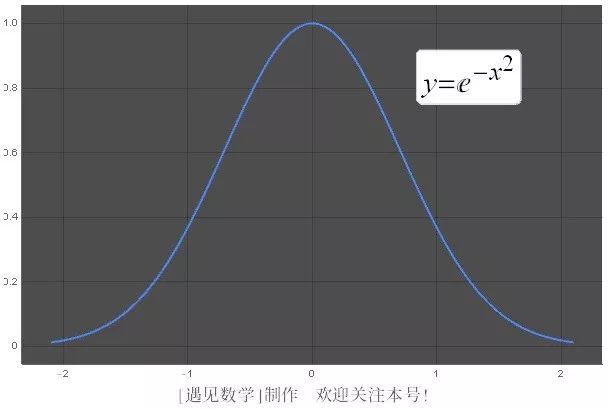
它相当于由 x 轴、曲线 y = e^(-x²) 以及直线 x = 0 与 x = 2 所围成区域的面积, 如图 B-1 所示.

图　B-1

求这样的区域面积或许看起来偏于技术性, 但它有非常大的实际意义. 上述曲线通常被认为是钟形曲线,1 而且它是概率论学习的基础. 因此, 特别烦扰的是, 没有简单的好方法来写出反导数

1技术上说, 钟形曲线 (或正态分布) 实际上是由方程给出的.

实际上, 你可以使用麦克劳林级数把这个积分写成一个无穷级数, 但这也不是简单的好方法. 当前的严峻现实是, 无法将本节最开始的那个定积分的确切值以简洁的方式写出来. (在 16.5.1 节中, 我们已经讨论了这一点. )

另一方面, 我们可以使用黎曼积分的定义求出这个积分的近似值, 即一个估算. 实际上, 在 16.2 节, 我们讨论了划分、区间以及黎曼和. 由于积分是黎曼和的极限, 不取极限, 我们就可以得到一个近似. 因此, 为了估算积分

可以将区间 [a, b] 做一个形如

的划分, 然后在 [x0, x1] 中选取一点 c1, 在 [x1, x2] 中选取一点 c2, 以此类推直到在 [xn-1, xn] 中选取一点 cn. 那时, 就可以写出

这就是说, 积分近似等于它的一个黎曼和.

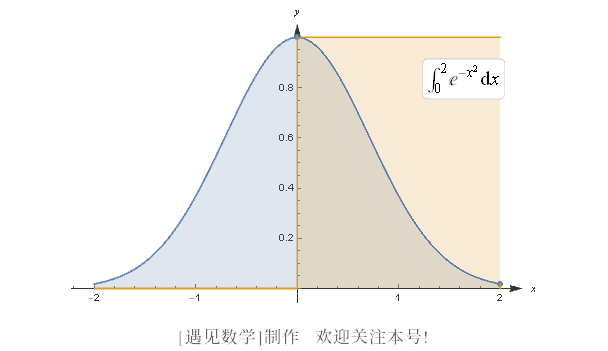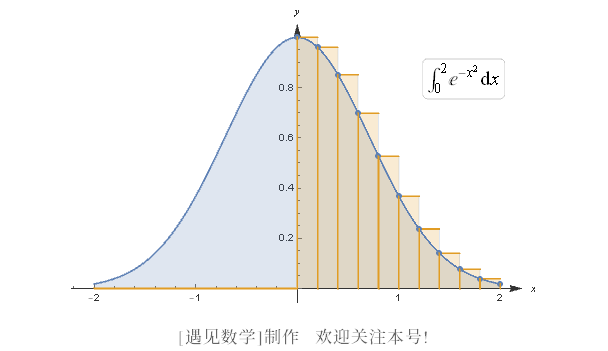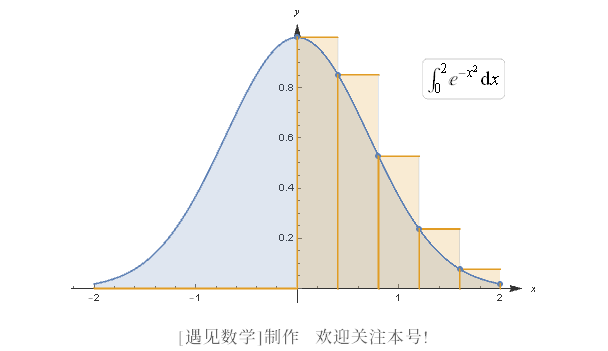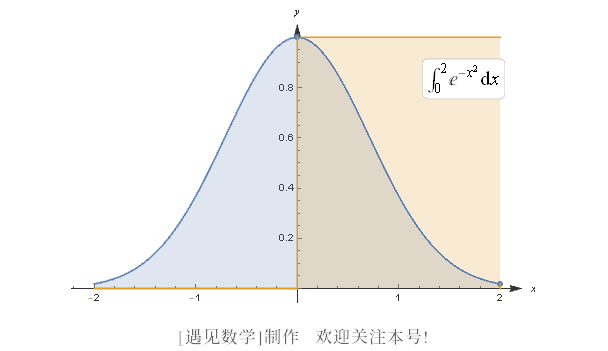
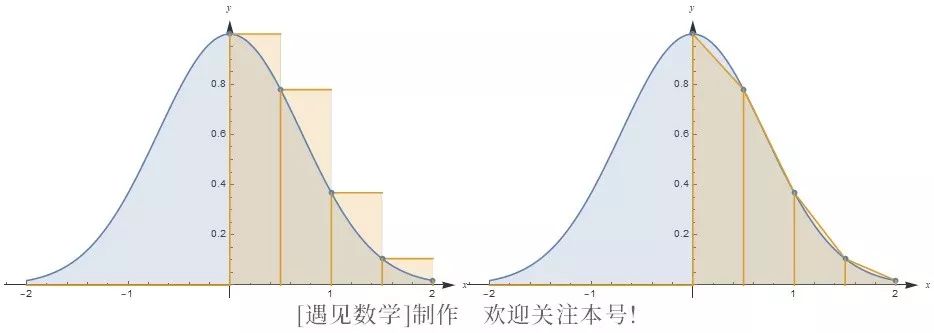
　所有这一切看起来都很抽象. 我们来看看它在上例中是如何起作用的吧. 我们要从 0 到 2 积分, 因此需要区间 [0, 2] 上的一个划分. 该区间上最简单的划分就是这个区间 [0, 2], 这相当于选择 n = 1、x0 = 0 及 x1 = 2. 我们只需要在 [0, 2] 内选取 c1. 求出的近似很大程度上依赖于这个选取! 例如, 如果选取 c1 = 0、c1 = 1 或 c1 = 2, 那么近似就会分别对应图 B-2 所示区域的面积.

图　B-2

很明显, 第一个估算过高了, 而第三个则估算过低了. 中间的那个不算太糟, 但它仍不完美. 为了计算这三个估算值, 我们使用公式

我们用 1 替换 n, 替换 f (c1), 0 替换 x0, 并用 2 替换 x1, 得到

当 c1 是 0、1 或 2 时, 这些值分别是 2、2/e ≈ 0.736 及 2/e4 ≈ 0.037. 正如你看到的, 这三个估算有很大的差别!

　现在我们来看看, 使用更多的条纹是否可以做得更好. 假设我们取了 [0, 2] 上的一个五条划分

因此, n = 5, x0 = 0, , x2 = 1, , , x5 = 2.

假设我们选取的数 cj 是每一个小区间的左端点, 这就表示 c1 = 0, , c3 = 1, , . 将这些数代入上述近似公式中, 可得

　如果你喜欢, 可以再做一些简化, 或者使用计算器或计算机得出其近似到小数点后四位的结果 1.0865. 现在, 你的任务是, 求使用每一个小区间的右端点而不是左端点时的估算值.

均匀划分

取均匀划分总会是很方便的. 这表示, 每一个小区间都有相同的宽度, 并且要计算出其宽度也不是很难的事情. 如果积分区间是 [a, b], 那么其长度是 b - a 单位, 因此如果将该区间 n 等分, 那么每一个小区间的长度是 (b - a) /n 单位. 我们称这个量为 h, 故 h = (b- a) /n. 此外, 出现在黎曼和定义中的表达式 (xj - xj-1) 正是第 j 个条纹的宽度, 因此它正是 h. 我们的表达式

可以简化为

　你仍然需要选取数 cj , 但这一次就简单多了. 例如, 我们使用 10 个等宽的条纹来估算积分

每一条的宽度是 h = (2 - 0) /10, 即 1/5, 而且 n = 10. 因此, 我们有

这些区间的宽度都是 1/5, 因此从 0 开始, 我们看到了如下的划分：

如果我们令 cj 为每一个小区间的右端点, 那么就有 , , 以此类推直到 c10 = 2. 我们将这些数代入上述公式中, 得到

在这个和中有 10 项. 由于函数 f 在 0 和 2 之间是递减的, 而且我们使用了每一条的右端点, 因而以上就是估算过低的情况. (你知道为什么吗？) 不管怎样, 你可以使用计算器或计算机来求上面的和, 大约是 0.783 670(近似到小数点后六位).

如果使用每一个小区间的中点, 而不是左端点或右端点, 情况又会怎样呢？我们知道, 的中点是 , 的中点是 , 以此类推. 因此, 另一个可能的近似是

这大约是 0.882 202.

向上滑动阅览简介及目录

作者者：阿德里安·班纳
译者者：杨爽 , 赵晓婷 , 高璞
出版社：人邮出版社图灵数学

二维码或点击【阅读原文】
跳转遇见微店购买, 然后可领取50-15非图书类优惠券

本书阐述了求解微积分的技巧，详细讲解了微积分基础、极限、连续、微分、导数的应用、积分、无穷级数、泰勒级数与幂级数等内容，旨在教会读者如何思考问题从而找到解题所需的知识点，着重训练大家自己解答问题的能力。

本书适用于大学低年级学生、高中高年级学生、想学习微积分的数学爱好者以及广大数学教师。本书既可作为教材、习题集，也可作为学习指南，同时还有利于教师备课。

第1章函数、图像和直线
1.1 函数
1.1.1 区间表示法
1.1.2 求定义域
1.1.3 利用图像求值域
1.1.4 垂线检验
1.2 反函数
1.2.1 水平线检验
1.2.2 求反函数
1.2.3 限制定义域
1.2.4 反函数的反函数
1.3 函数的复合
1.4 奇函数和偶函数
1.5 线性函数的图像
1.6 常见函数及其图像
第2 章三角学回顾
2.1 基本知识
2.2 扩展三角函数定义域
2.2.1 ASTC方法
2.2.2 （0，2π）以外的三角函数
2.3 三角函数的图像
2.4 三角恒等式
第3 章极限导论
3.1 极限：基本思想
3.2 左极限与右极限
3.3 何时不存在极限
3.4 在∞和—∞处的极限
3.5 关于渐近线的两个常见误解
3.6 三明治定理
3.7 极限的基本类型小结
第4 章求解多项式的极限问题
4.1 x→a时的有理函数的极限
4.2 x→a时的平方根的极限
4.3 x→∞时的有理函数的极限
4.4 x→∞时的多项式型函数的极限
4.5 x→—∞时的有理函数的极限
4.6 包含绝对值的函数的极限
第5 章连续性和可导性
5.1 连续性
5.1.1 在一点处连续
5.1.2 在一个区间上连续
5.1.3 连续函数的一些例子
5.1.4 介值定理
5.1.5 一个更难的介值定理
例子
5.1.6 连续函数的最大值和
最小值
5.2 可导性
5.2.1 平均速率
5.2.2 位移和速度
5.2.3 瞬时速度
5.2.4 速度的图像阐释
5.2.5 切线
5.2.6 导函数
5.2.7 作为极限比的导数
5.2.8 线性函数的导数
5.2.9 二阶导数和更高阶导数
5.2.10 何时导数不存在
5.2.11 可导性和连续性
第6 章求解微分问题
6.1 使用定义求导
6.2 用更好的办法求导
6.2.1 函数的常数倍
6.2.2 函数和与函数差
6.2.3 通过乘积法则求积函数的导数
6.2.4 通过商法则求商函数的导数
6.2.5 通过链式求导法则求复合函数的导数
6.2.6 那个难以处理的例子
6.2.7 乘积法则和链式求导法则的理由
6.3 求切线方程
6.4 速度和加速度
6.5 导数伪装的极限
6.6 分段函数的导数
6.7 直接画出导函数的图像
第7 章三角函数的极限和导数
7.1 三角函数的极限
7.1.1 小数的情况
7.1.2 问题的求解——小数的情况
7.1.3 大数的情况
7.1.4 其他的"情况
7.1.5 一个重要极限的证明
7.2 三角函数的导数
7.2.1 求三角函数导数的例子
7.2.2 简谐运动
7.2.3 一个有趣的函数
第8 章隐函数求导和相关变化率
8.1 隐函数求导
8.1.1 技巧和例子
8.1.2 隐函数求二阶导
8.2 相关变化率
8.2.1 一个简单的例子
8.2.2 一个稍难的例子
8.2.3 一个更难的例子
8.2.4 一个非常难的例子
第9 章指数函数和对数函数
9.1 基础知识
9.1.1 指数函数的回顾
9.1.2 对数函数的回顾
9.1.3 对数函数、指数函数及反函数
9.1.4 对数法则
9.2 e的定义
9.2.1 一个有关复利的问题
9.2.2 问题的答案
9.2.3 更多关于e和对数函数的内容
9.3 对数函数和指数函数求导
9.4 求解指数函数或对数函数的极限
9.4.1 涉及e的定义的极限
9.4.2 指数函数在0附近的行为
9.4.3 对数函数在1附近的行为
9.4.4 指数函数在∞或—∞附近的行为
9.4.5 对数函数在∞附近的行为
9.4.6 对数函数在0附近的行为
9.5 取对数求导法
9.6 指数增长和指数衰变
9.6.1 指数增长
9.6.2 指数衰变
9.7 双曲函数
第10 章反函数和反三角函数
10.1 导数和反函数
10.1.1 使用导数证明反函数存在
10.1.2 导数和反函数：可能出现的问题
10.1.3 求反函数的导数
10.1.4 一个综合性例子
10.2 反三角函数
10.2.1 反正弦函数
10.2.2 反余弦函数
10.2.3 反正切函数
10.2.4 反正割函数
10.2.5 反余割函数和反余切函数
10.2.6 计算反三角函数
10.3 反双曲函数
第11 章导数和图像
11.1 函数的极值
11.1.1 全局极值和局部极值
11.1.2 极值定理
11.1.3 求全局最大值和最小值
11.2 罗尔定理
11.3 中值定理
11.4 二阶导数和图像
11.5 对导数为零点的分类
11.5.1 使用一次导数
11.5.2 使用二阶导数
第12 章绘制函数图像
12.1 建立符号表格
12.1.1 建立一阶导数的符号表格
12.1.2 建立二阶导数的符号表格
12.2 绘制函数图像的全面方法
12.3 例题
12.3.1 一个不使用导数的例子
12.3.2 完整的方法：例一
12.3.3 完整的方法：例二
12.3.4 完整的方法：例三
12.3.5 完整的方法：例四
第13 章最优化和线性化
13.1 最优化
13.1.1 一个简单的最优化例子
13.1.2 最优化问题：一般方法
13.1.3 一个最优化的例子
13.1.4 另一个最优化的例子
13.1.5 在最优化问题中使用隐函数求导
13.1.6 一个较难的最优化例子
13.2 线性化
13.2.1 线性化问题：一般方法
13.2.2 微分
13.2.3 线性化的总结和例子
13.2.4 近似中的误差
13.3 牛顿法
第14 章洛必达法则及极限问题总结
14.1 洛必达法则
14.1.1 类型A：0／0
14.1.2 类型A：±∞／±∞
14.1.3 类型B1：（∞—∞）
14.1.4 类型B2：（0x±∞）
14.1.5 类型C：1±∞，00或∞0
14.1.6 洛必达法则类型的总结
14.2 关于极限的总结
第15 章积分
15.1 求和符号
15.1.1 一个有用的求和
15.1.2 伸缩求和法
15.2 位移和面积
15.2.1 三个简单的例子
15.2.2 一段更常规的旅行
15.2.3 有向面积
15.2.4 连续的速度
15.2.5 两个特别的估算
第16 章定积分
16.1 基本思想
16.2 定积分的定义
16.3 定积分的性质
16.4 求面积
16.4.1 求通常的面积
16.4.2 求解两条曲线之间的面积
16.4.3 求曲线与y轴所围成的面积
16.5 估算积分
16.6 积分的平均值和中值定理
16.7 不可积的函数
第17 章微积分基本定理
17.1 用其他函数的积分来表示的函数
17.2 微积分的第一基本定理
17.3 微积分的第二基本定理
17.4 不定积分
17.5 怎样解决问题：微积分的第一基本定理
17.5.1 变形1：变量是积分下限
17.5.2 变形2：积分上限是一个函数
17.5.3 变形3：积分上下限都为函数
17.5.4 变形4：极限伪装成导数
17.6 怎样解决问题：微积分的第二基本定理
17.6.1 计算不定积分
17.6.2 计算定积分
17.6.3 面积和绝对值
17.7 技术要点
17.8 微积分第一基本定理的证明
第18 章积分的方法I
18.1 换元法
18.1.1 换元法和定积分
18.1.2 如何换元
18.1.3 换元法的理论解释
18.2 分部积分法
18.3 部分分式
18.3.1 部分分式的代数运算
18.3.2 对每一部分积分
18.3.3 方法和一个完整的例子
第19 章积分的方法II
19.1 应用三角恒等式的积分
19.2 关于三角函数的幂的积分
19.2.1 sin或cos的幂
19.2.2 tan的幂
19.2.3 sec的幂
19.2.4 cot的幂
19.2.5 csc的幂
19.2.6 约化公式
19.3 关于三角换元法的积分
19.3.1 类型1：pa2？x2
19.3.2 类型2：px2+a2
19.3.3 类型3：px2？a2
19.3.4 配方和三角换元法
19.3.5 关于三角换元法的总结
19.3.6 平方根的方法和三角换元法
19.4 积分技巧总结
第20 章反常积分：基本概念
20.1 收敛和发散
20.1.1 反常积分的一些例子
20.1.2 其他破裂点
20.2 关于无穷区间上的积分
20.3 比较判别法（理论）
20.4 极限比较判别法（理论）
20.4.1 函数互为渐近线
20.4.2 关于判别法的陈述
20.5 p判别法（理论）
20.6 绝对收敛判别法
第21 章反常积分：如何解题
21.1 如何开始
21.1.1 拆分积分
21.1.2 如何处理负函数值
21.2 积分判别法总结
21.3 常见函数在∞和—∞附近的表现
21.3.1 多项式和多项式型函数在∞和—∞附近的表现
21.3.2 三角函数在∞和—∞附近的表现
21.3.3 指数在∞和—∞附近的表现
21.3.4 对数在∞附近的表现
21.4 常见函数在0附近的表现
21.4.1 多项式和多项式型函数在0附近的表现
21.4.2 三角函数在0附近的表现
21.4.3 指数函数在0附近的表现
21.4.4 对数函数在0附近的表现
21.4.5 更一般的函数在0附近的表现
21.5 如何应对不在0或1处的瑕点
第22 章数列和级数：基本概念
22.1 数列的收敛和发散
22.1.1 数列和函数的联系
22.1.2 两个重要数列
22.2 级数的收敛与发散
22.3 第n项判别法（理论）
22.4 无穷级数和反常积分的性质
22.4.1 比较判别法（理论）
22.4.2 极限比较判别法（理论）
22.4.3 p判别法（理论）
22.4.4 绝对收敛判别法
22.5 级数的新判别法
22.5.1 比式判别法（理论）
22.5.2 根式判别法（理论）
22.5.3 积分判别法（理论）
22.5.4 交错级数判别法（理论）
第23 章求解级数问题
23.1 求几何级数的值
23.2 应用第n项判别法
23.3 应用比式判别法
23.4 应用根式判别法
23.5 应用积分判别法
23.6 应用比较判别法、极限比较判别法和p判别法
23.7 应对含负项的级数
第24 章泰勒多项式、泰勒级数和幂级数导论
24.1 近似值和泰勒多项式
24.1.1 重访线性化
24.1.2 二次近似
24.1.3 高阶近似
24.1.4 泰勒定理
24.2 幂级数和泰勒级数
24.2.1 一般幂级数
24.2.2 泰勒级数和麦克劳林级数
24.2.3 泰勒级数的收敛性
24.3 一个有用的极限
第25 章求解估算问题
25.1 泰勒多项式与泰勒级数总结
25.2 求泰勒多项式与泰勒级数
25.3 用误差项估算问题
25.3.1 第一个例子
25.3.2 第二个例子
25.3.3 第三个例子
25.3.4 第四个例子
25.3.5 第五个例子
25.3.6 误差项估算的一般方法
25.4 误差估算的另一种方法
第26 章泰勒级数和幂级数：如何解题
26.1 幂级数的收敛性
26.1.1 收敛半径
26.1.2 求收敛半径和收敛区域
26.2 合成新的泰勒级数
26.2.1 代换和泰勒级数
26.2.2 泰勒级数求导
26.2.3 泰勒级数求积分
26.2.4 泰勒级数相加和相减
26.2.5 泰勒级数相乘
26.2.6 泰勒级数相除
26.3 利用幂级数和泰勒级数求导
26.4 利用麦克劳林级数求极限
第27 章参数方程和极坐标
27.1 参数方程
27.2 极坐标
27.2.1 极坐标与笛卡儿坐标互换
27.2.2 极坐标系中画曲线
27.2.3 求极坐标曲线的切线
27.2.4 求极坐标曲线围成的面积
第28 章复数
28.1 基础
28.2 复平面
28.3 复数的高次幂
28.4 解zn=w
28.5 解ez=w
28.6 一些三角级数
28.7 欧拉恒等式和幂级数
第29 章体积、弧长和表面积
29.1 旋转体的体积
29.1.1 圆盘法
29.1.2 壳法
29.1.3 总结和变式
29.1.4 变式1：区域在曲线和y轴之间
29.1.5 变式2：两曲线间的区域
29.1.6 变式3：绕平行于坐标轴的轴旋转
29.2 一般立体体积
29.3 弧长
29.4 旋转体的表面积
第30 章微分方程
30.1 微分方程导论
30.2 可分离变量的一阶微分方程
30.3 一阶线性方程
30.4 常系数微分方程
30.4.1 解一阶齐次方程
30.4.2 解二阶齐次方程
30.4.3 为什么特征二次方程适用
30.4.4 非齐次方程和特解
30.4.5 求特解
30.4.6 求特解的例子
30.4.7 解决yP和yH间的冲突
30.4.8 IVP
30.5 微分方程建模
附录A 极限及其证明
A.1 极限的正式定义
A.2 由原极限产生新极限
A.3 极限的其他情形
A.4 连续与极限
A.5 再谈指数函数和对数函数
A.6 微分与极限
A.7 泰勒近似定理的证明
附录B 估算积分
B.1 使用条纹估算积分
B.2 梯形法则
B.3 辛普森法则
B.4 近似的误差
符号列表
索引

B.2　梯形法则

涉及选取数 cj 的问题是很困难的. 大多数情况下, 人们或者选择左端点或者选择右端点, 中点也是个常见的 (并且合理的) 选择. 这里还有一种估算积分的方法, 它不需要选择 (当然是在你决定使用这种方法的时候!) 但会给出更好的估算. 它被称作梯形法则.

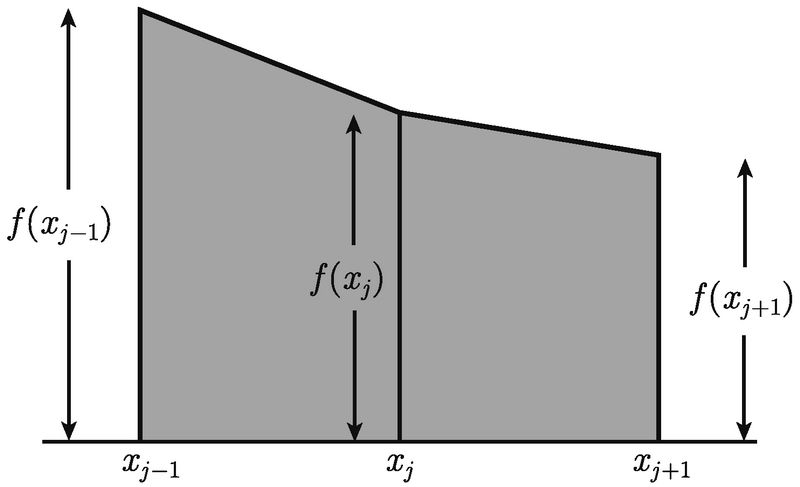
其基本思想非常简单：我们允许条纹的上边不平行于底边. 每一条纹的上边都是连接曲线 y = f (x) 上的两个相应点的线段. 图 B-3 就是说明这两种方法间区别的图像.

图　B-3

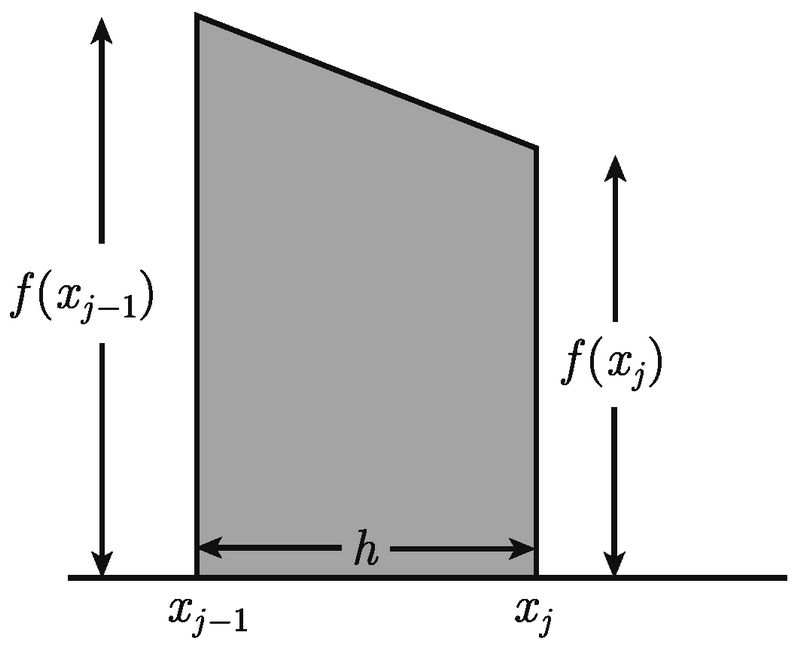
让我们来好好看看其中的一条新条纹, 如图 B-4 所示.

图　B-4

由于有两条边是平行的, 故该条纹是一个梯形. 底边长是 (xj - xj-1) 单位, 而平行的边的高度为 f (xj-1) 单位和 f (xj) 单位. 根据梯形面积公式, 这个梯形条纹的面积是平方单位. 如果我们确保划分都是均匀的, 那么如同上一节, 可知 xj - xj-1 就是 (b - a) /n. 这恰好就是条纹的宽度 (单位), 我们称之为 h, 因此, 一个条纹的面积变为