FaSTrack：安全实时的导航系统

选文| 周艺   翻译| 叶培楚 徐礼达 张晨 胡琪  

校对| 周艺   编辑| 周艺

素材来源：Bair Blog
泡泡机器人推广内容组编译作品

问题：快速安全的运动规划

实时自主运动规划和导航很困难，特别是在安全性方面。当系统具有复杂的动力学、外部扰动（如风）和先验未知环境时，这就变得更加困难了。我们在这项工作的目标是为现有的实时运动规划增加鲁棒性，从而保证导航的安全性。

 

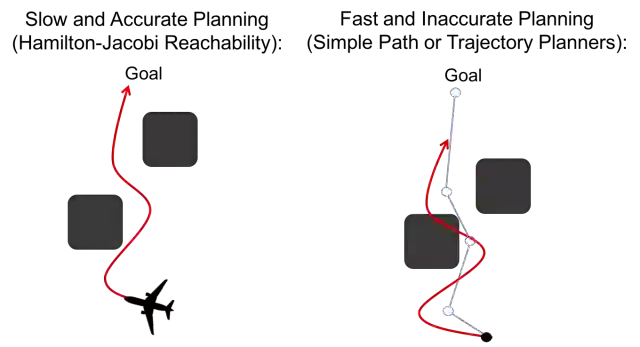
在控制理论中，像Hamilton-Jacobi可达性分析这样的技术提供了严格的系统行为安全保证，同时还有一个最优控制器来达到一个给定的目标（见图1）。 然而，一般来说，由于“维度的诅咒”，HJ可达性分析中使用的计算方法仅适用于可分解和/或低维系统。这意味着对于实时规划，我们无法处理二维以上系统的安全轨迹。 由于汽车，飞机和四旋翼等大多数现实世界的系统模型具有两个以上的维度，这些方法通常是难以实时运行的。

 

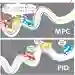
另一方面，像快速探索随机树（RRT）和模型预测控制（MPC）等几何运动规划器可以通过使用简化的系统动力学模型在较短的预测时间域内进行实时规划。虽然这使得我们可以执行实时的运动规划，但是由此产生的轨迹可能过于简化，导致不可避免的碰撞，甚至可能是不可行的（见图1）。 例如，想象一下骑自行车，跟随行人追踪的路径。 这条路通向一棵树，然后在最后一秒转90度。你不能让你的自行车如此急转弯，而是最终撞上树。 通常，机器人专家通过假设障碍比规划中的实际情况略大，从而缓解了这个问题。 这大大提高了不崩溃的机会，但仍然不提供保证，并可能导致意外的碰撞。

 

那么，如何将快速规划的速度与慢规划的安全保障结合起来呢？

图1：在左边，在左边我们有一个高维的飞机通过一个障碍门到达一个目标。计算最优安全轨迹是一个缓慢的、有时棘手的任务，重新规划几乎是不可能的。在右边，我们简化了车辆的模型(在这个例子中，假设它在目标点之间直线移动)。这让我们可以快速地规划，但是当我们执行规划的轨迹时，我们可能会发现它实际上不能正确地沿着路径走，最后会崩溃。

解决方案：FaSTrack

FaSTrack：快速和安全的追踪，实质上是给快速的运动规划方法，如RRT或MPC，增加鲁棒性，同时保持实时性能。FaSTrack允许用户使用简化的动力学模型进行快速运动规划器，同时以规划界限的形式保持安全。规划的状态与运行时的实际状态之间的最大距离，称之为跟踪误差界限。这个预计算还导致了一个最优控制查找表，它为系统提供最优的误差反馈控制器，实时地执行在线规划。

图2： FaSTrack背后的想法是使用简化模型（蓝色），预先计算跟踪误差界限，以捕捉由于模型不匹配和环境干扰（如风）导致的轨迹的潜在偏差，并误差反馈控制使误差保持在界限内。 我们可以通过增加跟踪误差界限来扩大障碍，这保证了我们的动态系统（红色）保持安全。 扩大障碍物的边界在机器人领域并不是一个新概念，但是通过使用我们的跟踪误差界限，我们可以考虑到系统动力学和其他干扰。

离线预计算

我们通过将问题视为规划和跟踪之间的追逃游戏来预先计算这个跟踪误差。为了实时规划，规划器使用系统的简化模型; 跟踪器使用更准确的系统模型。我们假设追踪器（真正的系统）总是追着规划器。 我们想知道在最坏的情况下（当规划器正在积极地试图逃脱追踪器时）最大相对距离（即最大跟踪误差）是多少。 如果我们有这个界限的上限，那么我们即知道运行时可能出现的最大跟踪误差。

图3.跟踪系统使用复杂的真实系统，规划系统使用非常简单的模型，跟踪系统追着规划系统。

因为我们关心最大跟踪误差，所以我们关心最大相对距离。 因此，为了解决这个追逃游戏，我们必须首先确定两个系统之间的相对动力学：将规划器固定在原点并确定跟踪器相对于规划器的动力学。 然后，我们用一个成本函数衡量到这个原点的距离，即跟踪器到规划器的相对距离，如图4所示。跟踪器将尝试最小化这个成本，规划器将尝试最大化它。随着时间推移演变这些最优轨迹，并捕捉在这段时间内发生的最高成本。如果追踪器总是能成功跟上计划者，那么这个成本总是会收敛到一个固定值。

如图5所示，收敛的价值函数的最小不变水平集（level set）决定了跟踪误差界。此外，收敛的价值函数的梯度可以用来为跟踪器创建最优的误差反馈控制策略来追踪计划器。 我们使用Ian Mitchell的水平集工具箱和可达性分析来解决这个微分博弈问题（differential game）。 关于优化的更全面的解释，请参阅我们在2017 IEEE Conference on Decision and Control上的文章。

图4和图5：在左边，我们展示了价值函数的初始和根据微分博弈演化过程。在右边展示了价值函数的3D和2D切片。 每个切片可以被认为是“候选跟踪误差界”。随着时间的推移，这些界限中的一些将变得不可行。 但收敛的价值函数的最小不变水平集为我们提供了可行的跟踪误差界。

在线实时规划

在线阶段，我们在测量半径内测量障碍物，并把障碍物与追踪的误差界限进行Minkowski求和。根据这些扩大的障碍物，运动计划器来决定下一时刻的状态。基于跟踪器和规划器之间的相对状态，根据预设的查找表来确定跟踪器的最优控制。系统执行最佳控制，并重复该过程直到达到目标。这意味着运动的规划器可以继续快速进行规划，并且只需增加障碍物并使用查找表进行控制，我们就可以确保安全性。

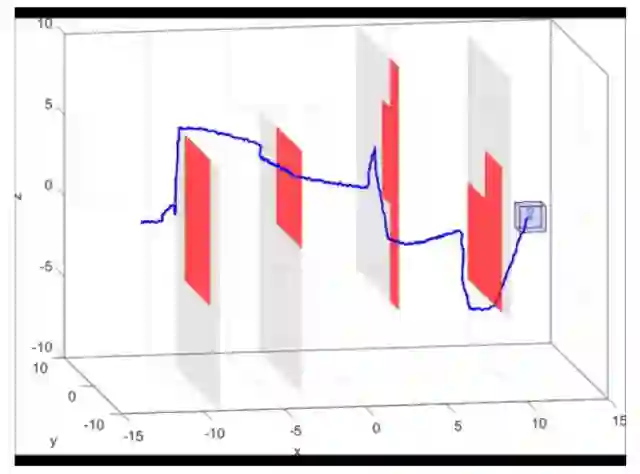
图6. 利用MATLAB仿真了10D接近悬停的四旋翼模型（蓝线） “追”一个使用RRT进行规划的3D规划模型（绿点）。当新的障碍被发现时（变红），RRT计划了一条新的通向目标的道路。根据规划器与系统之间的相对状态，利用查找表得到最优控制。即使RRT规划器要求一个急转弯，我们也能保证跟踪误差不超出误差界（蓝框）。

通过元规划减少保守性

将安全跟踪问题作为规划器和跟踪器之间的追逃博弈的一个后果是，由此产生的安全跟踪界限通常是相当保守的。也就是说，如果策划器总是被允许做最糟糕的行为，跟踪器不能保证它将接近策划器。其中一个解决方案是在计划时间内同时使用多个计划模型，每个规划模型都有自己的跟踪误差界限。由此产生的“元规划”由每个计划器计算出的轨迹段组成，每个轨迹段标有合适的最优控制器来跟踪该规划器生成的轨迹。如图7，其中大的蓝色误差界限对应于被允许非常快速移动的规划器，而小的红色界限对应于移动得更慢的规划器

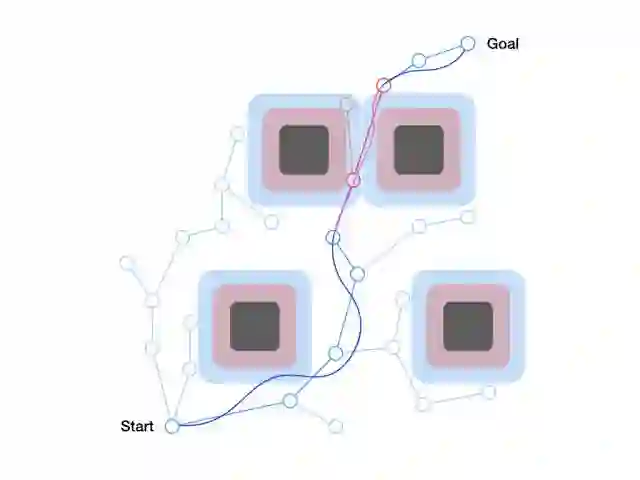
图7.通过考虑两个不同的规划器，每个规划器都有不同的跟踪误差界限。我们的算法能够找到一个保证安全的“元规划”，一般情况下它会选择精确度较低但速度较快的蓝色规划器，但在障碍物附近回到精确更高但较慢红色规划器。这是在保守性和操纵速度之间的最优妥协。

安全转换

实现以上方法的关键在于确保所有规划中的转变都是安全的。这可能有点复杂，但是主要的思路是：如果我们能保证A的不变集包含于B中，则两个规划器A，B之间的转变是安全的。对于许多组规划器来说这是成立的，例如在图7中从蓝色边界转换到红色边界的过程。但也不全是这种情况。通常来说，我们需要解决一个与FaSTrack最初遇到的情况非常相似的动态博弈，我们想找到一个状态集，我们并不会离开这个集，并且从这个集我们可以进入B的不变集。通常得到的安全转换界(SSB)要比A的误差界(TEB)稍微大一些。

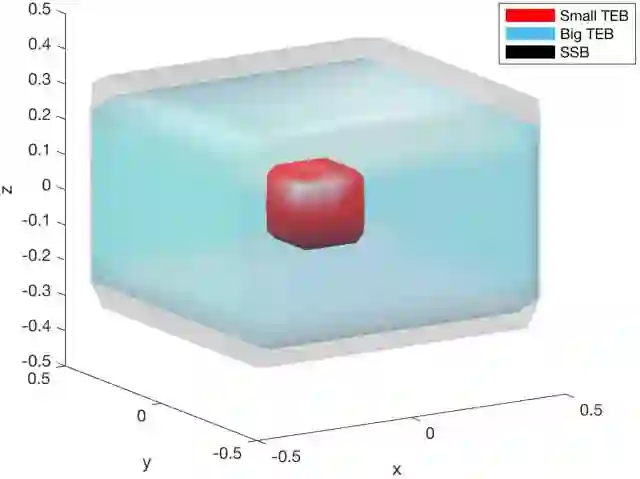
图8大的跟踪误差界的规划器到较小跟踪误差界的安全转换界通常都比那个大的跟踪误差界还要大。

高效的在线元规划

为了实时高效地完成元规划，我们利用一个传统RRT算法的修改版本。通常，RRT通过在状态空间中采样数据点并用线段连接来形成一个以起点为根的树。在我们的方案中，我们利用独立规划器生成的轨迹来替换线段。为了找到目标点最近的路径，我们希望能够移动得更快点，所以优先尝试移动快速的规划器，当且仅当在这类规划失败的情况下才切换到慢的规划器。

但是，我们必须确保能够满足安全转换边界。尤其是当元规划决定转换到更准确但更缓慢的规划时，就像上文提到的那样。在这种情况下，我们实施了一个单步虚拟回溯的算法，利用转换控制器来确保前方轨迹段不会发生碰撞。

实施

我们在C++/ROS运行了FaSTrack和元规划，利用开源运动规划库（OMPL）中的低级运动规划器。仿真结果如下所示，带有优化控制器的在右边，没有优化控制器的在左边。如你们所见，简单地利用线性反馈（LQR）控制器（左边）无法保证规划在跟踪误差界内。

数字9&10.(左边)一个标准LQR控制器不能保持无人机在跟踪误差界内 (右边)最优跟踪控制器保持无人机在跟踪界内，甚至在规划轨迹发生大的变化时仍能保持。

该算法同样能在硬件上工作！我们在开源Crazyflie2.0无人机平台进行了测试。如你们在图12所见，我们控制无人机一直待在跟踪界内，即使规划轨迹发生变化。

数字11&12.（左边）利用一个OptiTrack运动捕捉系统观测Crazyflie2.0四旋翼。（右边）元规划算法在硬件测试时的位置轨迹。如图所示，即使在4.5秒进行规划转换时，跟踪系统也一直保持在跟踪误差界以内。

这篇文章是基于下列文章的工作展开的：

· FaSTrack: a Modular Framework for Fast and Guaranteed Safe Motion Planning
Sylvia Herbert*, Mo Chen*, SooJean Han, Somil Bansal, Jaime F. Fisac, and Claire J. Tomlin
Paper, Website

· Planning, Fast and Slow: A Framework for Adaptive Real-Time Safe Trajectory Planning
David Fridovich-Keil*, Sylvia Herbert*, Jaime F. Fisac*, Sampada Deglurkar, and Claire J. Tomlin

我们非常感谢共同作者；开发FaSTrack是整个团队的努力，我们极其幸运地在这个项目中拥有这群出色的同事。

#泡泡机器人新闻社-往期回顾#

【泡泡机器人新闻社】基于神经网络动力学模型的强化学习

【泡泡机器人新闻社】使用AI和VR技术来教授机器人新技能（内附演示视频和文献）

【泡泡机器人新闻社】ROS的起源：机器人领域的Linux