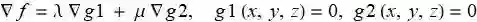【Lagrange 乘子】图解高等数学-下 15

11.8 Lagrange 乘子

如果是求定义域内约束在某个区域内函数的极值, 可以用本次讲述的 Lagrange乘子法.

约束最大值和最小值

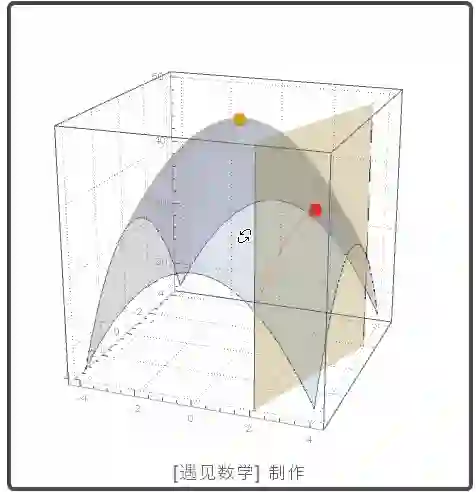
观察下面函数 f(x,y)=$\text{49-}{x}^2-y^2$ 受约束 g(x,y)=x+3y-10=0 的图形.

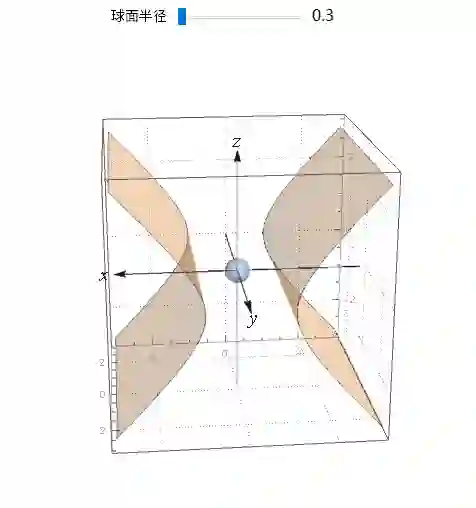
求双曲柱面 $x^2-z^2\text{-1=0}$ 上到原点最近的点的一个方法是设想中心在原点的球面不断膨胀, 直到刚刚接触到柱面. 此时柱面和球面有同样的切平面和法线.

Lagrange 乘子法

若函数 f(x,y,z) 的变量受约束 g(x,y,z)=0限制, 函数的极值可以用下面Lagrange乘子法求出.

现在看函数 f(x,y)= x y 在椭圆 $\frac{x^2}{8}+\frac{y^2}{2}\text{=1}$ 上的最大值和最小值, 现在看下解的几何解释. f(x,y)=x y 的等高线图是双曲线 x y=c , 如下:

从上图可是双曲线离开原点越远, f 的绝对值越大. 需要在约束条件下 - 椭圆 $x^2+4y^2\text{=8}$ 上使 f(x,y) 取极值点. 也就是刚刚与椭圆相切的双曲线会距离原点最远, 在这四个切点中, 双曲线的法线也是椭圆的法线. 观察下图动画, 可以看到黑色 "▽f"是 "▽g"的数值倍数.

带两个约束条件的 Lagrange 乘子法

如果是两个约束限制的可微函数求极值, 这里 g1(x,y,z)=0 和 g2(x,y,z)=0, 可微且梯度向量不平行. 可以通过引进两个 Lagrange乘子 λ 和 μ, 通过求解下面方程中的 x,y,z,λ,μ 值来求出极值点的位置:

曲面 g1=0 和 g2=0 通常会相交于一条曲线 C. 沿着这条曲线寻找 f 相对于曲线上其他值的极大值和极小值的点.

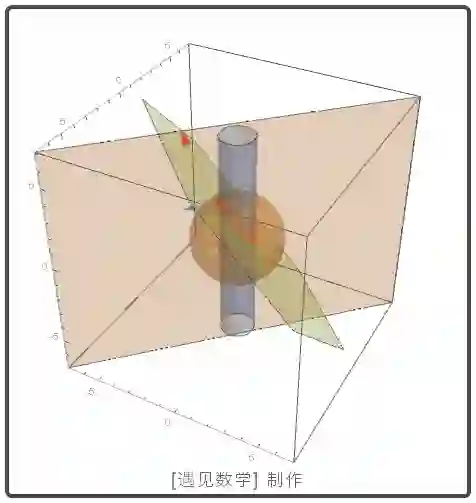
例如下面例子中平面 x+y+z=1 (g1)相交于圆柱 $x^2+y^2\text{=1}$ (g2) 为一个椭圆, 求这个椭圆上离原点最远的点. 观察 ▽g1 正交于平面 x+y+z=1, 而 ▽g2 正交于曲面$x^2+y^2\text{=1}$, 向量 ▽g1 和 ▽g2 位于垂直与椭圆曲线的 C (下图红色)的平面内. 并且 ▽f 也正交于 C, 且在 ▽g1 和 ▽g2 决定的平面内, 这意味这对于某个 λ 和 μ 有 ▽f = λ ▽g1 + μ ▽g2. 观察下图来更好理解: