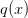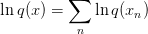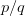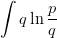学界 | Reddit一致好评的David Blei新作，其实有两大硬伤亟待斟酌

最近 David Blei 组提交了一篇论文《Deep and Hierarchical Implicit Models》，而此文也在 Reddit 上引起了不少讨论，而且呈现惊人的零差评。

为何 Blei 组的动态会如此快地受到关注？毕竟发文的三位个个皆非等闲之辈：

Dustin Tran 是哥伦比亚大学计算机科学博士生，师从 David Blei 和 Andrew Gelman。本科与硕士分别在伯克利大学及哈佛大学攻读。Tran 的主要关注方向包括贝叶斯统计、机器学习及深度学习。出于对概率模型的浓厚兴趣，Tran 搭建了 Edward，一个兼容 TF Slim 和 Keras 的概率编程库。

二作是普林斯顿大学的 Rajesh Ranganath，目前与 David Blei 共事。此前曾经与百度首席科学家吴恩达一同在斯坦福 AI 实验室研发深度学习，并与 Dan Jurafsky 一同在斯坦福 NLP 团队从事对话与社交动机的监测。

而 David Blei 自不必说，他是哥伦比亚大学的数据科学及计算机科学教授，主要关注机器学习及贝叶斯统计，研究领域包括主题模型、概率建模及近似贝叶斯推断。

在论文发布后，Dustin Tran 在博客上表示：

带着私心地评论，我认为这篇论文的想法简单，但影响却非常深刻。

举一个实用的例子，我们只需要将噪声输入隐藏层，就能够将任何的标准神经网络转换为一个深层的隐含模型。此外，诱导的潜变量呈现惊人的灵活性。没有比这更简单的深度生成模型了！

此外，Reddit 上也是好评一片：

• @fhuszar 认为，这篇文章将很多内容很好地整合在了一起。

  「今年的 ICML 有不少关于隐式模型变分推断的论文，但此论文大概是最具综合性兼实用性的一篇了。此外，论文中的一些例子是在 Edward 上搭建的（你说为啥偏要用 Edward？因为就是 Dustin Tran 一手开发的呀）。

  我最喜欢的部分是论文通过前向模型的全局参数进行概率处理和变分推断，而不是通过在 GAN 或 VAE 中完成 SGD 优化。总体而言，这使算法呈现一致性，并以相同的方式工作。」

• @heartastack 表示，看到是用 Edward 搭建的之后，「非常期待拜读一番。」

• @abojchevski 也发来贺电：「很棒的论文，继续加油！」

• @ bronzestick 则认为，这篇论文写得太好了。

然而，在 Reddit 上受到如此好评的这篇大作，是否真的名副其实呢？AI 科技评论联系上了在知乎上讨论该论文的两位知友，一位是商汤科技的陈默，另一位是来自中山大学的郑华滨。他们并不像 Reddit 用户一样全面赞美，而是提出了这篇论文的不少问题。

不过首先，AI 科技评论还得从显式概率模型（explicit probability model）与隐式概率模型（implicit probability model）开始说起。

在生成模型中，对概率分布一般的建模方式是所谓的显式概率模型，它能够写出一个显式的概率密度函数（density）或似然函数（likelihood）。

而隐式概率模型又该如何理解呢？我们可以用抛硬币来举例。研究者们都知道，硬币的正反面完全受物理学定律的控制（比如抛掷的角度和施加于硬币的压力），因此，硬币结果的随机性不是因潜在的概率，而会受到很多嘈杂初始参数的影响。这种模型结合了物理学，也能够更好地捕获生成过程。此外，该模型是隐式的（模拟器），研究者能够从生成过程中采样数据，但无法计算密度。

而这篇论文的最大亮点就在于它试图将层次概率模型和变分后验分布都建模成隐式概率模型，这是因为隐式概率模型只能从这个概率分布中采样，但是不要求能够计算某个样本的似然函数，被认为可以更好、更灵活地反映真实世界的物理过程。

然而，由于难以对隐式概率模型构建准确、可规模化的贝叶斯推断，所以以往的隐式概率模型用得并不多。为了解决这一问题，研究者受到比率估计的启发，设计了一种名为 LFVI（likelihood-free variational inference）的推断方式，作为该模型的近似求解算法。

研究者也在论文中提到，这项工作具有广泛的应用范围。具体包括：

1. 分析近似贝叶斯计算（ABC）的经典问题，采用传统方法无法驾驭的大规模数据；

2. 分析贝叶斯 GAN，它能够让 GANs 量化不确定性，并提升数据的有效性。

3. 分析深层隐含模型的文本与 RNN，能够推进大范围的隐式模型，并推进建模设计。

陈默在知乎上肯定了论文的创新性。在贝叶斯框架上对一个网络进行训练，通常手段是将网络转化为概率图模型的对应形式，再用贝叶斯的推断手段进行训练。「而这篇 paper 的思路，是我们不需要做这样的转化，只需要把给定 network 的每层作为一个 implicit function g，然后我们在每层加一个简单的 generate 项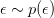，整个网络就是 probabilistic 的了。」

郑华滨在接受 AI 科技评论采访时也指出，论文采用了隐式建模的方法，认为这更能反映真实世界的情况。他在知乎上指出，「作者利用了一个名为 ratio estimation 的技术，通过直接对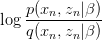 进行近似求值，进而计算梯度。」

但是，两位都认为这篇论文不论是从求解思路还是实用角度上，都有很多需要斟酌的地方。

陈默列出了一些疑问。首先是分解式的推导存在合理性问题：

• 对 marginal distribution，这个分解 是一定不成立的，所以我对 (5) 到 (6) 的合理性有疑问。

• 对于 (7) 的解貌似是近似的 density ratio:，而并不是 expectation:。

其次是近似解的合理性问题。

「论文中 GAN 的 target 近似解了 Bayesian lower bound，我觉得这个近似有点扯，并且太刻意。而恰恰用哪个分布对 log ratio 求期望才是 Bayesian 和 non Bayesian 的分界岭（对 p 求期望实际上就是 maximium likelihood，对 q 求期望是 Bayesian，而 GAN 是即对 p 求又对 q 求，两项加起来。实际上当样本无穷大时候，三个 estimator 都收敛到真实分布，可以说互相都是近似，但这个近似根本没啥意义。）虽然说，以上两点反正是近似，也不是很有所谓。但这样随意的近似对我来说实在是有点无厘头。」郑华滨在与陈默讨论之时，也赞同了推导过程有问题的观点。

此外在实用性上，双方都认为任重道远。在郑华滨看来，除了 VAE 等少数模型之外，目前还很少看贝叶斯深度学习这类研究在大数据集中奏效，而这篇论文也没有跳出这一桎梏，比如它的文本 GAN 实验也是在四则运算序列这种极度特定的数据上做的。不过他认为同样是四则运算序列，这篇论文相对于之前的 Gumbel-Softmax GAN 而言还是有所突破的。

陈默认为对贝叶斯方法持观望状态，认为目前还处于不实用阶段，还是得先解决推断算法的 underestimate 问题。「类似于 mean filed+sampling 的 inference 算法再怎么搞也很难走通，毕竟独立性 assumption 过强导致的 underestimate 是 fundamental problem，对于深度网络尤其严重，网络越复杂问题越严重，而 sampling 让近似有效性问题变的更严重，而且收敛速度必然很慢。」

AI 科技评论也将持续关注贝叶斯机器学习的研究进展，期待有一天能出现实验结果更好的推断算法。

AI科技评论招聘季全新启动！

很多读者在思考，“我和AI科技评论的距离在哪里？”，答案就是：一封求职信。

AI科技评论自创立以来，围绕学界和业界鳌头，一直为读者提供专业的AI学界，业界，开发者内容报道。我们与学术界一流专家保持密切联系，获得第一手学术进展；我们深入巨头公司AI实验室，洞悉最新产业变化；我们覆盖A类国际学术会议，发现和推动学术界和产业界的不断融合。

而你只要加入我们，就有机会和我们一起记录这个风起云涌的人工智能时代！

如果你有下面任何两项，请投简历给我们：

＊英语好，看论文毫无压力

＊计算机科学或者数学相关专业毕业，好钻研

＊新闻媒体相关专业，好社交

＊态度好，学习能力强

简历投递：lizongren@leiphone.com