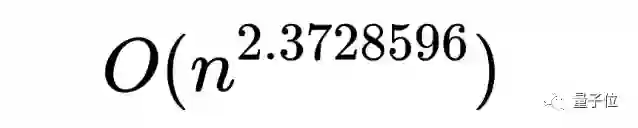AlphaTensor横空出世!打破矩阵乘法计算速度50年纪录,DeepMind新研究再刷Nature封面,详细算法已开源
羿阁 萧箫 发自 凹非寺
量子位 | 公众号 QbitAI
什么,AI竟然能自己改进矩阵乘法,提升计算速度了?!
还是直接打破人类50年前创下的最快纪录的那种。
要知道,矩阵乘法可是计算机科学中最基础的数学算法之一,也是各种AI计算方法的基石,如今计算机处理图像语音、压缩数据等全都离不开它。
但自从德国数学家沃尔克·施特拉森(Volker Strassen)在1969年提出“施特拉森算法”后,矩阵乘法的计算速度一直进步甚微。
现在,这只新出炉的AI不仅改进了目前最优的4×4矩阵解法(50年前由施特拉森提出),还进一步提升了其他70余种不同大小矩阵的计算速度。
这是DeepMind最新研究成果AlphaTensor,一经发出就登上了Nature封面。
有意思的是,AlphaTensor并非一开始就是专攻理论研究的,它的前身AlphaZero其实是个用来下下围棋、国际象棋的“棋类AI”。
这项研究发布后,一名在DeepMind工作6年的老员工表示:
我在DeepMind干了这么些年,能让我吃惊的东西确实不多了,但这项研究确实让我倒吸一口凉气。
前谷歌大脑工程师Eric Jang也激动转发:干得好!
那么,这只“游戏”AI究竟是怎么打破50年前人类创下的纪录的?
从最强棋类AI进化而来
AlphaTensor,从DeepMind的最强通用棋类AI“AlphaZero”进化而来。
所以,矩阵乘法和棋类有什么关系?
和棋盘一样,矩阵看起来也是方方正正的,每一格可以用对应的数据表示。
因此研究人员突发奇想,能不能直接把AI做矩阵乘法,当成是AI在棋盘上下棋?
其中棋盘代表要解决的乘法问题,下棋步骤代表解决问题的步骤,对应的规则被命名为TensorGame,一种新的“3D棋类游戏”。
但与棋类AI略有不同的是,AlphaZero要找到的是做矩阵乘法的最佳算法——即通过尽可能少的步骤,来“赢”得比赛,也就是计算出最终结果。
在了解AlphaTensor具体如何训练之前,先来简单回顾一下矩阵乘法的计算。
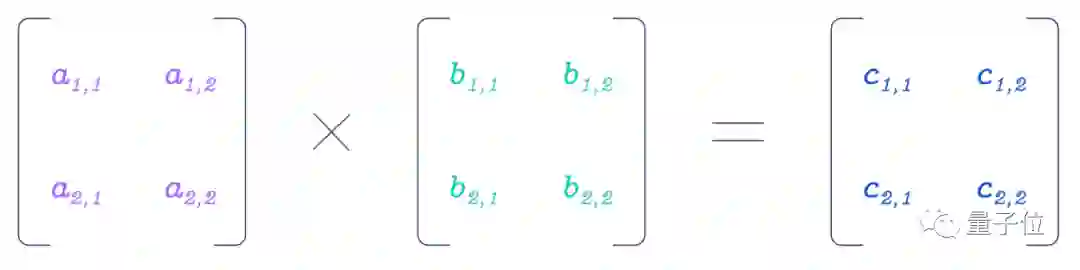
以计算最简单的2×2矩阵乘法为例:
正常来说,我们需要计算8次乘法,再通过4次加法来获得最终的结果:
但在矩阵乘法运算中,乘法的复杂度是O(n³),而加法的复杂度只有O(n²),n越大时此方法的收益就越大。
因此,如果能想办法降低做乘法的步骤,就能进一步加速矩阵乘法的运算速度。
例如根据经典的Strassen算法,两个2×2的矩阵相乘只需做7次乘法,时间复杂度也会进一步下降。
当然,这只是最简单的矩阵乘法之一。
对于更大、更复杂的矩阵乘法来说,计算出最终结果的可能性只会越来越多——
甚至对于两个矩阵相乘的方法来说,最终可能性比宇宙中的原子还要多(数量级达到10的33次方)。
与AlphaZero之前搞定的围棋游戏相比,AlphaTensor的计算量还要更大,因为矩阵乘法比围棋可能的步骤还要多出30倍左右。
它同样采用强化学习训练,并在训练之前先学习了一些人类计算矩阵乘法的方法,避免在过程中“无脑乱猜”,浪费不必要的计算量。
在训练时,AlphaTensor每一步都会从一个可选择的操作集(包含下一步可以做的所有计算动作)选择要完成的下一个动作,最终训练自己通过更少的步骤达成计算目标。
具体在选择的过程中,AlphaTensor采取了树搜索(Tree Search)的方法,即基于现有游戏结果预测下一个最可能降低步骤的动作。
出乎研究者们意料的是,AlphaTensor发现的计算矩阵乘法的方法真的挺有效。
例如在英伟达V100 GPU和谷歌TPU v2这两种硬件上,使用AlphaTensor发现的算法计算矩阵乘法,比常用算法要快上10~20%左右。
(当然研究者们也表示,其他处理器还得看硬件逻辑,计算方法不一定针对每个处理器都有这么好的加速作用)
具体而言,AlphaTensor一共改进了70多种不同大小矩阵的计算方法。
效率超越70+现有计算方法
矩阵乘法是计算机要做的最关键数学计算之一。
同时,它也是机器学习计算中不可或缺的基础,无论在AI处理手机图像、理解语音命令,还是渲染电脑游戏画面(计算机图形学)等方面,都能见到它的身影。
如今我们做矩阵乘法,很大程度上仍然离不开50年前的Strassen算法。
1969年,德国数学家沃尔克·施特拉森(Volker Strassen)证明,将两个2×2的矩阵相乘,不一定需要进行8次乘法。
他巧妙的通过构造7个中间变量,用增加14次加法为代价省去了一次乘法,这种方法被称为“施特拉森算法”(Strassen算法)。
基于Strassen算法逻辑,沃尔克·施特拉森改进了当时的一大批矩阵乘法。
50多年来,尽管针对一些不容易适应计算机代码的地方进行了轻微改进,但该算法一直是大多数矩阵大小上最有效的方法。
现在,AlphaTensor的出现刷新了这一纪录:
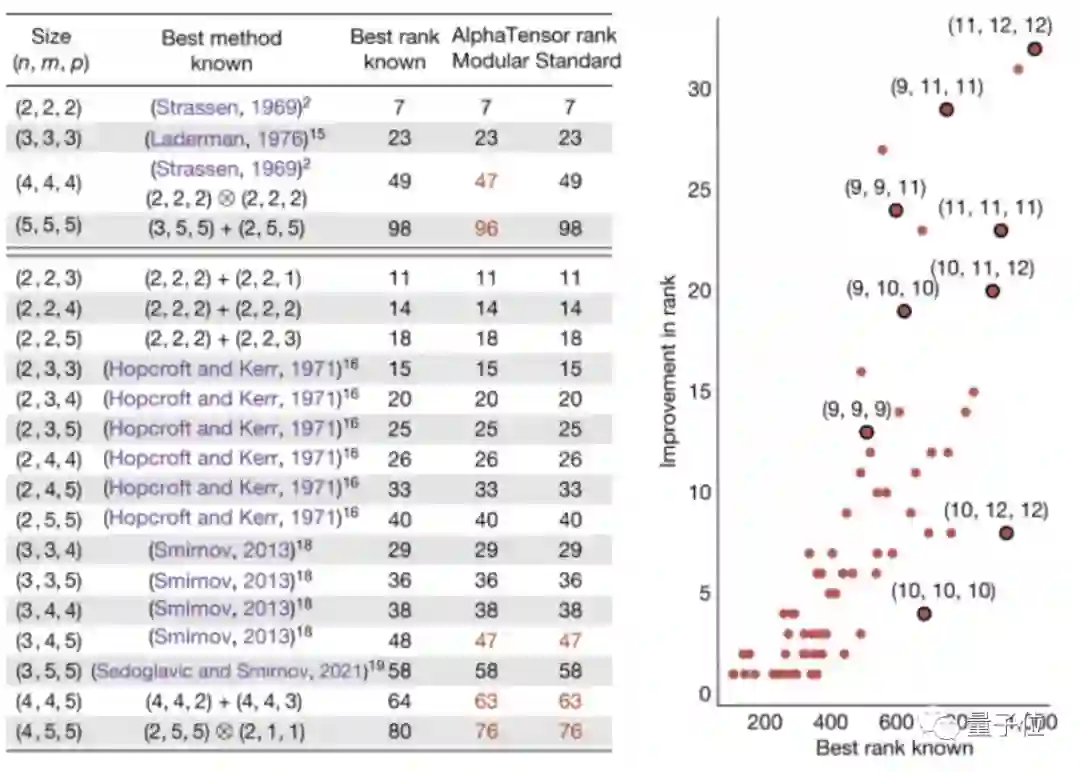
它发现了一种仅用47次乘法就能将两个4×4的矩阵相乘的算法,超过了施特拉森算法所需的49次乘法。
不仅如此,AlphaTensor还发现了比以前想象的更丰富的矩阵乘法算法空间——每种尺寸上多达数千个算法。
最终,它在70种不同大小矩阵的矩阵乘法中击败了现有的最佳算法。
举个例子,2个9×9矩阵相乘所需的步骤数从511步减少到498步,2个11×11矩阵相乘所需的步骤数从919步减少到896步……
所以在时间复杂度上,AlphaTensor是否做出了对应的突破?
对此论文介绍称,目前最优的矩阵乘法时间复杂度,仍然是2021年3月MIT&哈佛大学研究中达成的这一数值(AlphaTensor改善的时间复杂度并不比它更低)——
BUT,这个操作起来实在是太麻烦了,所以在实际计算中用处不大,除非计算的是天文数字大小的矩阵。
换而言之,即使Strassen算法的复杂度只达到O(n^2.81),但在大多数情况下,都要比上面那个时间复杂度更低的计算方法更实用。
嗯,更别提在不少特定矩阵乘法中还超过了Strassen算法的AlphaTensor了。
同时研究人员也表示,AlphaTensor设计的算法具有一定的灵活性。
它不仅可能推进各种应用程序重新设计算法,还可能优化能源使用量和数值稳定性等指标,帮助在实际应用时防止算法运行时出现小的舍入误差(包括Strassen算法等计算矩阵乘法,都会出现一定的误差)。
此外,虽然目前这些突破还只是针对特定算法改进的,但也有科学家认为AlphaTensor的潜力不止于此。
例如,MIT计算机科学家Virginia Williams就表示:
研究者们可以再尝试一下,去搞明白这些特定算法中有没有什么特殊规律。此外,也可以研究一下如果将这些特殊算法组合起来,是否能发现更多更优的计算方法。
目前AlphaTensor的相关代码已经开源。
共同一作也是AlphaGo关键“摆棋手”
AlphaTensor的研究团队都来自DeepMind。
5位共同一作分别是Alhussein Fawzi、Matej Balog、黄士杰、Thomas Hubert和Bernardino Romera-Paredes。
其中黄士杰来自中国台湾,本科毕业于台湾交通大学计算机与信息科学专业,在台湾师范大学获得研究生、博士学位,后前往加拿大阿尔伯塔大学攻读博士后,于2012年加入DeepMind。
他曾在AlphaGo和李世石大战中,担当AlphaGo的“人肉臂”(顺便把棋输入电脑),也是AlphaGo论文的共同一作。
对于这只AI达成的新成就,有网友调侃:
有意思的是,这只AI竟然是基于旧的矩阵乘法运算规则,算出这个新矩阵乘法计算方法的。
论文地址:
https://www.nature.com/articles/s41586-022-05172-4
参考链接:
[1]https://www.technologyreview.com/2022/10/05/1060717/deepmind-uses-its-game-playing-ai-to-best-a-50-year-old-record-in-computer-science/
[2]https://www.nature.com/articles/d41586-022-03166-w
[3]https://www.deepmind.com/blog/discovering-novel-algorithms-with-alphatensor
[4]https://twitter.com/DeepMind/status/1577677899108421633
— 完 —
「2022人工智能年度评选」火热报名中
现在,量子位「2022人工智能年度评选」已经正式启幕,评选将从企业、人物、产品/解决方案三大维度设置5类奖项。
更多关于评选标准、榜单报名欢迎扫描下方二维码~

点这里关注我 👇 记得标星噢 ~
一键三连「分享」、「点赞」和「在看」
科技前沿进展日日相见 ~