强化学习发现矩阵乘法算法,DeepMind再登Nature封面推出AlphaTensor
转载机器之心
DeepMind 的 Alpha 系列 AI 智能体家族又多了一个成员——AlphaTensor,这次是用来发现算法。
数千年来,算法一直在帮助数学家们进行基本运算。早在很久之前,古埃及人就发明了一种不需要乘法表就能将两个数字相乘的算法。希腊数学家欧几里得描述了一种计算最大公约数的算法,这种算法至今仍在使用。在伊斯兰的黄金时代,波斯数学家 Muhammad ibn Musa al-Khwarizmi 设计了一种求解线性方程和二次方程的新算法,这些算法都对后来的研究产生了深远的影响。
事实上,算法一词的出现,有这样一种说法:波斯数学家 Muhammad ibn Musa al-Khwarizmi 名字中的 al-Khwarizmi 一词翻译为拉丁语为 Algoritmi 的意思,从而引出了算法一词。不过,虽然今天我们对算法很熟悉,可以从课堂中学习、在科研领域也经常遇到,似乎整个社会都在使用算法,然而发现新算法的过程是非常困难的。
现在,DeepMind 用 AI 来发现新算法。
在最新一期 Nature 封面论文《Discovering faster matrix multiplication algorithms with reinforcement learning》中,DeepMind 提出了 AlphaTensor,并表示它是第一个可用于为矩阵乘法等基本任务发现新颖、高效且可证明正确的算法的人工智能系统。简单来说,使用 AlphaTensor 能够发现新算法。这项研究揭示了 50 年来在数学领域一个悬而未决的问题,即找到两个矩阵相乘最快方法。
论文地址 :https://www.nature.com/articles/s41586-022-05172-4
GitHub 地址:https://github.com/deepmind/alphatensor
AlphaTensor 建立在 AlphaZero 的基础上,而 AlphaZero 是一种在国际象棋、围棋和将棋等棋盘游戏中可以打败人类的智能体。这项工作展示了 AlphaZero 从用于游戏到首次用于解决未解决的数学问题的一次转变。
矩阵乘法
矩阵乘法是代数中最简单的运算之一,通常在高中数学课上教授。但在课堂之外,这种不起眼的数学运算在当代数字世界中产生了巨大的影响,在现代计算中无处不在。
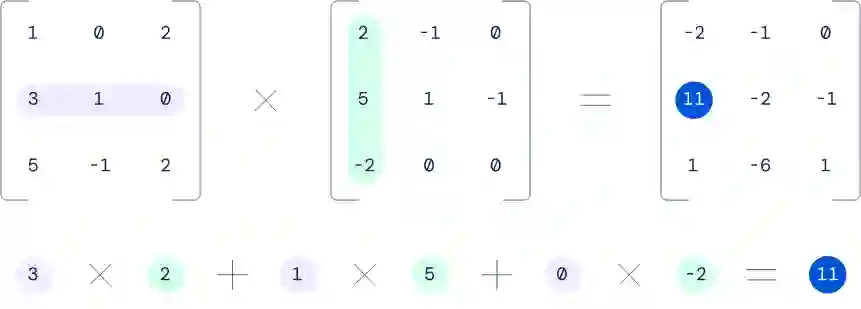
两个 3x3 矩阵相乘的例子。
你可能没注意到,我们生活中处处隐藏着矩阵相乘,如智能手机中的图像处理、识别语音命令、为电脑游戏生成图形等都有它在背后进行运算。遍布世界各地的公司都愿意花费大量的时间和金钱开发计算硬件以有效地解决矩阵相乘。因此,即使是对矩阵乘法效率的微小改进也会产生广泛的影响。
几个世纪以来,数学家认为标准矩阵乘法算法是效率最高的算法。但在 1969 年,德国数学家 Volken Strassen 通过证明确实存在更好的算法,这一研究震惊了整个数学界。
标准算法与 Strassen 算法对比,后者少进行了一次乘法运算,为 7 次,而前者需要 8 次,整体效率大幅提高。
通过研究非常小的矩阵(大小为 2x2),Strassen 发现了一种巧妙的方法来组合矩阵的项以产生更快的算法。之后数十年,研究者都在研究更大的矩阵,甚至找到 3x3 矩阵相乘的高效方法,都还没有解决。
DeepMind 的最新研究探讨了现代 AI 技术如何推动新矩阵乘法算法的自动发现。基于人类直觉(human intuition)的进步,对于更大的矩阵来说,AlphaTensor 发现的算法比许多 SOTA 方法更有效。该研究表明 AI 设计的算法优于人类设计的算法,这是算法发现领域向前迈出的重要一步。
算法发现自动化的过程和进展
首先将发现矩阵乘法高效算法的问题转换为单人游戏。其中,board 是一个三维度张量(数字数组),用于捕捉当前算法的正确程度。通过一组与算法指令相对应的所允许的移动,玩家尝试修改张量并将其条目归零。
当玩家设法这样做时,将为任何一对矩阵生成可证明是正确的矩阵乘法算法,并且其效率由将张量清零所采取的步骤数来衡量。
这个游戏非常具有挑战性,要考虑的可能算法的数量远远大于宇宙中原子的数量,即使对于矩阵乘法这样小的情况也是如此。与几十年来一直是人工智能挑战的围棋游戏相比,该游戏每一步可能的移动数量要多 30 个数量级(DeepMind 考虑的一种设置是 10^33 以上。)
为了解决这个与传统游戏明显不同的领域所面临的挑战,DeepMind 开发了多个关键组件,包括一个结合特定问题归纳偏置的全新神经网络架构、一个生成有用合成数据的程序以及一种利用问题对称性的方法。
接着,DeepMind 训练了一个利用强化学习的智能体 AlphaTensor 来玩这个游戏,该智能体在开始时没有任何现有矩阵乘法算法的知识。通过学习,AlphaTensor 随时间逐渐地改进,重新发现了历史上的快速矩阵算法(如 Strassen 算法),并且发现算法的速度比以往已知的要快。
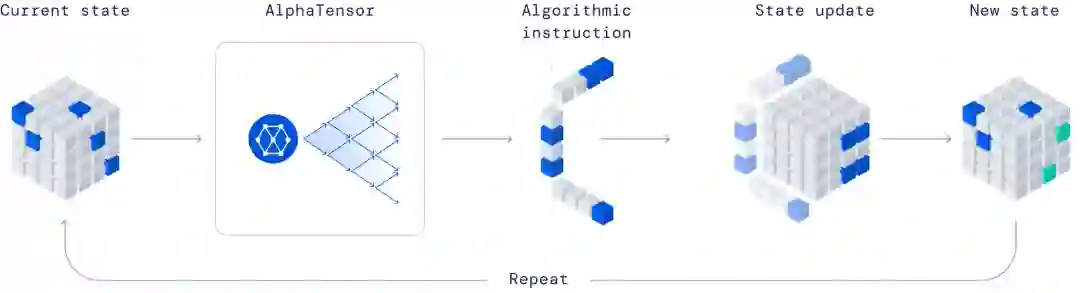
AlphaTensor 玩的单人游戏,目标是找到正确的矩阵乘法算法。游戏状态是一个由数字组成的立方数组(灰色表示 0,蓝色表示 1,绿色表示 - 1),它代表了要完成的剩余工作。
举例而言,如果学校里教的传统算法可以使用 100 次乘法完成 4x5 与 5x5 矩阵相乘,通过人类的聪明才智可以将这一数字降至 80 次。与之相比,AlphaTensor 发现的算法只需使用 76 次乘法即可完成相同的运算,如下图所示。
除了上述例子之外,AlphaTensor 发现的算法还首次在一个有限域中改进了 Strassen 的二阶算法。这些用于小矩阵相乘的算法可以当做原语来乘以任意大小的更大矩阵。
AlphaTensor 还发现了具有 SOTA 复杂性的多样化算法集,其中每种大小的矩阵乘法算法多达数千,表明矩阵乘法算法的空间比以前想象的要丰富。
在这个丰富空间中的算法具有不同的数学和实用属性。利用这种多样性,DeepMind 对 AlphaTensor 进行了调整,以专门发现在给定硬件(如 Nvidia V100 GPU、Google TPU v2)上运行速度快的算法。这些算法在相同硬件上进行大矩阵相乘的速度比常用算法快了 10-20%,表明了 AlphaTensor 在优化任意目标方面具备了灵活性。
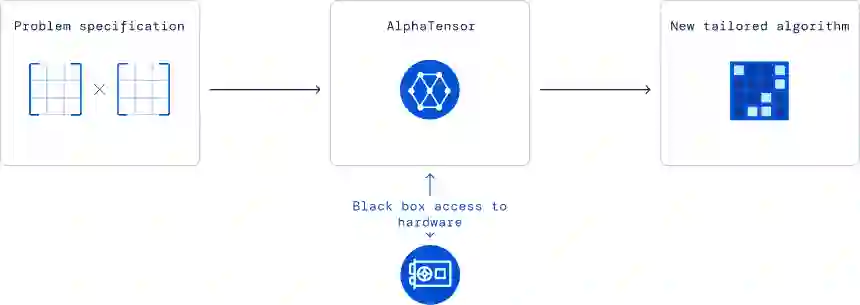
AlphaTensor 具有一个对应于算法运行时的目标。当发现正确的矩阵乘法算法时,它会在指定硬件上进行基准测试,然后反馈给 AlphaTensor,以便在指定硬件上学习更高效的算法。
对未来研究和应用的影响
从数学的角度来看,对于旨在确定解决计算问题的最快算法的复杂性理论而言,DeepMind 的结果可以指导它的进一步研究。通过较以往方法更高效地探索可能的算法空间,AlphaTensor 有助于加深我们对矩阵乘法算法丰富性的理解。
此外,由于矩阵乘法是计算机图形学、数字通信、神经网络训练和科学计算等很多计算任务的核心组成部分,AlphaTensor 发现的算法可以显著提升这些领域的计算效率。
虽然本文只专注于矩阵乘法这一特定问题,但 DeepMind 希望能够启发更多的人使用 AI 来指导其他基础计算任务的算法发现。并且,DeepMind 的研究还表明,AlphaZero 这种强大的算法远远超出了传统游戏的领域,可以帮助解决数学领域的开放问题。
未来,DeepMind 希望基于他们的研究,更多地将人工智能用来帮助社会解决数学和科学领域的一些最重要的挑战。
原文链接:https://www.deepmind.com/blog/discovering-novel-algorithms-with-alphatensor
专知便捷查看
便捷下载,请关注专知公众号(点击上方蓝色专知关注)
后台回复“ALTS” 就可以获取《强化学习发现矩阵乘法算法,DeepMind再登Nature封面推出AlphaTensor》专知下载链接