简明手册 | 附录：强化学习简介（二）

2020 年 5 月 9 日 TensorFlow

文 / 李锡涵，Google Developers Expert

本文节选自《简单粗暴 TensorFlow 2》，回复 “手册” 获取合集

从直接算法到迭代算法

到目前为止，我们都非常严格地遵循了动态规划中 “划分阶段” 的思想，即按照问题的时间特征将问题分成若干个阶段并依次求解。对应到数字三角形问题中，即从下到上逐层计算和更新未来期望（或 q 值），每一轮迭代中更新本层的未来期望（或 q 值）。在这个过程中，我们很确定，经过 N 次策略评估和策略改进后，算法将停止，而我们可以获得精确的最大数字和和最优动作。我们将这种算法称为 “直接算法”，这也是我们在各种算法竞赛中常见的算法类型。

不过在实际场景中，算法的计算时间往往是有限的，因此我们可能需要算法具有较好的 “渐进特性”，即并不要求算法输出精确的理论最优解，只需能够输出近似的较优解，且解的质量随着迭代次数的增加而提升。我们往往称这种算法为 “迭代算法”。对于数字三角形问题，我们考虑以下变式：

数字三角形问题（变式 3）
智能体初始在三角形的顶端，每次可以选择向下（）或者向右（）的动作。环境会对处于任意坐标 (i, j) 的智能体的动作产生“干扰”，而且这个干扰的具体概率未知。允许在数字三角形的环境中进行 K 次试验（K 可能很小也可能很大）。请设计试验方案和流程，确定智能体在每个坐标所应该选择的动作，使得智能体经过的路径上的数字之和的期望尽可能大。

为了解决这个问题，我们不妨从更高的层次来审视我们目前的算法做了什么。其实算法的主体是交替进行 “策略评估” 和 “策略改进” 两个步骤。其中，

“策略评估”根据智能体在坐标 (i, j) 的动作，评估在这套动作组合下，智能体在坐标 (i, j) 选择动作a的未来期望。
“策略改进”根据上一步计算出的，选择未来期望最大的动作来更新动作。

事实上，这一 “策略评估” 和 “策略改进” 的交替步骤并不一定需要按照层的顺序自下而上进行。我们只要确保算法能根据有限的试验结果 “尽量” 反复进行策略评估和策略改进，就能让算法输出的结果 “渐进” 地越变越好。于是，我们考虑以下算法流程：

初始化和；
repeat

固定智能体的动作的取值，进行 k 次试验（试验时加入一些随机扰动，使得能“探索”更多动作组合，上节也有类似操作）。
（策略评估）根据当前 k 次试验的结果，调整智能体的未来期望的取值，使得的取值“尽量”能够真实反映智能体在当前动作下的未来期望（上节是精确调整 [4] 至等于未来期望）。
（策略改进）根据当前的值，选择未来期望较大的动作作为的取值。

until 所有坐标的 q 值都不再变化，或总试验次数大于 K

为了理解这个算法，我们不妨考虑一种极端情况：假设每轮迭代的试验次数k的值足够大，则策略评估步骤中可以将精确调整为完全等于智能体在当前动作下的未来期望，事实上就变成了上节算法的“粗放版”（上节的算法每次只更新一层的值为精确的未来期望，这里每次都更新了所有的值。在结果上没有差别，只是多了一些冗余计算）。

上面的算法只是一个大致的框架介绍。为了具体实现算法，我们接下来需要讨论两个问题：一是如何根据k次试验的结果更新智能体的未来期望，二是如何在试验时加入随机的探索机制。

q 值的渐进性更新

当每轮迭代的试验次数 k 足够大、覆盖的情形足够广，以至于每个坐标 (i, j) 和动作 a 的组合都有足够多的数据的时候，q 值的更新很简单：根据试验结果为每个 (i, j, a) 重新计算一个新的，并替换原有数值即可。

可是现在，我们一共只有较少的k次试验结果（例如 5 次或 10 次）。尽管这 k 次试验是基于当前最新的动作方案来实施的，可一是次数太少统计效应不明显，二是原来的 q 值也不见得那么不靠谱（毕竟每次迭代并不见得会把更改太多）。于是，相比于根据试验结果直接计算一个新的 q 值并覆盖原有值（我们在前面的直接算法里一直都是这样做的 [5] ）：

(5)

一个更聪明的方法是“渐进”地更新 q 值。也就是说，我们把旧的 q 值向当前试验的结果稍微“牵引”一点，作为新的 q 值，从而让新的 q 值更贴近当前试验的结果，即 (6)

其中参数控制牵引的“力度”（牵引力度为 1 时，就退化为了使用试验结果直接覆盖 q 值的 (5) 式，不过我们一般会设一个小一点的数字，比如 0.1 或 0.01）。通过这种方式，我们既加入了新的试验所带来的信息，又保留了部分旧的知识。其实很多迭代算法都有类似的特点。

不过，的值只有当一次试验完全做完的时候才能获得。也就是说，只有走到了数字三角形的最底层，才能知道路径途中的每个坐标到路径最底端的数字之和（从而更新路径途中的所有坐标的 q 值）。这在有些场景会造成效率的低下，所以我们在实际更新时往往使用另一种方法，使得我们每走一步都可以更新一次q值。具体地说，假设某一次试验中我们在数字三角形的坐标(i, j)处，通过执行动作（代表加上一些探索扰动）而跳到了坐标(i',j')（即“走一步”，可能是(i+1, j)，也可能是(i+1, j+1)），然后又在坐标(i',j')执行了动作。这时我们可以用来近似替代之前的，如下式所示： (7)

我们甚至可以不需要试验结果中的，而使用在坐标(i', j')时两个动作对应的q值的较大者来代替，如下式： (8)

探索策略

对于我们前面介绍的，基于试验的算法而言，由于环境里的概率参数是未知的（类似于将环境看做黑盒），所以我们在试验时一般都需要加入一些随机的“探索策略”，以保证试验的结果能覆盖到比较多的情况。否则的话，由于智能体在每个坐标都具有固定的动作，所以试验的结果会受到极大的限制，导致陷入局部最优的情况。考虑最极端的情况，假若我们回到本节之初的原版数字三角形问题（环境确定、已知且不受概率影响），当动作也固定时，无论进行多少次试验，结果都是完全固定且唯一的，使得我们没有任何改进和优化的空间。

探索的策略有很多种，在此我们介绍一种较为简单的方法：设定一个概率比例，以的概率随机生成动作（或），以的概率选择动作。我们可以看到，当时，相当于完全随机地选取动作。当时，则相当于没有加入任何随机扰动，直接选择动作。一般而言，在迭代初始的时候的取值较大，以扩大探索的范围。随着迭代次数的增加，的值逐渐变优，的取值会逐渐减小。

大规模问题的求解

算法设计有两个永恒的指标：时间和空间。通过将直接算法改造为迭代算法，我们初步解决了算法在时间消耗上的问题。于是我们的下一个挑战就是空间消耗，这主要体现在 q 值的存储上。在前面的描述中，我们不断迭代更新的值。这默认了我们在内存中建立了一个的三维数组，可以记录并不断更新 q 值。然而，假若 N 很大，而计算机的内存空间又很有限，那我们该怎么办呢？

我们来思考一下，当我们具体实现时，我们需要其能够实现的功能有二：

q 值映射：给定坐标 (i, j) 和动作 a（或），可以输出一个值。
q 值更新：给定坐标 (i, j)、动作 a 和目标值 target，可以更新 q 值映射，使得更新后输出的距离目标值 target 更近。

事实上，我们有不少近似方法，可以让我们在不使用太多内存的情况下实现一个满足以上两个功能的。这里介绍一种最流行的方法，即使用深度神经网络近似实现：

q 值映射：将坐标 (i, j) 输入深度神经网络，网络输出在坐标 (i, j) 下的所有动作的 q 值（即和）。
q 值更新：给定坐标 (i, j)、动作 a 和目标值 target，将坐标 (i, j) 输入深度神经网络，网络输出在坐标 (i, j) 下的所有动作的 q 值，取其中动作为 a 的 q 值为，并定义损失函数，使用优化器（例如梯度下降）对该损失函数进行一步优化。此处优化器的步长和上文中的“牵引参数” 作用类似。

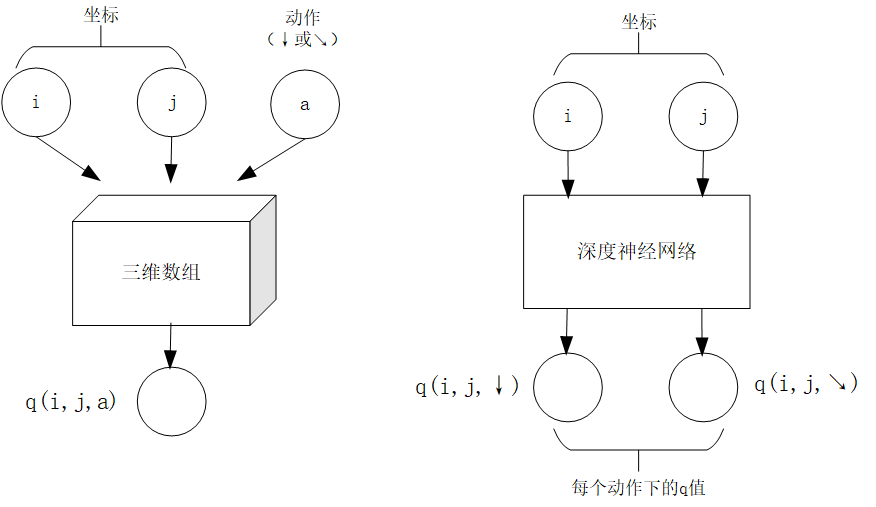
对于数字三角形问题，左图为使用三维数组实现，右图为使用深度神经网络近似实现

总结

尽管我们在前文中并未提及 “强化学习” 一词，但其实我们在对数字三角形问题各种变式的讨论中，已经涉及了很多强化学习的基本概念及算法，在此列举：

在第二节中，我们讨论了基于模型的强化学习（Model-based Reinforcement Learning），包括值迭代（Value Iteration）和策略迭代（Policy Iteration）两种方法。
在第三节中，我们讨论了无模型的强化学习（Model-free Reinforcement Learning）。
在第四节中，我们讨论了蒙特卡罗方法（Monte-Carlo Method）和时间差分法（Temporial-Difference Method），以及 SARSA 和 Q-learning 两种学习方法。
在第五节中，我们讨论了使用 Q 网络（Q-Network）近似实现 Q 函数来进行深度强化学习（Deep Reinforcement Learning）。

其中部分术语对应关系如下：

数字三角形的坐标 (i, j) 被称为状态（State），用表示。状态的集合用表示。
智能体的两种动作和被称为动作（Action），用表示。动作的集合用表示。数字三角形在每个坐标的数字被称为奖励（Reward），用（只与状态有关）或（与状态和动作均有关）表示。奖励的集合用表示。
数字三角形环境中的概率参数和被称为状态转移概率（State Transition Probabilities），用一个三参数函数表示，代表在状态 s 进行动作 a 到达状态 s' 的概率。
状态、动作、奖励、状态转移概率，外加一个时间折扣系数的五元组构成一个马尔可夫决策过程（Markov Decision Process，简称MDP）。数字三角形问题中。
第二节中 MDP 已知的强化学习称为基于模型的强化学习，第三节 MDP 的状态转移概率未知的强化学习称为无模型的强化学习。
智能体在每个坐标 (i, j) 处会选择的动作被称为策略（Policy），用表示。智能体的最优策略用表示。
第二节中，当策略一定时，智能体在坐标(i, j)处 “现在及未来将会获得的数字之和的期望” 被称为状态-价值函数（State-Value Function），用表示。智能体在坐标 (i, j) 处“未来将会获得的数字之和的期望的最大值” 被称为最优策略下的状态—价值函数，用表示。
第三节中，当策略一定时，智能体在坐标 (i, j) 处选择动作 a 时 “现在及未来将会获得的数字之和的期望” 被称为动作—价值函数（Action-Value Function），用表示。最优策略下的状态-价值函数用表示。
在第三节和第四节中，使用试验结果直接取均值估计的方法，称为蒙特卡罗方法。(7) 中用来近似替代的的方法称为时间差分法， (7) 的 q 值更新方法本身称为 SARSA 方法。(8) 称之为 Q-learning 方法。

推荐阅读
如果读者希望进一步理解强化学习相关知识，可以参考
- SJTU Multi-Agent Reinforcement Learning Tutorial http://wnzhang.net/tutorials/marl2018/index.html （简明的强化学习入门幻灯片）
- 强化学习知识大讲堂 https://zhuanlan.zhihu.com/sharerl （内容广泛的中文强化学习专栏）
- 郭宪, 方勇纯. 深入浅出强化学习：原理入门. 电子工业出版社, 2018. （较为通俗易懂的中文强化学习入门教程）
- Richard S. Sutton, Andrew G. Barto. 强化学习（第二版）. 电子工业出版社, 2019. （较为系统理论的经典强化学习教材）

[1] 所以有时又被称为 “记忆化搜索”，或者说记忆化搜索是动态规划的一种具体实现形式。

[2] 期望是试验中每次可能结果的概率乘以其结果的总和，反映了随机变量平均取值的大小。例如，你在一次投资中有的概率赚 100 元，有的概率赚 200 元，则你本次投资赚取金额的期望为元。也就是说，如果你重复这项投资多次，则所获收益的平均值趋近于 175 元。

[3] 作为参考，在前节中，

[4] 这里和下文中的 “精确” 都是相对于迭代算法的有限次试验而言的。只要是基于试验的方法，所获得的期望都是估计值。

[5] 不过在这里，如果我们在迭代第一步的试验时加入了随机扰动的 “探索策略” 的话，这样计算是不太对的。因为 k 次试验结果受到了探索策略的影响，导致我们所评估的其实是随机扰动后的动作，使得我们根据试验结果统计出的存在偏差。为了解决这个问题，我们有两种方法。第一种方法是把随机扰动的 “探索策略” 加到第三步策略改进选择最大期望的过程里，第二种则需要采用一种叫做 “重要度采样”（Importance Sampling）的方法。由于我们真实采用的 q 值更新方法多是后面介绍的时间差分方法，所以这里省略关于重要度采样的介绍，有需要的读者可参考文末列出的强化学习相关文献进行了解。

如果本文有任何尚未详细解释的内容或者知识点，欢迎在这里 https://discuss.tf.wiki/ 提出并共同探讨。

《简单粗暴 TensorFlow 2》目录