【笔记】探索简单孪生网络表示学习

点击上方，选择星标或置顶，每天给你送干货 ！

阅读大概需要10分钟

跟随小博主，每天进步一丢丢

每日英文

You can nearly always enjoy something if you make up your mind firmly that you will.

只要你下定决心做某件事，总能从中找到乐趣。

Recommender：王萌

作者：StayGold

链接：https://zhuanlan.zhihu.com/p/321642265

编辑：王萌 (深度学习自然语言处理公众号)

论文

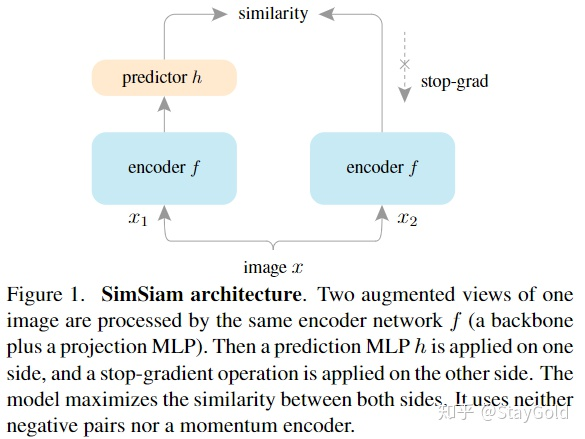
题目：Exploring Simple Siamese Representation Learning

来源：arXiv

原文链接：https://arxiv.org/pdf/2011.10566.pdf

来自：学习NLP的皮皮虾

Abstract

孪生网络的结构是无监督图像表示学习中的一个通用的结构，通过最大化同一个图像两个增强版本的相似度，同时通过一些方法来避免坍缩（collapsing）的问题。本文通过实验结果证明了即使是最简单的孪生网络也可以用于图像表示无监督预训练，并取得较好的效果。相比于其它工作，本文证明了以下组件是不必要的：

• 图像负样本对；

• 很大的batch size；

• 动量编码器

根据实验结果，确实发现了坍缩到固定表示的问题，但通过一个stop-gradient的操作能有效避免坍缩。随后本文还提出了一个假设来解释stop-gradient的效果，并通过实验验证了该假设。本文的简单方法（孪生网络+stop-gradient）在图像无监督表示学习上能取得和目前SOTA相近的效果。

Introduction

近一年出现了许多无监督、自监督图像表示学习的工作（MoCo、SimCLR、SwAV、BYOL等）。尽管它们的出发点、创新点各有不同，但大部分模型都遵从孪生网络的框架。即通过一个共享的编码器网络对同一个图像的不同增强版本（两个或多个）编码，使得它们具有较高的相似度。孪生网络是比较实体之间相似度的一个非常自然的工具。

但是，如果只是简单的最大化相似样本编码后的距离，孪生网络的输出会坍缩到某个固定常量。在这种情况下，网络输出的所有的表征都近似相同，因此损失降到最低，但准确率近乎为零。目前有一些策略来避免这一点，比如：

• 对比学习通过引入负样本，使得模型在最大化相同图像的相似度的同时，也得和负样本远离；

• SwAV引入聚类的目标，达到类似的效果；

• BYOL只包含正样本，但使用了动量编码器。

本文证明了即使没有上面三个策略，简单的孪生网络（称为SimSiam）也能达到类似的效果，只需要一个stop-gradient的操作。

作者认为，孪生网络很可能是目前的相关工作能够成功的关键因素，因为它从模型结构上引入了建模“不变性（invariance）”的归纳偏差（inductive bias）。

Method

本文的结构很简单，包含：

• 一个参数共享的编码器  ，通过ResNet实现；

• 一个非线性映射网络  ，通过MLP实现，称为predictor；

• stop-gradient操作，放在没有predictor的另一侧；

首先随机采样图像  的两个增强版本  和  ；随后，通过两侧的网络分别对其进行编码：  、  ；最后，将两个向量归一化后，最小化下面的负余弦距离损失：

进一步可以定义出对称的版本： 

上面损失的最小值就是 -1。

一个非常重要的、能让模型work的操作是stop-gradient操作，作者使用  来表示这一操作，这样，上面的两个损失分别变成了：

 

算法的伪代码如下：

Baseline设置：

• 优化器默认使用SGD，学习率根据batch_size缩放，256时为0.05；学习率通过cosine衰减，weight decay为0.0001；SGD动量设为0.9；

• 预测MLP为两层，中间层包含BN，维度为512，输入输出维度为2048；

Empirical Study

1. Stop-gradient的作用

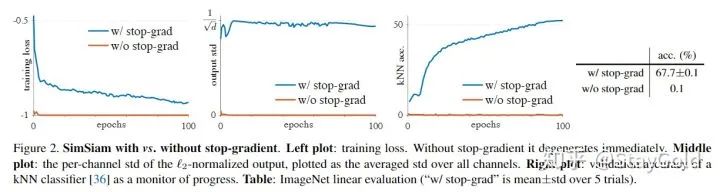
• 图左呈现了训练损失，如果没有stop-grad，损失很快到达0；而使用stop-grad的话，损失在不断下降；

• 第二张图显示了输出表示的方差，如果没有stop-grad，方差近乎为0（发生了坍缩）；而使用stop-grad能让方差为  ，差不多就是表示均匀分散在  维空间的单位超球平面上；

• 第三张图展示了KNN分类的准确率，可以看到没有stop-grad的话，KNN的准确率近乎为0；若加上stop-grad，则准确率随训练稳定上升。

2. Predictor的作用

为了验证Predictor的效果，作者对比了三种变体：

• 去掉Predictor：发生了坍缩（从训练公式上就可以推出来，和不包含stop-grad的设定等价了）；

• 随机初始化Predictor并固定：模型无法收敛，损失很高；

• Predictor部分的learning rate不衰减：获得了更高的结果。

3. Batch Size的影响

上图验证了batch size的影响，在256和512上获得了最好的效果，过大的batch size反而会损害性能，显示了本方法不依赖于过大的batch size。

4. Batch Normalization

上图验证了BN的效果，实验证明在projection（ResNet内）网络中的隐层和输出层，在predictor网络中的隐层加BN效果最好。

5. Similarity Function

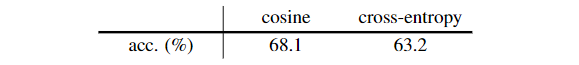
这里验证了损失函数的比较。其它所有因素保持一致。实验证明了对于cross-entropy也能work，证明了坍缩现象和损失函数无关。

6. Symmetrization

这里通过消融分析，说明了使用对称还是不对称的损失函数（3或4式）并不影响模型的收敛情况。作者倾向于认为对称的版本加强了数据，因此做了一个非对称（2x）的实验，发现能在1x的基础上进一步提升。

Hypothesis

基于上面的实验结果，本文提出了一个假设，来解释SimSiam隐式优化的目标。作者认为SimSiam类似于EM（Expectation-Maximization）算法，它隐式地和两组参数相关联，并通过一种迭代的方式分别优化这两组参数。stop-gradient存在的作用就是引入第二组可优化参数。

考虑如下的损失函数形式：

这里的  表示图像增强操作。这里引入了第二个可优化变量，即  。这里的  表示索引，即通过图像  找到对应的那个  ，它不再必须是神经网络的输出，而需要将其看作是优化问题中的一个参数。优化目标就是： 

这里的优化目标同时和  和  关联，就和k-means有点相似。在k-means中，也有两组需要优化的参数：一组是聚类中心（k个类别的聚类中心），这类似于优化目标中的  ；另一组是“每个样本分别属于哪个聚类”，这就类似于上面优化目标中的  （即对于每一张增强的图像都有一个与之对应的表征）。k-means算法中，优化上面两组参数是迭代进行的，即交替地计算每个类别的聚类中心，随后计算每个样本的聚类所属情况，直到训练稳定。上面的优化目标也类似，迭代进行以下两步： 

 

上面公式中，  代表迭代到了第几次，  表示赋值操作。

优化(7)式时，就使用神经网络梯度回传、更新；优化(8)式时，就使用如下的重新计算、赋值更新操作：

 

上式显示了，  的更新是通过计算不同增强版本的图像  的表示期望来得到的。

作者认为，SimSiam实际上模拟了上面(7)、(8)式的一步更新操作，只不过公式(9)中的采样只做一次：

 

将其代入公式(7)的子优化问题，得到：

 

上面的公式其实就是SimSiam的结构加上stop-gradient操作。

Predictor

作者接下来阐述了引入predictor  的目的。根据定义，期望最小化  。最优的  需要满足  。在公式(10)的优化中，因为只采样一次，期望  被忽略了，而引入  就可能通过神经网络的拟合能力去学习“预测期望”。

Proof of concept

作者构造了两个实验用来证明上述假设的正确性：

• 在同一个迭代内（公式(7), (8)），执行多步的SGD更新；

• 将Predictor去掉，然后通过一个滑动平均作为优化  的手段。

对于第一个实验，发现在同一个迭代内更新多步SGD能进一步提升性能：

对于第二个实验，发现去掉  ，引入滑动平均更新后，模型也能取得55%的准确率，和上面的表只取得0.1的准确率相比，说明了上述假设大致是正确的。

Comparisons

1. ImageNet

在ImageNet linear evaluation上，与目前SOTA的无监督表示学习方法对比：

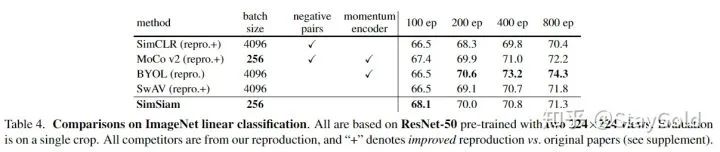
本文的方法在100 epoches的时候达到了最优效果，尽管随着epoch数增加，逐渐落后于其它方法。同时相比SimCLR，在任何epoch数的情况下均有提升。

2. Transfer Learning

在目标检测任务上迁移，发现本文的方法对比其它方法也是有竞争力的：

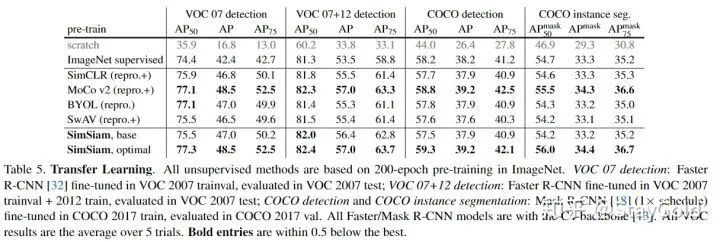
3. 与其他方法的对比：

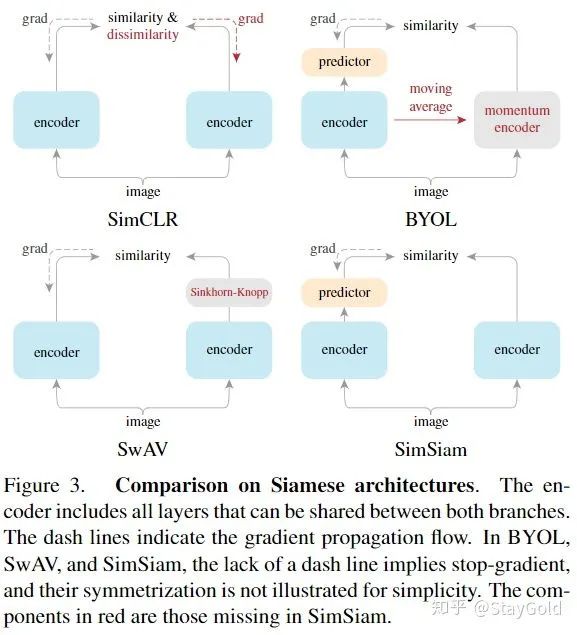
上图比较了目前的一些无监督图像表示预训练的方法，本文的SimSiam可以视为是公共结构，是其它方法减去某些组件后的共同的结构。

与SimCLR对比

SimSiam可以视为是SimCLR去掉负样本。为了进一步对比，作者对SimCLR加上了predictor和stop-grad结构，效果没有提升：

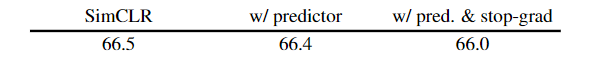
与SwAV对比

SimSiam可以视为SwAV去掉online clustering。作者同样对SwAV做了一些对比：

加入predictor依然没有提升，同时去掉stop-grad之后导致模型无法收敛。

与BYOL对比

SimSiam可以视为是BYOL去掉了动量编码器。如上面所说，公式(8)也可以通过其它优化器来优化，例如基于梯度的优化器（而不是简单赋值）。这会导致  相对平滑地更新。动量编码器也类似地起到了这种效果，因此BYOL效果较好。作者认为公式(8)的其它优化方法可以作为未来的研究方向。

说个正事哈

由于微信平台算法改版，公号内容将不再以时间排序展示，如果大家想第一时间看到我们的推送，强烈建议星标我们和给我们多点点【在看】。星标具体步骤为：

（1）点击页面 最上方 “ 深度学习自然语言处理 ”，进入公众号主页。

（2）点击 右上角的小点点 ，在弹出页面点击“ 设为星标 ”，就可以啦。

感谢支持，比心 。

投稿或交流学习，备注： 昵称-学校（公司）-方向，进入DL&NLP交流群。

方向有很多： 机器学习、深度学习，python，情感分析、意见挖掘、句法分析、机器翻译、人机对话、知识图谱、语音识别等。

记得备注呦

推荐两个专辑给大家：

专辑 | 李宏毅人类语言处理2020笔记

专辑 | NLP论文解读

专辑 | 情感分析

整理不易，还望给个在看！