最强大的GNN出现了!
本文介绍斯坦福 Jure Leskovec 组近日发表在 arXiv 上的最新工作
ヽ(✿゚▽゚)ノ 距离编码-为结构表示学习设计更强大的GNN.
Distance Encoding – Design Provably More Powerful GNNs for Structural Representation Learning

代码:https://github.com/snap-stanford/distance-encoding
摘要
从图结构数据中学习节点集的结构表示对于从节点角色发现到链接预测和分子分类的各种应用至关重要。图神经网络(GNNs)在结构表示学习方面取得了巨大的成功。然而:
-
大多数 GNN 受到 1-Weisfeiler-Lehman(WL)test 的限制,因此 有可能为实际上不同的结构和图形生成相同的表示。 -
最近通过模仿高阶 WL tests 提出的更强大的 GNN 只关注全图表示,不能利用图结构的稀疏性来提高计算效率。
这篇文章提出了一类与结构相关的特征,称为距离编码(Distance Encoding,DE),以帮助 GNN 以比 1-WL test 更严格的表达能力来表示任意大小的节点集。DE 本质上捕获了要学习表示的节点集与图中每个节点之间的距离,其中包括与图相关的重要度量,如最短路径距离和广义 PageRank 得分。
此外,此文还提出了两个通用的 GNNs 框架来使用 DEs:
-
作为额外的节点属性 -
进一步作为 GNNs 中消息聚合的控制器
这两个框架仍然可以利用稀疏结构来保持处理大型图的可扩展性。
理论上,作者证明了这两个框架可以区分传统 GNN 经常失效的几乎所有规则图中嵌入的节点集。还严格分析了它们的局限性。
实验上,作者在6个真实网络上分别从节点结构角色预测、链路预测和三角形预测三个方面对这两个框架进行了实证评估。
结果表明,DE-assisted GNNs 的平均准确率比没有 DEs 的 GNNs 提高了15%,DE-assisted GNNs 的性能也明显优于专门为这些相应任务设计的其他最先进的基线。
介绍

这项工作解决了 WLGNNs 的局限性,并提出了一类结构特征,称为距离编码(DE)。DE 既有理论保障,又有实证效率。
给定要学习其结构表示的节点集,图上节点的 DE 被定义为从感兴趣的节点集中的每个节点到该节点的随机游走的一组落地概率的映射。
DE 通常包括诸如最短路径距离(SPD)和广义 PageRank 分数之类的度量,其实质上捕获了图的结构信息。DE 可以通过简单而有效的方式融入到 GNN 的设计中:
-
首先,此文提出了 DEGNN,它利用 DE 作为额外的节点特征。 -
此外,通过允许 DE 控制 WLGNN 的聚合过程来进一步增强 DEGNN,这产生了另一个模型 DEAGNN。
由于 DE 完全依赖于图的结构,独立于节点标识符,因此具有归纳和泛化能力。此文的贡献如下:
-
从理论上分析了 DEGNN 和 DEAGNN 相对于 WLGNN 在结构表征学习中的附加表达能力。在表达能力方面,这两个模型能够区分嵌入在几乎所有稀疏规则图中的两个非同构的大小相等的节点集(包括节点、节点对、…、整体图),其中如果没有可用的区分节点/边属性,则 WLGNN 总是失效。 -
此文还证明了 这两个模型在学习距离正则图上节点的结构表示时并不比没有节点/边判别属性的 WLGNN 强,这意味着 DEs 的局限性。然而,作者还证明了它们在学习距离正则图上的节点对的结构表示方面具有额外的能力。 -
实证评估了这两个模型在节点角色分类(节点级)、链接预测(节点对级)、三角形预测(节点三联体级)三个任务层次上的性能。 提出的方法在所有三个任务上的预测平均准确率都比WLGNN显著提高了15%,也优于其他专门为这些任务设计的基线。
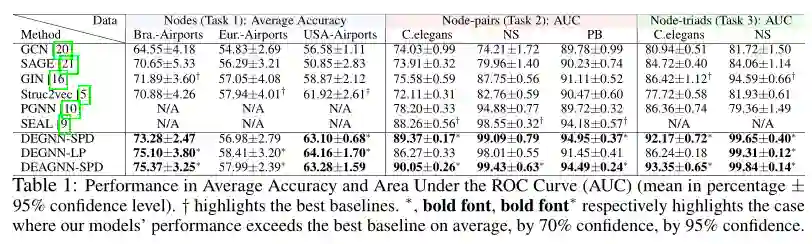
实验结果