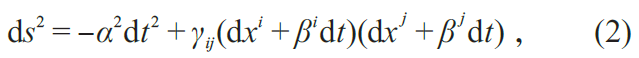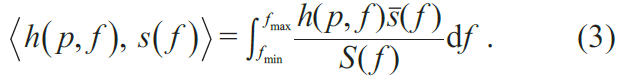数值相对论与双中子星并合

2019 年 10 月 17 日 中国物理学会期刊网

作者：周恩平 (德国马克思普朗克引力物理研究所)

摘要双中子星并合过程的引力波信号GW170817已经成功被LIGO直接探测，并合过程中的电磁对应体：短伽马射线暴GRB170817A以及光学、红外、紫外波段的千新星AT2017gfo也被多个天文台一同探测到，这标志着多信使天文学时代的开始。而数值相对论，即用数值模拟的方法研究双星并合的过程，在引力波探测、理解引力波源性质等方面起到举足轻重的作用。除此之外，数值相对论模拟的结果，也是我们理解千新星观测现象的重要工具。文章将回顾数值相对论建立、发展的历史，并介绍其在引力波探测、理解观测现象中所扮演的重要角色。

关键词 数值相对论，引力波天体物理，致密星物态

1 引言

引力，是四种基本相互作用中，人类最先接触并研究的力。300 多年前，牛顿在《自然哲学的数学原理》一书中，提出了平方反比的万有引力定律。200 多年之后的1915 年，爱因斯坦提出了基于相对性原理的利用几何语言来描述引力的广义相对论。在广义相对论中，引力被刻画为反映时空弯曲的一种几何属性(曲率张量)，而时空的曲率由处于其中的物质的能量、动量来决定，这就是著名的爱因斯坦场方程：

而在弯曲的时空中，不受任何外力的物体将沿着测地线运动，这就是所谓的物质决定时空如何弯曲，时空决定物质如何运动。牛顿的平方反比的万有引力定律，只是广义相对论在弱引力场下的一个极限。

爱因斯坦场方程，表面上看起来形式极其简单优美，实际上则不然，方程左边的爱因斯坦张量实际上包含时空度规张量的二阶导数，而方程右边的能动量张量也需要由度规张量才能确定，故而该方程实际上是一个非线性的二阶微分方程组。即使是写出这个方程的爱因斯坦本人，最初也只能通过近似的方法得到一些结果，比如水星近日点进动的计算、引力场中光线偏折角度的计算等等，以检验该理论的正确性。

为了寻求爱因斯坦场方程的精确解，人们首先研究了对称性最高、最简单的情形，即真空(从而方程右边为零) 球对称的静态解，该解由Schwarzschild 在一年后的1916 年得到。同年，Reissner 和Nordström得出了在有电荷情形下场方程的真空球对称静态解，即Reissner—Nordström解。这两个解分别对应了无电荷、无转动黑洞和有电荷无转动黑洞的时空。在起初的“势如破竹”之后，寻找场方程精确解就陷入了僵局，甚至只是放宽一点点对称性条件，就极大增加了求解的难度。一直到1963 年，Kerr 才给出了稳态轴对称条件下场方程的精确解，而一直过了10 年之后，1973 年，Schiffer 等人才给出Kerr 解的推导过程。在Kerr 解的基础上，Newman 发现了有电荷轴对称稳态时空的度规，即Kerr—Newman解。这两个解分别对应了无电荷转动黑洞和有电荷转动黑洞的时空。非真空的情形下，比如致密星体的内部，场方程大多数时候不存在精确解，比如最简单的球对称情形下，星体内部的度规和星体的结构可以通过结合物态方程与TOV 方程(由Tolman、Oppenheimer 和Volkoff 在1939 年推导而得)通过数值求解的方法来确定。

近百年里，人类所能得到的爱因斯坦场方程的精确解寥寥无几，而且上述所列出的解，大多也都是静态或者稳态时空的解，即其所刻画的时空不随时间变化。在研究双中子星、双黑洞并合这类广义相对论框架下的动力学问题时，这些稳态精确解所能提供的帮助非常有限。在20 世纪中叶，随着计算机计算性能的提升，许多复杂的物理、数学研究都借助于计算机模拟取得了突破，利用计算机通过数值模拟的方法求解爱因斯坦场方程来研究致密星、双致密星系统有关的物理问题，即数值相对论，这一研究方向也就应运而生了。

2 数值相对论的发展概况

相对论是人类时空观的一次飞跃，摒弃了伽利略和牛顿建立的时间和空间彼此独立毫无关联的绝对时空观。时空观的进步，却给数值计算带来了不便。在数值计算中，我们往往要把需要考虑的物理问题转化成一个初值问题，即把偏微分方程组改写为显含各个物理量对时间偏导的方程组的形式，这样在给定这些物理量的某个时刻的初始取值的情况下，就可以通过数值积分的方法在时间方向上演化这些物理量。

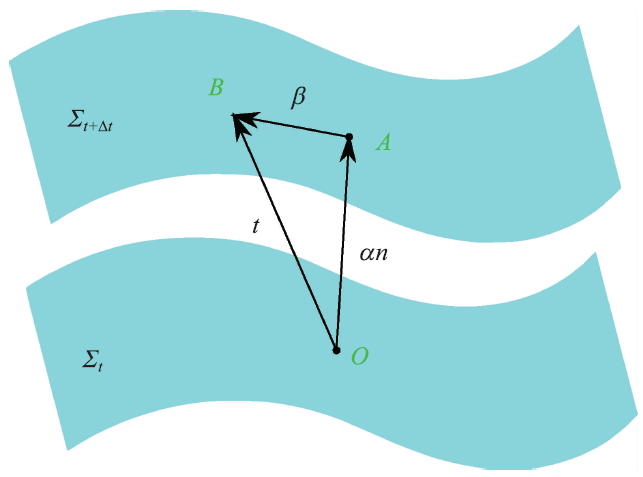
而如同上文提到的，在相对论的时空观里，并不存在绝对的时间和空间，爱因斯坦场方程定义在四维时空的背景上，而时空背景本身的性质则需要通过求解方程本身得到，由于方程是张量方程，具有协变性，一个时间坐标和三个空间坐标可以自由选取，通过不同的坐标选取方式，可以将张量形式的爱因斯坦场方程解构为不同的偏微分方程组。因此，要进行数值求解爱因斯坦场方程，首先要选择合适的时间坐标方向，从而把原本四维的时空，切割成一系列具有相同时间坐标的类空超平面，原本张量形式的爱因斯坦场方程也可以通过投影的方式被分解为若干显含时间偏导数的微分方程，这一步骤被称为3+1 分解(图1)，通过该分解，我们就可以把数值求解爱因斯坦场方程的过程变为两个步骤：首先确定对应某个初始时刻的超平面上的物理量(即初值问题)，再数值求解显含这些物理量对时间偏导的方程，从而求解后续时刻这些物理量的演化(演化问题)。

图1 3+1 分解的基本思路示意图^[2]，四维时空被切割成一系列具有相同时间坐标的类空超平面Σ_t ，原本四维时空度规g_μν的10 个分量被分解为γ_ij, α和βⁱ ，其中γ_ij为三维超平面Σ_t上的度规，有6 个自由度，而α和βⁱ被用以演化时间坐标和空间坐标，从而可以从一个超平面Σ_t把坐标系联系到下一个瞬时的超平面Σ_t_{+ Δt} 。特别地， α (lapse function)用以刻画超平面上某个点沿着法线方向到下一张超平面的固有时，而βi (shift vector)用以刻画沿着时间坐标方向移动到相邻超平面之后，与沿着法线方向所导致的偏离

1959 年，Arnowitt、Deser 和Misner 三人，针对爱因斯坦场方程进行了一种基于哈密顿量分析的3+1 分解形式，即ADM方程形式^[1]。在该形式下，四维时空的度规被写成如下形式：

其中γ_ij 代表分解得到的三维类空超平面上的度规，共有6 个自由度。由于对称性，爱因斯坦场方程共有10 个分量，而由于{t，x，y，z}4 个坐标可以自由选取，爱因斯坦场方程实际上只有6 个独立的分量。ADM分解显示了这一特性，分解而得的10 个方程里，只有6 个包含时间二阶导数，这6 个方程被称为演化方程。而另外4 个不包含时间二阶导数的方程则被称为约束方程。α和βⁱ 的4 个自由度，与后续演化过程中{t，x，y，z}4 个坐标的选取方式有关，也称为规范自由度，人们往往可以通过一些特定方法来选取α 和βⁱ ，以使得后续演化过程中的坐标系统依然能保证模拟的进行。

ADM方程形式被提出后，看起来，似乎只要我们先使用4 个约束方程在初始的一张超平面上求解出符合约束方程的初值，再利用6 个演化方程自由地演化这些得到的初值即可。然而，ADM 方程形式并不适合数值计算，这是由于ADM方程形式只有弱双曲性，因而在模拟过程中，由于计算机数值计算带来的小误差可能会持续积累并最终使得得到的解违背4 个约束条件，即长期演化得到的结果并不物理，数值计算不稳定。针对这一问题，Nakamura 在1987 年对标准的3+1 分解进行了改进^[3]，1995 年，Shibata 和Nakamura 进一步在共形变换的基础上进行改进^[4]，随后，Baumgarte 和Shapiro 在1999 年，引入了三维超平面的联络作为重要变量^[5]，该思路与Nakamura和Shibata 在1995 年的改进基本一致，不过得到的方程形式相对简单一些，这一改进了的3+1分解形式被称为BSSN方程形式¹⁾。

BSSN 方程形式改善了数值相对论的计算稳定性，而如前文所提到的，在演化过程中，还需要指定在演化后续时间里的坐标，即演化{t，x，y，z}坐标本身，通常，人们选择构建关于α 和βⁱ随时间演化的条件(即规范条件)，以达到此目的，然而，如何构造良好的、便于求解的并能保证演化稳定性的规范条件，也是一个棘手的问题，一个不好的规范条件选取，可能会导致随着时间演化，我们真正关心的致密星附近的空间分辨率越差，又或者不能有效避开时空中的奇点导致结果非数。这也是在BSSN 方程形式被提出的几年内，双致密星并合的演化并没有实质性进展的原因之一。

2000 年，Shibata 和Uryu 利用BSSN方程形式得到了首个成功的双中子星并合的三维数值相对论模拟工作^[6]，为了得到合适的坐标演化，该工作选择了求解抛物形式和椭圆形式的微分方程的方法确定α 和βⁱ，而非通过α 和βⁱ 对时间的偏导来直接演化它们。求解这种类型的方程时，需要在每一个时间步骤上反复迭代等待结果收敛，非常耗时。而另一方面，双中子星系统与双黑洞系统不同，大部分时间里不涉及时空奇点的出现。该工作中使用到的方法并不能简单地直接照搬到双黑洞系统里。

2003 年，Alcubierre 等人提出了一种后被称为移动穿刺规范的规范条件^[7]，该条件可以有效避免坐标接近时空中的奇异点，对于黑洞的模拟很有帮助，并且规范条件用双曲方程形式来刻画，数值计算效率很高。利用这一规范条件，他们得到了成功的单个黑洞的数值相对论演化结果。

当大多数研究都把注意力放在BSSN 方程形式下的数值相对论演化时，2005 年，Pretorius 等人出乎意料地先拔头筹，用广义调和坐标计算方程形式(GH方程形式)成功得到了双黑洞并合的演化^[8，9]。而延续Alcubierre 等人的移动穿刺法的工作在随后才取得进展，在2006 年，Baker 等人和Campanelli 等人分别独立地得到了成功的双黑洞并合的数值相对论演化结果^[10，11]。与Alcubierre 的工作相比，他们均采用了四阶有效差分的方法来代替原本的二阶精度，更加保证了程序的精确性和稳定性，并且通过变量替换的方式对原BSSN方程形式进行了改写，解决了一些变量在某些坐标位置上发散的性质，使之更好地与移动穿刺规范搭配。这些工作宣告了3+1 分解形式下，数值相对论演化的稳定性问题得到了解决。

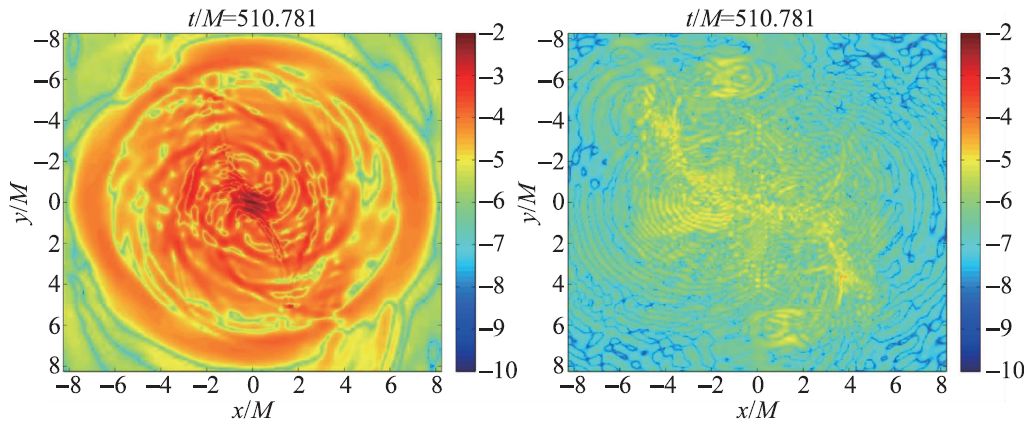
稳定性得到解决之后，就需要关注数值相对论结果的精确程度问题。数值相对论结果的精度往往由所谓的约束违反程度来刻画。如前文所介绍，爱因斯坦场方程可以被分解得到4 个不含时间二阶偏导的约束方程，在进行数值相对论演化时，往往不需要求解这4个方程，只要给定的初值满足约束方程，那么利用其他几个演化方程演化所得到的后续结果应当自动满足这4 个约束方程，这种演化方式也被称为自由演化。然而由于数值计算过程中精度有限，随着演化的进行，所得到的结果往往不再满足约束方程而是会有一定偏离，通过分析BSSN 方程形式可以发现，在该方程形式中，哈密顿约束违反的传播速度是0。换言之，在计算过程中产生的约束违反会一直累积，比如在双中子星并合的模拟中，双中子星并合瞬间，以及中子星坍缩成黑洞瞬间，往往会导致约束违反激增，而在BSSN 方程形式下，这些在特定时间点产生的约束违反会一直停留在计算区域内累积，导致后续的结果精度也下降。针对这一问题，一种可以有效衰减约束违反的Z4 方程形式被提出，而其两个共形版本：CCZ4 和Z4c 方程形式都被用于数值相对论演化，相比于BSSN 方程形式，精度提高了2到3个数量级^[12，13](图2)。

图2 BSSN方程形式(左侧)与Z4c方程形式(右侧)进行双中子星并合模拟过程中的约束违反情况^[13]。图中选取的时刻接近并合发生的时刻，可以看出使用Z4c方程形式，精确程度提高了两个数量级

相比于双黑洞并合过程，双中子星的并合牵扯到更多更复杂的物理过程。比如流体的粘滞性、有限温度效应，往往会直接影响抛射物质质量的多少和速度的大小，并合之后产生的大质量中子星温度很高，是非常有效的中微子辐射源，这些中微子辐射又会影响抛射物的中子丰度，而抛射物质的质量、速度和中子丰度，又决定了双中子星并合过程中电磁对应体的特征。此外，中子星往往具有强磁场，而该磁场又会在并合过程中被进一步强化，而这一强磁场也是双中子星并合过程中产生相对论性喷流并导致伽马射线暴的关键因素。因而，为了理解观测现象、从观测中理解天体物理过程，在数值相对论模拟中，加入粘滞性、中微子辐射、有限温度物态模型和磁流体力学模型也是非常重要的，这也是近年来用数值相对论研究双中子星并合的前沿方向。

3 数值相对论与双中子星并合

3.1 引力波探测与数据分析

引力波探测过程中，往往需要面临要探测的引力波信号比探测器噪声要低几个数量级的情况，为了从噪声海洋中挖掘出想要探测的引力波信号，往往需要用到一种被称为匹配滤波的方法：

在该表达式中，f 表示的是信号对应的频率，而s(f )就是频域内的实验数据，S(f )是探测器的噪声功率谱，通过这样的处理，就可以比对观测信号与理论预期信号的一致性，如果我们遍历所有的模板参数p，使得上式的结果超过某个阈值，就可以断定引力波信号被探测到，而引力波波源的性质最可能是由p刻画。

由此可见，引力波探测能否成功，取决于是否知道“想要观测到什么”，即一个精确的引力波源理论模型库h(p, f )，是帮助我们挖掘出埋藏在噪声中的有效信息的关键。

在实际的引力波探测中，数值相对论并不适合直接被用来构建引力波模板库，这一方面是由于三维的数值相对论模拟的时间消耗远远超出其他近似模型(比如后牛顿近似)，而实际的引力波探测则需要我们的模板库尽可能覆盖更多的引力波源参数p，数值相对论的时间代价显得有些难以承受。另一方面，在匹配滤波的表达式中，被用来积分的理论模板模型和观测数据，只在某个频率范围内，而目前引力波探测器的最灵敏的频段主要集中在几十到几百赫兹左右，与之相比，数值相对论的模拟往往是从双星并合前的几个轨道开始进行，对于恒星质量级的双黑洞系统或者双中子星系统来说，数值相对论模拟的结果也难以覆盖探测器最灵敏的频段。

当然，这并不是说数值相对论的工作对于引力波探测本身没有意义。通过近似方法得到引力波模板库固然快速高效，却并不能保证近似模型在强场下的准确性和收敛性，这时就需要利用一些数值相对论的结果来对近似模型进行验证和定标。在LIGO 实际探测中被广泛使用的有效单体数值相对论模型(EOBNR模型)^[14]，就是这样一种使用有效模型近似并和少量数值相对论结果对比定标而建立起来的模型，从而兼顾了计算效率和准确性，适合实际观测中使用。

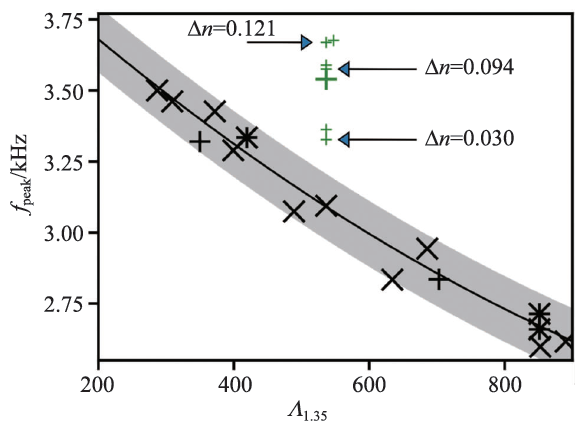
除此之外，包括EOBNR 模型在内的有效模型，往往把并合的致密星抽象成质量、自旋、潮汐形变能力等少数几个整体参数，而忽略星体具体的内部结构，因而只能得到星体旋进阶段的引力波模板，而双中子星并合之后，往往会形成一个短暂存在的快速转动的高温大质量中子星，该中子星的非轴对称形变、星体本身的震荡等等，都会产生信息非常丰富的引力波信号，如果我们想要研究这些并合后的引力波信号，就不得不借助数值相对论了。通过数值相对论的方法对大量不同物态的双中子星系统进行模拟之后，人们发现并合后期的引力波信号中，最显著的峰值频率与双星的约化潮汐形变能力有着明显的关联，而且此关联并不依赖于具体的物态模型，这无疑对于我们利用未来的引力波信号来限定中子星物态提供了很有用的线索(图3)。

图3 数值相对论的模拟结果暗示了可能通过并合后引力波信号的峰值频率来理解并合过程中致密物质是否发生了强相互作用相变^[15]。图中黑色的记号代表的是使用纯粹强子物质模型的物态，其并合后引力波信号的主导频率与星体潮汐形变能力的关联，绿色的符号为考虑了强相互作用相变可能性的物态得出的结果。可以看出，由于强相互作用相变会使得物态变软，星体收缩，因而震荡频率会变大而偏离强子物质物态预言的结果。该图中显示的模型都是1.35—1.35 太阳质量的双中子星并合模型

而近期的一些工作在考虑了强相互作用相变的可能性之后，发现了一种有趣的可能性，在并合之前，两个互相绕转的中子星质量较小密度较低，是经典的中子星物态模型描述，而在并合发生后，因为质量大大增加，星体的中心密度也会随之变大，星体中心区域可能会出现一个导致强相互作用相变发生的高密度区域，夸克物质可能出现在这个区域里，相变发生后，因为物质变到了更稳定也就是能量更低的状态，因而中子星变“软”了，在引力的作用下，变软了的中子星半径会有一定收缩，根据上文的描述，星体震荡的频率会因此变大并偏离原本的不依赖于物态与潮汐形变能力的关联^[15]。这种信号，可能在未来的观测中帮助我们更好地了解强相互作用物质的物态，而这些可能性，都得益于数值相对论的模拟。

3.2 抛射物性质

双中子星并合与双黑洞并合的一个最大不同，在于双黑洞并合只是纯粹的时空动力学，并没有“物质”形式的存在，而双中子星并合则由爱因斯坦场方程与流体力学方程一同刻画，在并合过程中，会有丰富的物质抛射现象，这些抛射物会带来的丰富电磁波段的辐射，比如随着GW170817 事件一同被探测到的伽马射线暴GRB170817A和千新星AT2017gfo^[16-18]，都成为我们了解并合双中子星性质的关键。

早期的数值相对论模拟，往往使用简单的多方物态方程描述中子星，能动量张量也使用理想流体的形式来描述，因而无法顾及实际物理中的流体粘滞性。近年来，有限温度的物态模型被广泛应用于双中子星并合的模拟中，更加具体细致的物理图像，比如中微子辐射转移、流体粘滞性等等也被加入，使得我们可以通过数值相对论模拟更准确地把握抛射物的性质。

通过模拟发现，双中子星并合过程中产生的抛射物主要分为两类，一类被称为动力学抛射物，另一类被称为盘风抛射物。前者主要是由并合本身的动力学过程导致，比如在双星旋进阶段，由于潮汐力矩就会导致大量的中子星物质在公转轨道面方向上被抛出，由于此时双星还未直接接触，温度很低，这些抛射物也以富中子物质为主；而在双星旋进并接触的瞬间，星体互相挤压导致接触面上会产生激波，并在两极的方向上抛射出大量物质，此时由于双中子星已经直接接触，温度大幅升高，大量的中微子辐射会改变抛射物的成分，使得中子的比例下降。盘风抛射物形成于星体并合之后，双中子星并合之后，星体外会有一定质量的仍然被引力束缚的物质形成遗迹盘，由于盘内的粘滞性导致的角动量转移，以及来自并合之后形成的高温中子星的中微子辐射和星风驱动，会导致物质从盘内被抛出，同样由于高温和中微子照射，这一部分抛射物的中子丰度也相对较低^[19]。

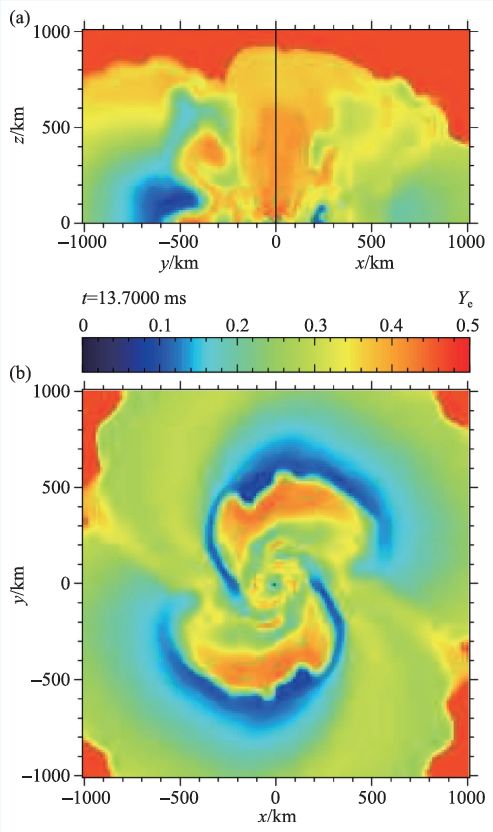
抛射物内的中子丰度会决定后续的核合成的元素种类，从而导致不同机制产生的抛射物会具有不同的光学不透明度，这些都会影响千新星的观测性质，故而可以通过具体的观测现象来推断抛射物的性质。而通过数值相对论来模拟各种不同物态、不同质量的双中子星并合过程，也可以帮我们理解这些不同成分抛射物的多寡与中子星物态和双星参数之间的关系(图4)。从而，依靠数值相对论作为纽带，我们可以通过千新星的观测来直接限制中子星的物态。

图4 数值相对论模拟显示的双中子星并合过程中产生的抛射物以及其中子丰度^[19]。图中颜色代表的是电子与重子的数目比Y_e，蓝色区域代表低Ye 即丰中子，红色区域代表Y_e~0.5 ，即中子与质子数目相当。图中分别是从公转赤道平面侧视(a)与从公转轴上方俯视(b)的视角。从图中可以看出，在旋进过程中产生的丰中子抛射物由于产生较早，比较靠外侧并分布在赤道面上(蓝色区域)，而并合后由盘风和粘滞性驱动的长期的抛射物，中子丰度已经大大降低

数值相对论的结果显示，潮汐力矩导致的物质抛射，与中子星本身的潮汐形变能力有关联，如同其名字一样，潮汐形变能力较大的物态，这一部分抛射物会相应较多。激波导致的动力学抛射物，与物态之间没有明显关联，除非物态特别软，在并合之后迅速形成了黑洞，在这种情况下，该部分抛射物的量会明显降低。盘风抛射物主要依靠遗迹盘的粘滞性和中心天体的中微子辐射来驱动，因而其总量的多少取决于并合形成的大质量中子星在坍缩为黑洞之前能存在多久。

AT2017gfo 的观测特点显示了明显的红、蓝两个成分，根据观测现象推断，应该有相当比例的抛射物并非富中子的^[20]，这暗示了在并合之后，形成的大质量中子星在坍缩为黑洞之前可能存在了较久的时间( 秒的量级)。无独有偶，GRB170817A的观测同样也暗示了这一点^[21]，根据包含磁流体力学的数值相对论模拟结果，并合产生的大质量中子星往往具有很强的较差自转，这种较差自转会显著放大星体的磁场，这种强磁场被认为是产生伽马射线暴所必须的相对论性集束物质喷流的关键。综合这些观测现象，并结合大量数值相对论的模拟结果，中子星的极限质量( MTOV )被限定在2.1—3.35 太阳质量之间^[22]，这也成为了了解中子星物态和内部结构的重要线索。

3.3 无延迟坍缩临界质量

双中子星并合并非总会产生一个大质量中子星之后才延迟坍缩为黑洞，如果双中子星的总质量太大，远远超过中子星的极限质量，那么并合之后不经过任何延迟就会直接坍缩为黑洞，通过上文的分析，这种情况显然并没有发生在GW170817 这一双中子星并合事件中，而这一事件中双星总质量得以被精确测量，这也就意味着如果我们能找到双中子星并合时间中发生无延迟坍缩的临界双星总质量与物态的关系，便可用GW170817 的观测事实来对中子星物态进行限制，而数值相对论的模拟就可以帮我们研究这个临界质量。

由于并合时星体的热压也可以帮助抵抗坍缩，所以想要研究这一临界质量，必须使用温度依赖的物态模型。在实际研究中，我们可以选定某种物态并逐步增加模拟星体的总质量，通过其在模拟中是否发生了无延迟坍缩，来确定这个临界质量的大小。通常来说，因为不同的中子星物态本来就有不同的不转动极限质量M_TOV，所以我们往往更关心这个无延迟坍缩的临界质量与M_TOV的比值k =M_threshold /M_TOV 。

模拟的结果表明，这个比值k 因物态的不同而有不同的取值，但是与不同的物态的不转动极限质量解对应的致密度C_TOV =M_TOV /R_TOV具有负相关性。这一负相关性可以定性来理解，黑洞的致密度固定为0.5，而中子星的致密度都小于这个值。这也就是说C_TOV 越大的中子星，本身就半径更小，更接近于黑洞的致密度，因而并合之后的大质量中子星也更容易坍缩为黑洞，即k 值越小。数值相对论的模拟结果定量得显示k 与C_TOV有着简单的线性关系。而对于GW170817 来说，由于并没有发生无延迟坍缩，故有双星总质量小于临界质量，这一事实便可被用来限制中子星的半径R_TOV ≥9.26 km^[23]。

未来，通过更多的双中子星并合事件的观测，我们会获取更丰富的关于临界质量的信息。比如，如果我们测到了比GW170817 更大质量的并合事件，并且有观测表明没有发生无延迟坍缩，那么就可以利用同样的分析方法进一步提升R_TOV 的下限，对物态模型进行更严格的限制；反之，如果未来探测到了无延迟坍缩并合事件的发生，那么我们就将同时得到关于R_TOV的下限和上限的信息，从而把半径限制在一个非常小的范围内，于此同时， M_TOV 的上限也将被限定出来，这对于限制中子星物态模型可能会起到一锤定音的效果。

4 总结与展望

从1905 年的狭义相对论到1915 年的广义相对论，爱因斯坦花费了10 年的时间把时间和空间联系在一起并用四维时空的几何性质来理解引力，而为了能够更广泛地应用这一理论，我们已经花费了半个多世纪的时间想要把纠缠在一起的时间和空间拆解开来，数值求解。虽然路程并不一帆风顺，但也已经取得诸多成果：以数值相对论为定标基准的引力波模板，帮助我们从噪声中挖掘出了包括GW170817 在内的许多双星并合信号并分析了引力波源的参数；数值相对论模拟的结果也帮助我们更好地理解了千新星AT2017gfo 和短伽马射线暴GRB170817A 的观测现象；通过观测并结合数值相对论的结果，我们获得了更多关于致密物质物态和中子星内部结构的线索^[24]。当然，我们也必须看到，受到计算能力和计算资源的限制，数值相对论还远远不是一个能完整刻画双中子星并合过程中所有物理过程的模型，中微子、粘滞性的刻画，目前都只是一些近似模型，受限于有限的空间分辨率，许多小尺度的物理过程细节也没有办法得以体现，而受到模拟时间的限制，现在的数值相对论模拟，往往只能覆盖大概数百毫秒的真实物理时间，这使得我们很难完全把握从旋进到黑洞形成的整个过程。相信数值相对论学家们也不会满足于暂时的成功，一定会继续完善改进，让数值相对论能够成为贯穿多信使天文学的重要工具。

1) BSSN分别是为这一方程形式做出贡献的Baumgarte，Shapiro，Shibata 和Nakamura 四人姓氏的首字母。实际上Shibata和Nakamura对此领域的贡献要比Baumgarte 和Shapiro 早了几年。只是由于历史原因，日本的数值相对论学术圈在当时并不具有很强的国际影响力，在1999 年Baumgarte 和Shapiro 的工作发表之前，Shibata 和Nakamura 的工作几乎不为西方学术圈所知，因而最终命名时是按照BSSN的次序。

参考文献

[1] Arnowitt R，Deser S，Misner C. Physical Review，1959，116：1322

[2] Shibata M. Numerical Relativity.World Scientific，2016

[3] Nakamura T，Oohara K，Kojima Y. Prog. Theor. Phys. Suppl.，1987，90：1

[4] Shibata M，Nakamura T. Phys. Rev. D，1995，52：5428

[5] Baumgarte TW，Shapiro S L. Phys. Rev. D，1999，59：024007

[6] Shibata M，Uryu K. Phys. Rev. D，2000，74：121503

[7] Alcubierre M，Brügmann B，Diener P et al. Phys. Rev. D，2003，67：084023

[8] Pretorius F. Phys. Rev. Lett.，2005，95：121101

[9] Pretorius F. Class. Quantum Grav.，2005，22：425

[10] Baker J G，Centrella J，Choi D I et al. Phys. Rev. Lett.，2006，96：111102

[11] Campanelli M，Lousto C O，Marronetti P et al. Phys. Rev. Lett.，2006，96：111101