灭霸力气有多大？钢铁侠战衣有多重？科学家是这样看漫威的

2018 年 5 月 30 日 中科院物理所

你对漫威中的科学了解多少？打住，这里问的并不是什么非洲科技大国瓦坎达，而是从漫画中发现的科学问题，例如能轻松捏碎宇宙魔方的灭霸，力气能有多大？

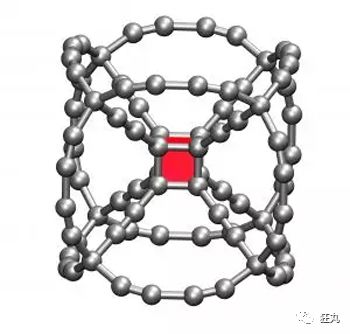
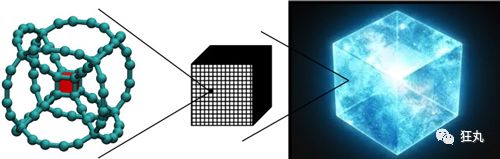
马萨诸塞州理工学院土木工程博士Steven W. Cranford通过模拟宇宙魔方的强度，估算了灭霸的力量，并将结果发表到了Nature物理博客上。首先他认为宇宙魔方并不是普通的立方体，而是一种超立方体，也就是立方体的四维类似物。

（立方体中包含立方体）

基于这个概念，Cranford通过建模软件开始尝试构建宇宙魔方，并使用了一种，目前仅理论上存在的世界最强材料「碳炔」作为构建魔方的素材，据说它的强度是钻石的40倍。通过调整组合，他构建出了一个边缘稍微弯曲的超立方体，并称其「超立方炔」。

虽然单个超立方炔在模拟测试中表现出的强度并不高，但把数十亿个它，像乐高积木一样连接在一起，它的强度就会飙升到科幻片的层次。以边长为6英寸的宇宙魔方为例，Cranford计算出想要捏碎由立方炔组成的它需要42000吨的力量，而普通人的握力才50公斤，这个概念相当于灭霸的握力比正常人大750000倍，进步一估算，灭霸最少可以举起50000吨的重量。

我们再「夸张」的假设一下，钢铁侠的某套装甲可以提升其握力1000倍，那么钢铁侠的握力则是50吨，需要840套这样的战衣才能抗住灭霸的随手一握。所以你不得不承认，能接住灭霸一拳的美队，真的很史蒂夫·五五开。

像Cranford这种科学家狂丸一般喜欢称他们为「科技杠」。他们学识渊博，但尊重漫画原作，而且特别喜欢用自己的所学将科技与艺术进行融合，总结出让你瞠目结舌的理论。这其中的佼佼者，还有一位名叫James Kakalios的物理学家。

James目前是尼苏达大学物理学教授，去年又被授予了英国林肯大学荣誉科学博士学位，专攻非晶半导体，喜欢用科学解读美漫。他刷新了狂丸对超级英雄的认识，从他的《魔鬼物理学》中，狂丸学会了一种粗略计算钢铁侠战衣实际重量的方式。

（影视作品中的Mark2）

以1963年时出版的战衣为例。首先要估算出钢铁侠战衣的表面积，James的计算思维很简单，把钢铁侠本人看成一个圆柱体，而他的四肢和头看做四个小圆柱体。那么身高6英尺，衣服为50码的史塔克，战衣的总表面积就是26200平方厘米。

然后目测钢铁侠的战衣厚度为8分之一英寸，也就是0.3175厘米，而盔甲的面积需要乘一下厚度，就能得出一个大致的体积：8400立方厘米。剩下来只要知道材质与其密度，重量就能估算的八九不离十，例如铁材料的战衣重：67千克，钛合金材料会轻一些，大约：37千克。

关于漫威设定中，最大的悬案之一还有：「蚁人的力气，在变小后是怎么保持和正常人类一样的」，James利用物理学也找到了答案。

他首先确定了一点：那就是蚁人的密度始终没变，这也就意味着质量一定是随着身体一起缩小的。例如在《惊异故事》第37期中，蚁人因为质量小而被吸入吸尘器，另外他还能乘骑老鼠。

但问题是，他是怎么拥有成年人的力量，并打破了吸尘袋逃出生天的。这就相当于个能一拳打翻成年人的超级英雄，却会有可能被一辆玩具车撞死，很不合理。

James从人力的来源开始分析。首先力量来源自肌肉与骨骼一起组成的杠杆结构，例如前臂、肘部、肱二头肌三人组。

所以从肌肉比例上就不难分析蚁人变小后到底拥有多大的力量。以普通人类为准，如果他的缩小到人体的1%，那么他的肌肉产生的力量就要缩减为原来的0.0001。那么正常人来说一拳能打出200磅的拳力，蚁人的一拳也就0.02磅。

但问题是，挥动拳头与扔东西不同，如果要观察伤害输出，那么还要考虑拳头的横截面带来的压强。

这样一计算就明朗了。蚁人的拳头要比正常人小很多，假设手部约为1毫米宽，那么横截面只有0.0005平方英寸，他出拳时产生的「单位面积受力」，是两者相除，即为每平方英寸40磅力，这显然能够帮助它脱困。

有趣的是，我们可以对比一下，结合前文所说，正常一拳的力量是200磅力，同时正常拳头的横截面是5平方英寸，那么结果每平方英寸所受的压力也是40磅。换言之，在这一拳上，虽然力量变小了，但蚂蚁大小的蚁人确实挥出了与正常人大小不相上下的效果。

而James最常讨论的超级英雄是蜘蛛侠，因为蛛丝的使用与物理学有着紧密关联。例如他在楼宇间荡来荡去，蛛丝真的不会断么？

James Kakalios的切入点是两方面：蛛丝的承重，与蛛丝能够承受多少力。通过蜘蛛侠的一贯走位风格不难看出，蛛丝在蜘蛛侠的走位过程中受到了两种力，自身体体重产生的拉力，与漂移改变自身方向产生的向心力。

于是假设蜘蛛侠常用的蛛丝长度为200英尺，摆荡耳朵速度50英里/小时，体重大约是73千克，根据向心力加速度公式a=v²/R ，James计算出拉住身体需要160磅力，而为了让直线运动轨迹变成圆周运动轨迹，蛛丝还需要额外提供135磅力的力，因此总计约为300磅的力。

所以蛛丝抗的住么？如果是纯粹的蛛丝，那绝对没有问题。正常的蛛丝能够承受每平方厘米20000磅力的压强，换句话说，蜘蛛侠喷出的蛛丝只要截面超过1厘米，就能承受10吨的重量，而以蜘蛛侠的出货量来看提起600磅都没问题。

甚至「由蛛丝编成的绳子只需要有铅笔那么粗，就可以阻止战斗机在航母上降落」。所以说蜘蛛丝缝合游轮、拦截高铁这些场面看着很科幻，其实也是遵循基本法的。

另外James最得意的推理是关于「漫威史上最大冤案之一」的计算，那就是蜘蛛侠竟然亲手杀死过自己的女友，然后反派竟然替主角背了近30年的黑锅。这段故事发生在《神奇蜘蛛侠》第121期，绿魔绑架了蜘蛛侠的女友格温·斯黛西，把她带到了乔治华盛顿大桥的顶端，然后一不小心推了下去。

关键时刻蜘蛛侠射了一滩蛛丝，接着「咔嚓」一声，帮助斯黛茜停止了坠落。

谁成想，温格还是死了。而对于如何死的，很多读者都有不同解读，漫画中绿魔强行背锅，对蜘蛛侠说「从那么高的地方摔下去，不管是谁都死定了，根本不用撞击到地面」。

在James看来显然不是这么回事，真正导致死亡的根本不是坠落，而是骤停。首先要了解一个关键问题：蜘蛛侠射出的蛛丝拉住温格时承受了多大的力？

（感觉过程有点像悠悠球）

要知道，这个力越大，温格在空中减速所花费的时间也就越少，也就是急停刹车越快。当然这个力越大越危险，就像安全气囊很柔软，但瞬间的弹射力依然能够把人击晕。根据这个关系，这个力其实包含在温格停顿瞬间产生的「冲量」里，也就是力对时间的积累效应，用公式表达为F*t=m*（v2－v1）。这里F就是我们所求的力，t是减速所花费的时间，m则是妹子的体重，v2－v1则代表速度的变化，也就是：

接下来直接计算就好。首先比较难确定的是「速度的变化量」，据漫画视角，温格被拉住的位置大概是距离桥顶300英尺左右的地方，根据重力与掉落距离计算下来坠落速度是95英里/小时。那么速度的变化量就是：95英里/小时-0英里/小时=95英里/小时。

接着假设妹子体重110磅，也就是50千克，蜘蛛丝让其静止的时间是0.5秒，所产生的力就是970磅，也就是用了温格体重10倍的力，才让她停止坠落。相当于什么概念呢？那就是蜘蛛侠射出蛛丝拉住温格的效果与让她直接pia唧一声摔到水面基本上没区别。换句话说，温格就像大多数落水者一样，在被蛛丝的力量拯救时，咔嚓一下「摔断了」脖子。