Thinking Above Code：TLA+ 思维概述

2021 年 12 月 9 日 InfoQ

作者｜李明昊

策划｜蔡芳芳

本文是《Thinking Above Code：TLA+ 从入门到实践》系列文章第一篇。

TLA+ 是 Paxos 算法发明者 Leslie Lamport 的大作。它是一套数学建模工具箱，用于给分布式系统建模。这个工具箱主要包括形式化建模语言 TLA+ 和形式化验证工具 TLC model checker。

如今 Paxos 算法几乎成了分布式系统一致性算法的事实标准。市面上流行的大多数分布式系统都直接使用了 Paxos 算法或其某个变种。但相信搞过分布式系统的朋友们都会对 Paxos 算法坎坷的问世过程有所了解。

曾经 Lamport 为了能生动形象的表述算法，假借考古学家的口吻讲述了古希腊 Paxos 岛上兼职议会（The Part-Time Parliament）的运作过程。论文投出去后，审稿者觉得这种口吻过于随意，不符合技术文章的风格，没有给出积极的回应。Lamport 自己甚至还假扮考古学家做了几次演讲，讲述 Paxos 算法，均收效甚微。大家觉得 Paxos 这个东西太复杂，没有人知道他到底在说什么。

之后 Lamport 自己又写了一篇文章《Paxos Made Simple》进一步介绍 Paxos，通篇几乎没有任何数学符号。可这时人们又觉得 Paxos 算法不够严谨，缺少严格的数学证明。

直到新世纪之后，互联网浪潮风起云涌，席卷全球。Google 作为互联网时代的领军者，声称在自家的分布式锁服务 Chubby 中引入了 Paxos 算法。此后，Paxos 算法一战成名，成为分布式系统一致性算法的事实标准。

2013 年，Lamport 也因为对分布式系统的重大贡献，成为当年的图灵奖得主。曾经有不少人质疑 Paxos 算法的数学严谨性。殊不知，Lamport 本人曾就读于麻省理工的数学专业，对于数学和物理学都有着极高的造诣。Paxos 算法也是他多年使用数学思维为分布式系统建模，进而设计出来的。

多年后，他又把自己的数学思维形式化成为一套具体的数学语言，也就是 TLA+。同时，也开发出了一套可用的形式化验证工具软件，也就是 TLC model checker。Lamport 曾经穿着一件印有“You Want Proof? I'll Give You Proof!”的 T 恤衫演讲，不知是否是对这些人的回击。看来这老爷子是个老顽童。^_^

1 TLA+ 简介

相信开发过分布式系统的朋友们都遇到过这种场景：系统开发完成后，通过了所有的测试用例，于是我们信心满满的将其上线了。可是线上系统跑着跑着，不知哪一天突然莫名其妙地出现了一些 bug。当我们打开日志，打开 GDB，准备追踪定位这些问题时，它们又无法复现了。可如果放任不管，不知什么时候，它们又会诡异地冒出来。这种 bug 非常棘手，甚至让开发者很崩溃。这个问题本质上是因为分布式系统过于复杂，测试 case 很难覆盖所有可能的运行场景所导致的。再怎么细心，总会存在某些 corner case。当系统运行到这些场景时，bug 就出现了。

怎么系统地解决这种问题呢？答案就是本文的主角——TLA+。

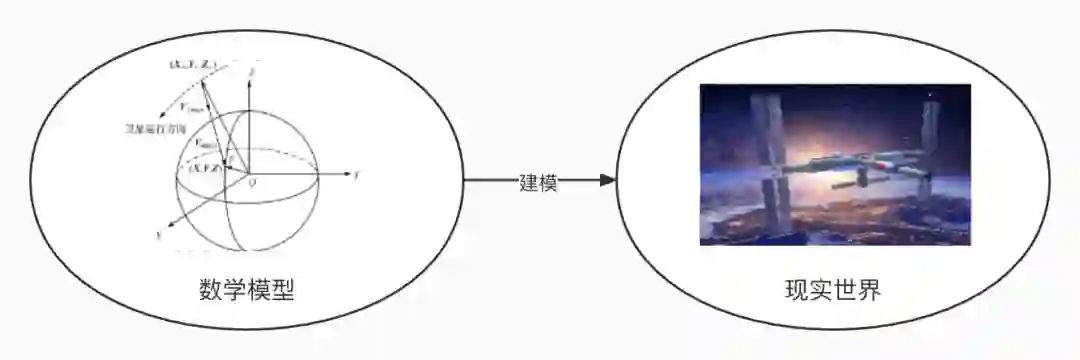
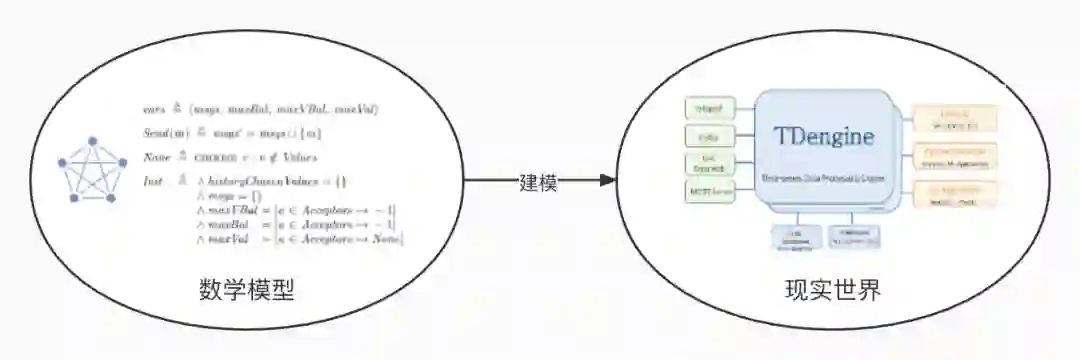
读者朋友应该对数学建模的过程非常熟悉：我们使用某种数学语言给现实世界中要研究的问题建立数学模型，然后从数学上推导论证模型的某些性质，进而预测在现实世界中未来的趋势。

TLA+ 就是为分布式系统建模的数学语言（主要用到了数理逻辑、集合论和图论三个数学工具）。我们使用 TLA+ 为我们的分布式算法建模，同时针对实际系统的运行场景给出若干约束条件，然后再使用 TLC model checker 去验证模型是否满足这些约束条件。如果验证通过，我们再用具体的编程语言（比如C/C++）把算法编程实现出来。这样系统开发完成后，即使再遇到某些 bug，也都是编程过程中本身的 bug，都比较好处理。分布式算法上不会再有问题。

TDengine 作为一款开源的分布式时序数据库软件，主要面对的是物联网这个复杂的运行环境。在物联网场景下，怎么保证数据的一致性，同时兼顾读写性能，是一个非常大的挑战。我们对 TLA+ 做了一些探索，用 TLA+ 为 TDengine 的分布式算法建模（基于物联网场景下改进的 Raft 算法），以保证其性能和正确性。后续我们会通过一系列文章，讲述探索和实践的过程，供大家参考。

2 状态机模型（state machine）

状态（state）

可以用状态（state）来描述某个系统在某一时刻的性质。状态是什么呢？就是一堆变量。比如用长宽高描述一个箱子，用速度与加速度描述一个运动中的物体。在计算机世界中，同样可以用一堆变量描述系统当下的状态。比如用 msgs、maxBal、maxVBal 和 maxVal 4 个变量描述一个 Paxos 节点，用 currentTerm、state 等 9 个状态描述一个 Raft 节点。

状态转变

在自然界中，物体的状态是可以随时间发生改变的，通常用时间 t 的函数 f(t) 来描述物体的当下状态。比如位移 = 速度 x 时间，s=f(t) = vt。这里的时间 t 是一个连续的变量。大部分的物理学定律都是这样，将某些物理量定义为时间 t 的函数。

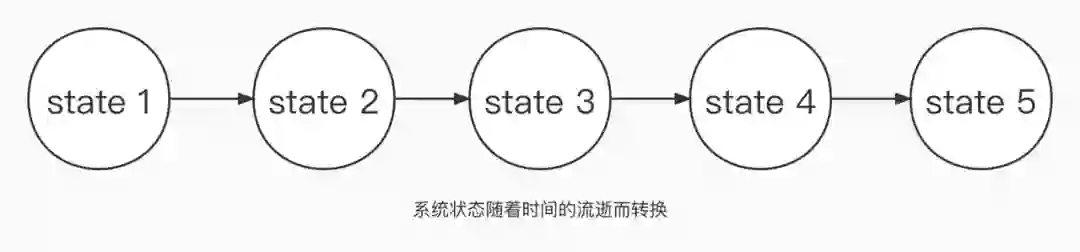
在计算机世界中，同样也可以把系统状态描述为时间 t 的函数，只是这里的时间是一个离散量，具体来说，就是 CPU 中的时钟滴答。系统随时间的改变，就可以看成一系列离散的状态变化。

3 分布式系统

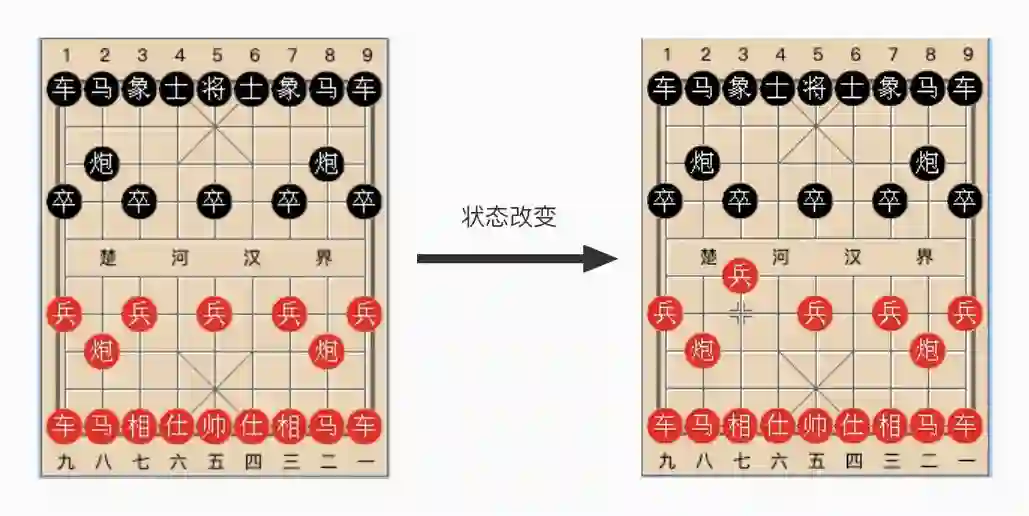
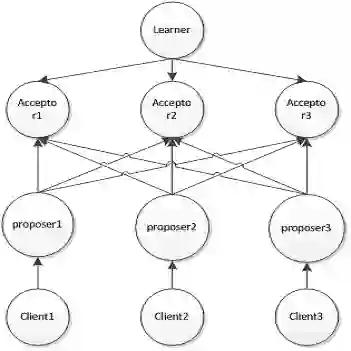
分布式系统包括多个节点，我们把所有节点状态的集合看成一个统一的全局状态，用这个统一的全局状态来描述一个分布式系统。下面是一个 Raft 系统的全局状态。

通过对比可以看到，原来 Raft 单节点变量变成了数组，包括 currentTerm、state、votedFor 和 commitIndex。而原来的数组变量变成了二维数组，包括 log、votesResponded、votesGranted、nextIndex 和 matchIndex。另外增加了一个 msg 变量，用来描述系统节点发出的网络消息。

看到这里，大家可能会有点晕。不过没关系，这里只是概要地介绍一下，让大家对 TLA+ 的思维方式先有个印象。后续这些变量究竟是什么意思、怎么使用，我们还会详细介绍。

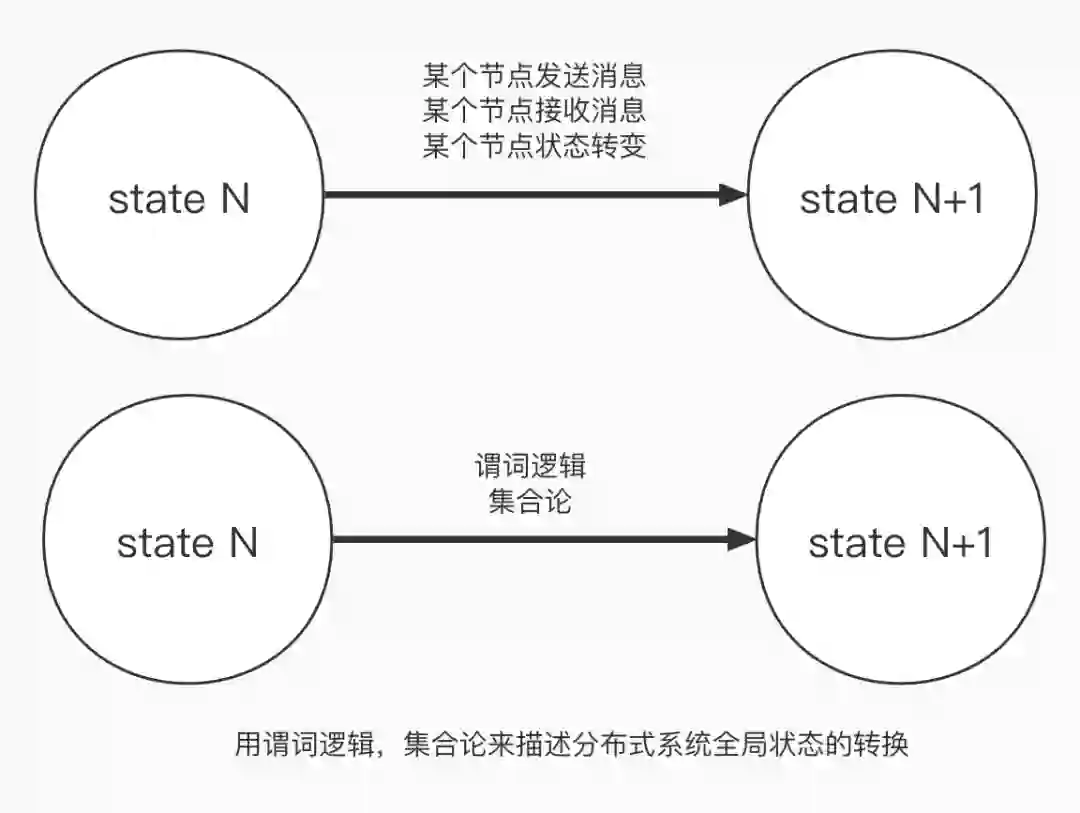
怎样定义全局状态的转换呢？直观上我们可以想到：如果某个节点自身的状态发生了改变，那么全局状态自然也会发生改变。另外，如果某个节点发送了一条网络消息，或者某个节点接收了一条网络消息，全局状态也会发生改变。所以，引起系统全局状态改变的原因包括分布式系统中任一节点自身的状态改变和系统中消息的发送。

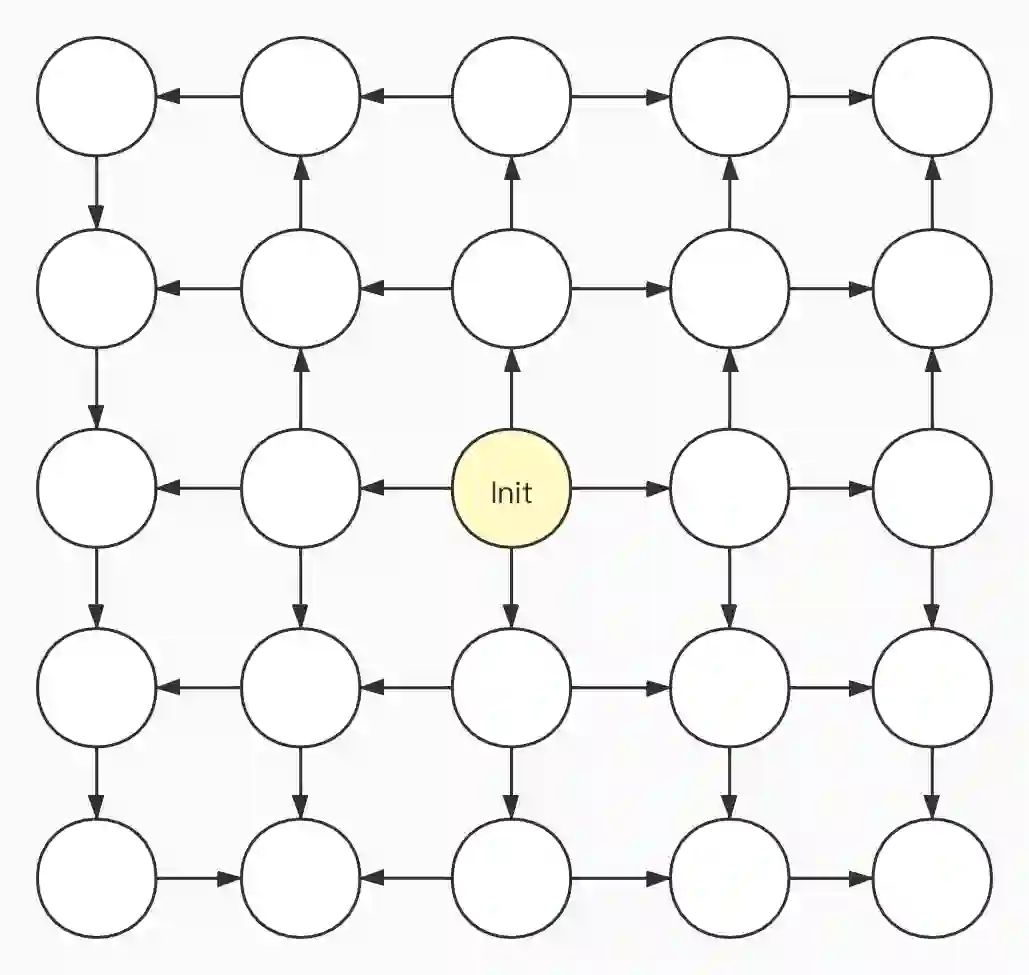
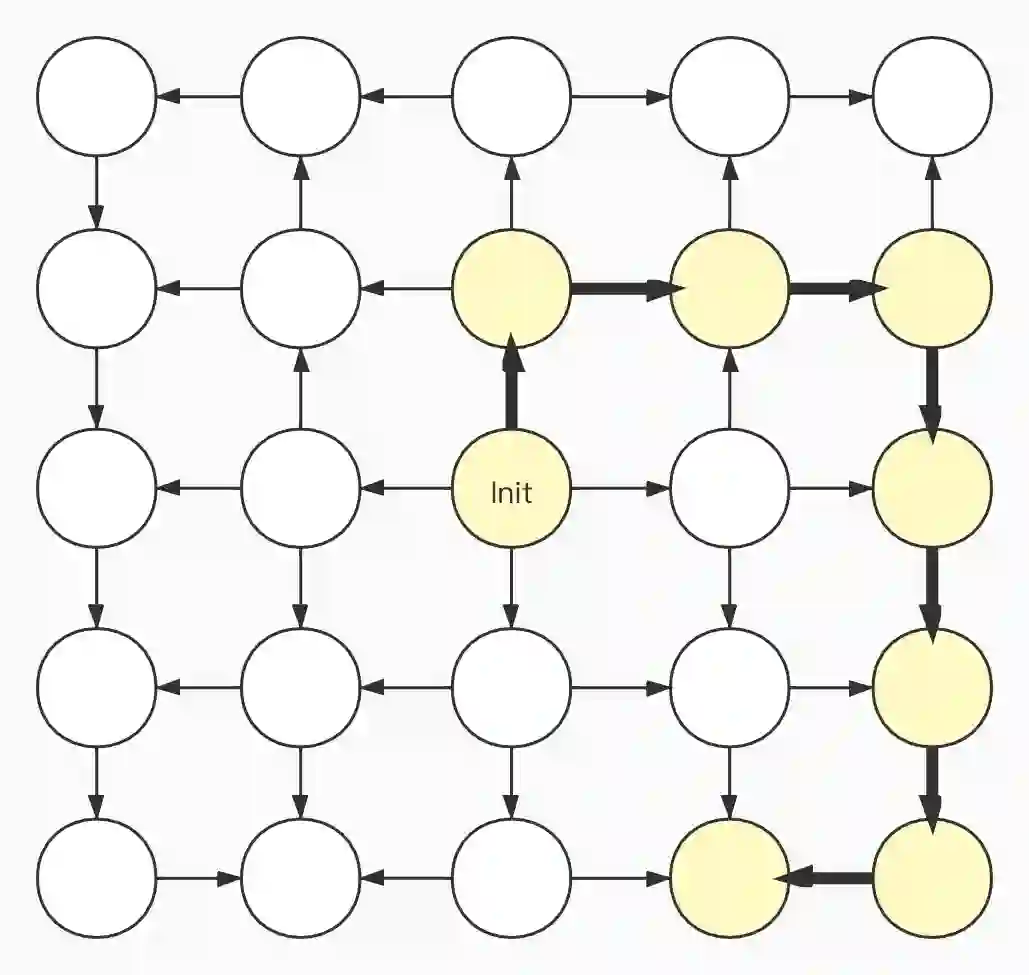
当我们能定义分布式系统全局状态改变之后，就可以进一步描述分布式系统的运行。分布式系统的运行可以看成是全局状态从某个初始状态 Init 起，一系列可能的改变过程。

具体系统的一次运行，只能从众多可能路径中选取一条，就像历史有无数种可能，但最终只有一次真实的演变路径一样。

4 使用数学语言精准刻画状态改变

这种状态图的思路很常见，也很好理解。比如，我们在下棋时，通常会在头脑中构造出一个全局状态转换图，然后选择最优的一条路径。如果可能的路径太多，还需要做剪枝优化。计算机博弈程序通常是这么设计的。这里的状态转换也可以叫“走法”，是固定的、简单的规则。比如对于中国象棋来讲，就是“马走日”“象走田”之类的规则。

而分布式系统的全局状态转换很难精确刻画，因为它太复杂了，需要使用具有极强描述能力的语言才行。是什么语言呢？对了，就是数学。因为数学是上帝用来描述宇宙的语言（这句话似乎是伽利略说的，无从考证）。数理逻辑和集合论是数学大厦的两座基石，这两大工具几乎是万能的，所以全局状态的改变也能用这两大工具来刻画。

Lamport 天才地提出了这种思想，而且重要的是，他精确定义了语法，同时实现了“数学编译器”，也就是 TLA+。于是我们就可以通过 TLA+ 语言来描述系统状态的转换了。

下面的例子是用 TLA+ 语言描述在 Paxos 协议中，Proposer 接收到 Accept 消息后做出的反应。

Phase2a(b) ==  /\ ~ \E m \in msgs : (m.type = "2a") /\ (m.bal = b)  /\ \E v \in Values :       /\ \E Q \in Quorums :            \E S \in SUBSET {m \in msgs : (m.type = "1b") /\ (m.bal = b)} :               /\ \A a \in Q : \E m \in S : m.acc = a               /\ \/ \A m \in S : m.maxVBal = -1                  \/ \E c \in 0..(b-1) :                        /\ \A m \in S : m.maxVBal =< c                        /\ \E m \in S : /\ m.maxVBal = c                                        /\ m.maxVal = v       /\ Send([type |-> "2a", bal |-> b, val |-> v])  /\ UNCHANGED <<maxBal, maxVBal, maxVal>>

下面的例子是 TLA+ 语言描述的在 Raft 协议中，节点更新 commit_index 时做出的反应。

AdvanceCommitIndex(i) ==    /\ state[i] = Leader    /\ LET \* The set of servers that agree up through index.           Agree(index) == {i} \cup {k \in Server :                                         matchIndex[i][k] >= index}           \* The maximum indexes for which a quorum agrees           agreeIndexes == {index \in 1..Len(log[i]) :                                Agree(index) \in Quorum}           \* New value for commitIndex'[i]           newCommitIndex ==              IF /\ agreeIndexes /= {}                 /\ log[i][Max(agreeIndexes)].term = currentTerm[i]              THEN                  Max(agreeIndexes)              ELSE                  commitIndex[i]       IN commitIndex' = [commitIndex EXCEPT ![i] = newCommitIndex]    /\ UNCHANGED <<messages, serverVars, candidateVars, leaderVars, log>>

5 属性判断

只描述系统状态转换用途不大。关键的是，我们想知道系统在各种可能发生的状态转换中，具备什么样的属性。同样，通过 TLA+ 可以描述某一时刻系统的状态。下面的例子就是 TLA+ 描述 Paxos 节点 value chosen 的语句。

VotedForIn(a, v, b) == \E m \in msgs : /\ m.type = "2b"                                       /\ m.val = v                                       /\ m.bal = b                                       /\ m.acc = a
ChosenIn(v, b) == \E Q \in Quorums :                     \A a \in Q : VotedForIn(a, v, b)
Chosen(v) == \E b \in Ballots : ChosenIn(v, b)

系统在每条可能的演化路径上，无非有如下几种情况：

某种属性从未发生
某种属性一直在发生
某种属性开始时发生了，某一时刻起又永远地消失了
某种属性一旦发生后，永远不会消失
某种属性时有时无
当属性 1 发生后，属性 2 就一直发生

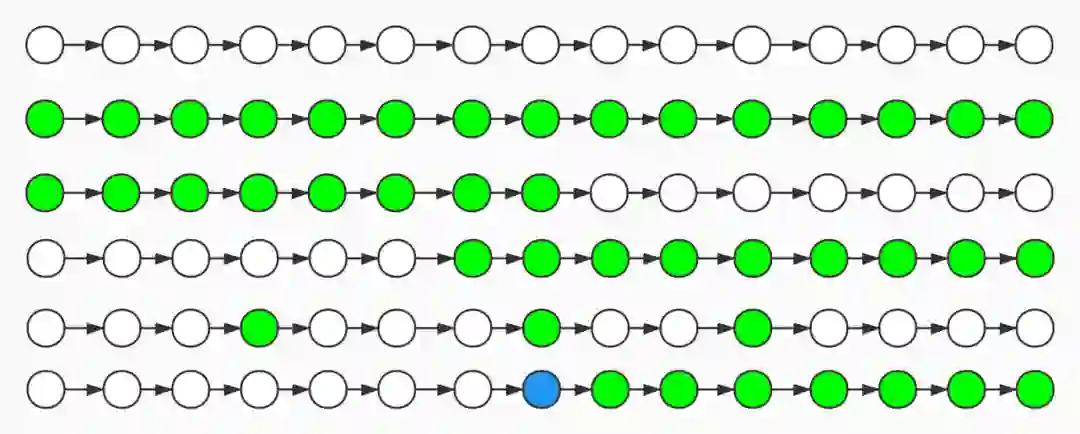
下图用带颜色的小球表示系统运行中的某个状态满足某种属性，大家稍微仔细看一下，应该不难理解其中的含义。

不变式（Invariance）

系统在每条可能的演化路径上，都具备的某种性质，称为不变式（Invariance）。比如 Paxos 的 single value chosen 不变式如下：

Consistency == \A v1, v2 \in Values : Chosen(v1) /\ Chosen(v2) => (v1 = v2)

也就是说，无论系统怎么运行，在任意时刻，系统的全局状态都会满足 Consistency 属性。

时序逻辑（Temporal Logic）

系统在某条路径的演化过程里，可以通过时序逻辑判断前后状态的关系。比如某一时刻某个 value 被 chosen，那么后续时刻，永远只有这一个 value 被 chosen。TLA+ 中的 TL，就是 Temporal Logic。时序逻辑比较复杂，这里就不展开了。后续用到时会详细介绍。

safety 与 liveness

safety 与 liveness 这两个名词经常出现在分布式理论的论文中，但却从来没有被精确定义过。通过 TLA+，可以很显然地看出它们的含义。同样，这里也不展开，后续用到时再详细介绍。

6 系统设计与验证

有了 TLA+，我们就可以大胆地设计分布式系统了。

我们可以先用 TLA+ 精确定义出系统，比如 Paxos、Raft，或者自己改造后的一些分布式算法。然后我们根据实际的运行场景和自己的要求，定义出若干检验条件，比如数据是否永远一致，系统中是否会出现双主等。最后，将定义好的模型和待检验条件扔进 TLC model checker。TLC model checker 会穷举系统每个可能的演化路径（内部会生成一张图，进行广度优先搜索），同时使用逻辑计算来判断状态的属性与状态之间的关系。如果某个属性不满足，系统就会报错，而且会给出这种错误在怎样的演化路径下会出现。如果模型通过了所有的检验，我们再用合适的编程语言把模型编程实现就可以了。

这时，开发者就可以非常自信地面对自己做出的系统了。就这样，分布式系统 corner case 这种几乎无解的难题，被 Lamport 老爷子使用数学工具给解决了。

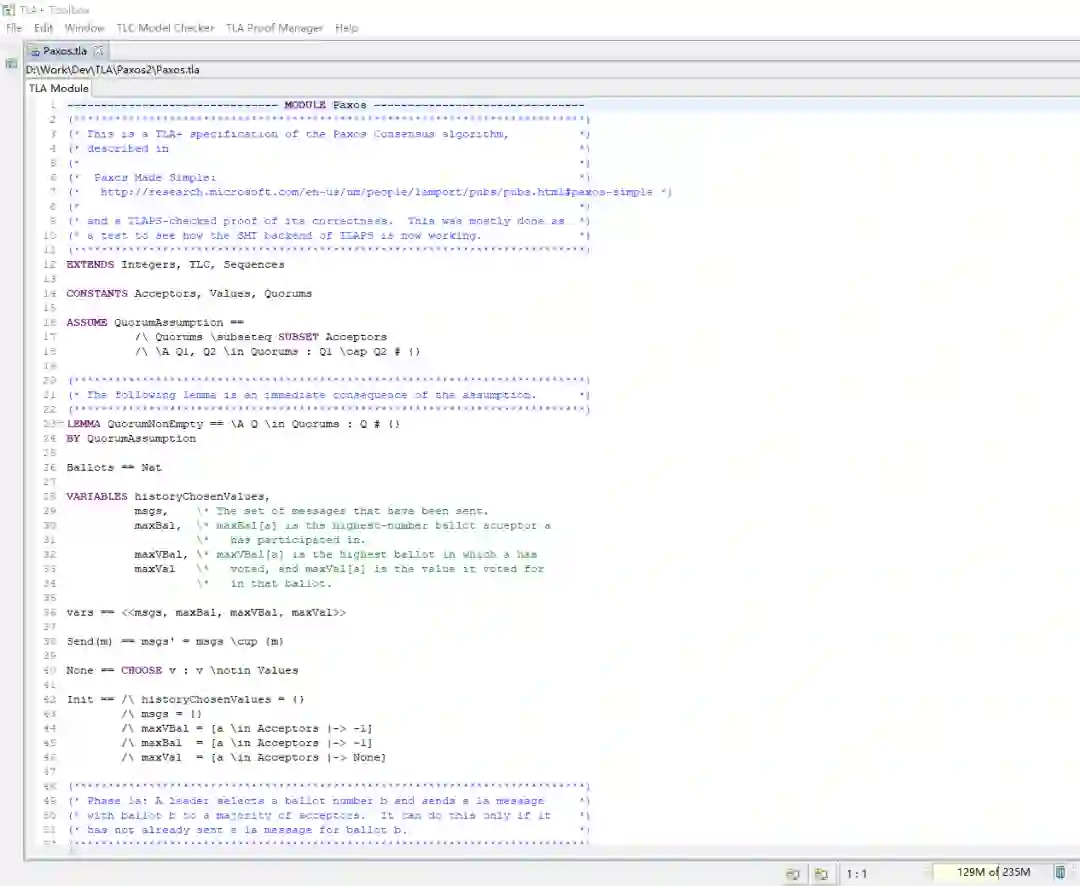
TLA+ Tools 截图如下：