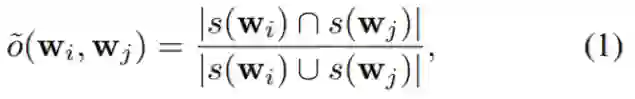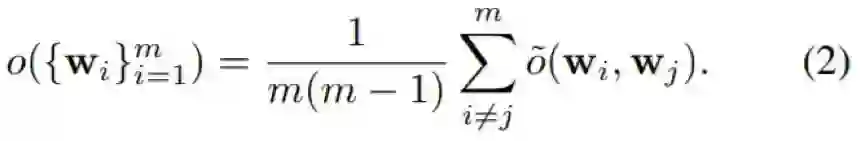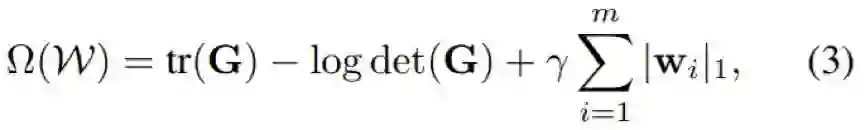ICML 2018 | Petuum提出新型正则化方法：非重叠促进型变量选择

2018 年 7 月 17 日 机器之心

选自arXiv

作者：John Olafenwa

机器之心编译

参与：Geek AI、路

第 35 届国际机器学习会议（ICML 2018）正在瑞典斯德哥尔摩举行。人工智能创业公司 Petuum 共有 5 篇论文入选，包含门控规划网络、变换自回归网络和无限可微分蒙特卡罗估计器等研究。本文将摘要介绍其中一篇论文《Nonoverlap-Promoting Variable Selection》，其中提出了一种有效的新型正则化方法，能够促进变量选择中的非重叠效应。

在评估模型质量的各种指标中，有两个比较常用：（1）在未曾见过的数据上的预测准确度；（2）对模型的解释。对于（2），科学家更喜欢更简单的模型，因为响应和协变量之间的关系更清晰。当预测量（predictor）的数量很大时，简约性问题就会变得尤其重要。当预测量的数量很大时，我们往往希望确定出一个能展现最强效果的小子集。

为了能在选择出重要因素的一个子集的同时得到准确的预测，研究者常常使用基于正则化的变量选择方法。其中最值得提及的是 L1 正则化（Tibshirani, 1996），这能促进模型系数变得稀疏。其变体包括 L1/L2 范数（Yuan & Lin, 2006），其中引入了组稀疏效应（group sparsity effect）和弹性网络（elastic net）（Zou & Hastie, 2005），这能强烈地促进大量预测量中互相相关的预测量共同进入或离开模型。

在很多机器学习问题中，都可以基于同一个协变量集预测出多种响应。比如，在多任务分类任务中，具有 m 个类别的分类器建立在一个共享的特征集之上，而且每个分类器都有一个类别特定的系数向量。在主题建模任务（Blei et al., 2003）中，可以在同一个词汇库上学习到多个主题，并且每个主题都有一个基于词的特有多项式分布。不同的响应与协变量的不同子集相关。比如，教育主题会与「学生」、「大学」和「教授」等词相关，而政治主题则会与「政府」、「总统」和「选举」等词相关。为了在执行变量选择时考虑到不同响应之间的差异，我们希望为不同响应选出的变量之间的重叠更少。

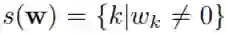
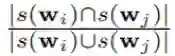
这个问题可用以下数学形式描述。设有 m 个响应共享 d 个协变量。每个响应都有一个特定的 d 维权重向量 w，其中每一维都对应于一个协变量。设为 w 的支撑集，索引了一个响应的所选变量。对于任意两个响应 i 和 j，我们希望它们的所选变量 s(wi) 和 s(wj) 有更少的重叠，其重叠度的衡量方式为。为了达到这个效果，我们提出了一种正则化器（regularizer），可同时促进不同的权重向量接近正交且每个向量变得稀疏，这能联合促使向量的支撑集的重叠更小。我们也通过实验表明：最小化该正则化器能够降低所选变量之间的重叠。

这项研究工作的主要贡献包括：

我们提出了一种新型正则化方法，能够促进变量选择中的非重叠效应。
我们将新提出的正则化器应用在了 4 种模型上：多类 logistic 回归、距离度量学习、稀疏编码和深度神经网络。
我们导出了求解这些正则化问题的有效算法。尤其值得提及的是，我们为正则化稀疏编码开发了一种基于 ADMM 和坐标下降（coordinate descent）的算法。
我们分析了新提出的正则化器能提升泛化性能的原因。
我们通过实验表明了这种正则化器的实际有效性。

方法

在这一节，我们提出了一种非重叠促进型正则化器，并将其应用在了 4 种机器学习模型上。

1 非重叠促进型正则化

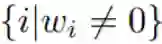
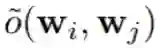
我们假设模型有 m 个响应，其中每一个都使用一个权重向量进行了参数化。对于向量 w，其支撑集 s(w) 定义为——w 中非零项的索引。而且这个支撑集包含所选变量的索引。我们首先定义一个分数来衡量两个响应的所选变量之间的重叠程度：

这是支撑集的 Jaccard 指数。越小，则两个所选变量的集合之间的重叠程度就越低。对于 m 个变量集，重叠分数则定义为各对分数之和：

这个分数函数不是平滑的，如果被用作正则化器会很难优化。我们则根据提出了一个平滑的函数，并且可以实现与 o(W) 相近的效果。其基本思想是：为了促进重叠较小，我们可以让（1）每个向量有少量非零项，（2）向量之间的支撑集的交集较小。为了实现（1），我们使用一个 L1 正则化器来促使向量变得稀疏。为了实现（2），我们促使向量接近正交状态。对于两个稀疏向量，如果它们接近正交，那么它们的支撑集将会落在不同的位置。这样能让支撑集的交集较小。

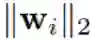
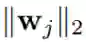
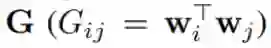
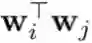
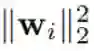
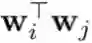
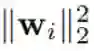
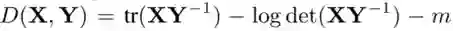
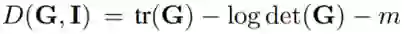
我们遵循了（Xie et al., 2017b）提出的方法来促进正交性。为了让两个向量 wi 和 wj 接近正交，可让它们的 L2 范数、接近 1，让它们的内积接近 0。基于此，就可通过促使这些向量的 Gram 矩阵接近于一个单位矩阵 I 来促进一组向量之间的正交性。因为 G 和 I 各自的对角线上没有了和 0，而分别是和 1，所以要让 G 接近 I，本质上就是让接近 0，让接近 1。由此，就促使 wi 和 wj 接近正交了。（Xie et al., 2017b）提出的一种用于衡量两个矩阵之间的「接近度」的方法是使用对数行列式散度（LDD：log-determinant divergence）（Kulis et al., 2009）。两个 m×m 正定矩阵 X 和 Y 之间的 LDD 定义为，其中 tr(·) 表示矩阵的迹。G 和 I 之间的接近度可以通过让它们的 LDD更小来得到。

将正交促进型 LDD 正则化器与稀疏度促进型 L1 正则化器组合到一起，我们就得到了以下 LDD-L1 正则化器：

其中 γ 是这两个正则化器之间的权衡参数。我们的实验已经验证，这种正则化器可以有效地促进非重叠。对（3）式和（2）式之间的关系的形式分析留待未来研究。值得提及的是，单独使用 L1 或 LDD 都不足以降低重叠。如图 1 所示，其中 (a) 是仅使用了 L1 的情况——尽管这两个向量是稀疏的，但它们的支撑集完全重叠。在 (b) 中仅使用了 LDD——尽管这两个向量非常接近正交，但因为它们是密集的，所以它们的支撑集完全重叠。(c) 中则使用了 LDD-L1 正则化器，这两个向量是稀疏的且接近正交。因此，它们的支撑集不重叠。

图 1：(a) 使用 L1 正则化的情况，向量是稀疏的但它们的支撑集重叠；(b) 使用 LDD 正则化的情况，向量是正交的但它们的支撑集重叠；(c) 使用 LDD-L1 正则化的情况，向量稀疏且互相正交，它们的支撑集不重叠。

2 案例研究

我们将 LDD-L1 正则化器应用在了 4 种机器学习模型上：

多类 logistic 回归（MLR）
距离度量学习（DML）
稀疏编码（SC）
深度神经网络（DNN）

3 算法

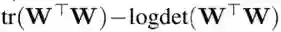
对于 LDD-L1 正则化的 MLR、NN 和 DML 问题，我们使用近端梯度下降（Parikh & Boyd, 2014）求解它们。这种近端操作针对的是 LDD-L1 中的 L1 正则化器。算法会迭代地执行以下三个步骤，直到收敛：（1）计算的梯度，其中 L(W) 是未正则化的机器学习模型的损失函数，是 LDD-L1 中的 LDD 正则化器；（2）执行 W 的梯度下降更新；（3）将 L1 正则化器的近端算子应用于 W。

算法 1：求解 LDD-L1-SC 问题的算法

实验

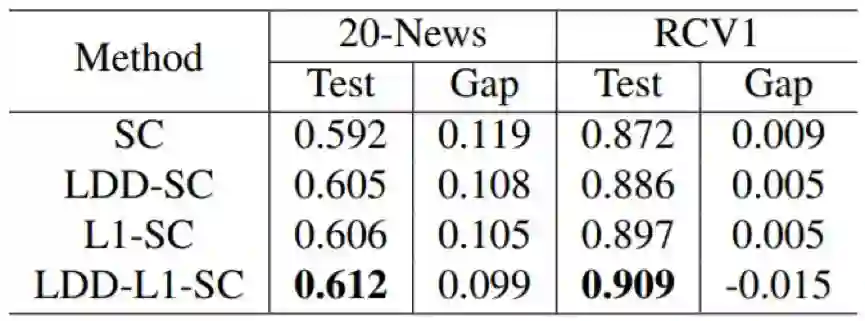
表 2：在 20-News 和 RCV1 的测试集上的分类准确度，以及训练准确度和测试准确度之间的差距

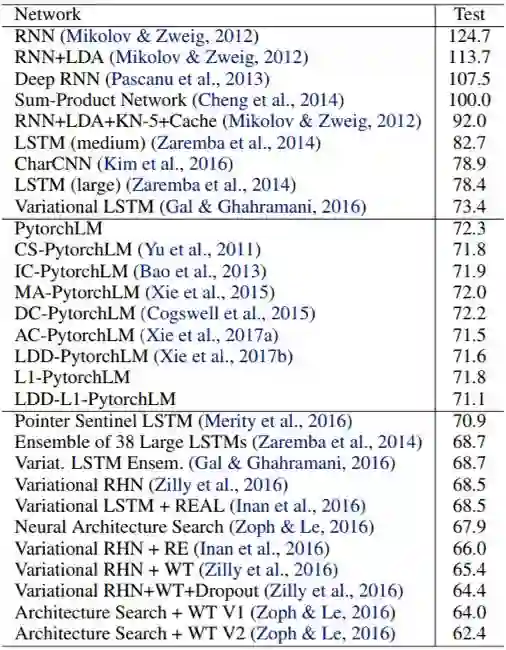
表 4：在 PTB 测试集上的词级困惑度

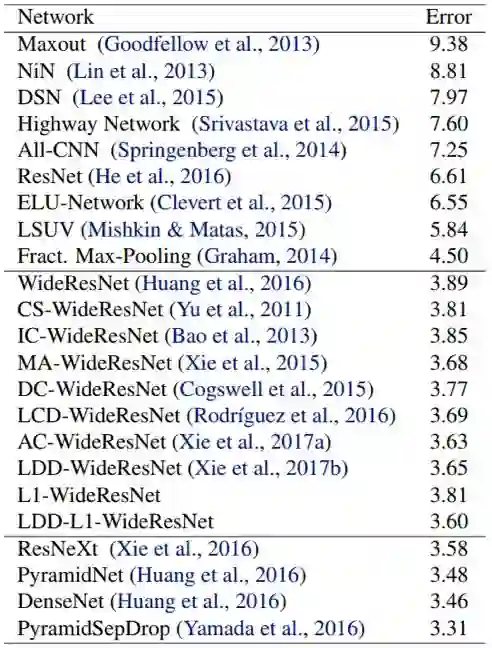
表 5：在 CIFAR-10 测试集上的分类误差（%）

论文：非重叠促进型变量选择（Nonoverlap-Promoting Variable Selection）

论文地址：http://proceedings.mlr.press/v80/xie18b/xie18b.pdf

变量选择是机器学习（ML）领域内的一个经典问题，在寻找重要的解释因素以及提升机器学习模型的泛化能力和可解释性方面有广泛的应用。在这篇论文中，我们研究了要基于同一个协变量集预测多个响应的模型的变量选择。因为每个响应都与一个特定协变量子集有关，所以我们希望不同响应的所选变量之间有较小的重叠。我们提出了一种能同时促进正交性和稀疏性的正则化器，这两者能共同带来降低重叠的效果。我们将这种正则化器应用到了 4 种模型实例上，并开发了求解正则化问题的有效算法。我们对新提出的正则化器可以降低泛化误差的原因进行了形式分析。我们在仿真研究和真实世界数据集上都进行了实验，结果表明我们提出的正则化器在选择更少重叠的变量和提升泛化性能上是有效的。