【优博微展2017】王乾：非结构网格紧致高精度有限体积方法

王乾：2017年清华大学优秀博士学位论文二等奖获得者

非结构网格紧致高精度有限体积方法

Compact High-Order Finite Volume Method on Unstructured Grids

作    者：王乾

指导教师：任玉新

培养院系：航天航空学院             

学    科：力学

读博感言：行胜于言，于平淡中见不凡。

研究背景/选题意义/研究价值

非结构网格高精度数值方法，在提高复杂工程流动问题精细模拟的计算效率方面具有很大的潜力。本文克服了传统非结构网格高精度有限体积方法模板巨大的瓶颈问题，发展了高效的非结构网格紧致高精度有限体积方法。论文选题具有重要的学术意义，同时具有重要的工程应用价值。

主要研究内容

紧致高精度有限体积方法的核心是紧致高精度重构。本文提出了能够在紧致模板上达到任意高阶精度的 “变分重构”方法。变分重构通过求解全局泛函极值问题，得到一个“最光滑”的分片多项式分布。相比于传统重构，变分重构最大的优势是其重构矩阵具有对称正定特性，因此重构矩阵是非奇异的，变分重构有唯一解。变分重构方程组是全场联立的大型稀疏线性方程组，采用Bock Gauss-Seidel等迭代方法求解。

本文提出了“重构和时间推进耦合迭代方案”来避免重构迭代造成的额外计算开销，提高基于隐式重构的有限体积方法的计算效率。我们将重构迭代和隐式双时间步法的迭代相耦合，在每个虚拟时间步只进行一次重构迭代。

另外，本文完善了非结构网格高精度有限体积方法求解体系，包括高阶网格变换、基于特征变量的限制器、粘性通量、高阶隐式时间推进等环节。

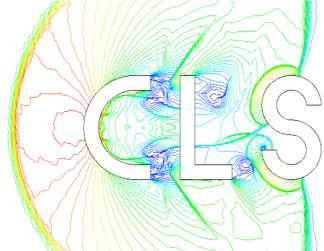
紧致有限体积方法模拟的复杂激波系结构

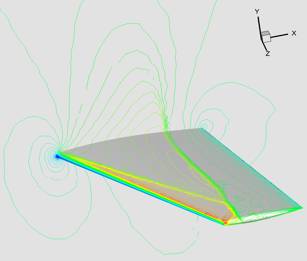
紧致有限体积方法模拟的ONERA-M6翼型跨声速绕流场

主要创新点

1、提出了能够在任意非结构网格上达到紧致高精度的“变分重构”，克服了传统高阶有限体积方法重构模板巨大的瓶颈问题。变分重构系数矩阵是对称正定的，保证了重构过程的可解性；

2、提出了隐式（双时间步）时间推进与基于迭代方法的重构过程耦合求解方案，保证了求解过程的高效率；

3、发展了与非结构网格高精度紧致有限体积方法匹配的实用求解技术，包括三维高阶网格处理、高阶边界条件、粘性项高阶计算方法、激波捕捉的限制技术等。以此为基础，发展了适用于任意混合网格的二维、三维非结构网格高精度紧致有限体积方法计算程序。

代表性学术发表

1、Wang Q, Ren Y X, Li W. Compact high order finite volume method on unstructured grids I: Basic formulations and one-dimensional schemes. Journal of Computational Physics, 2016, 314: 863-882. (SCI，IF:2.744)

2、Wang Q, Ren Y X, Li W. Compact high order finite volume method on unstructured grids II: Extension to two-dimensional Euler equations. Journal of Computational Physics, 2016, 314: 883-908. (SCI，IF:2.744)

3、Wang Q, Ren Y X, Pan J, et al. Compact high order finite volume method on unstructured grids III: Variationalreconstruction. Journal of Computational Physics, 2017, 337: 1-26. (SCI，IF:2.744)

作者：王乾

供图：王乾

编辑：清华大学研究生院  周明坤  严颖巧