北京电影学院发了一篇满是数学公式的计算机顶会论文，并开源了其代码（附链接）

来源：知乎专栏

本文约2400字，建议阅读5分钟。

这篇文章将介绍视觉特效在现代影视制作中稳定现象的产生方法。

大家都知道，视觉特效在现代的影视制作中出现十分频繁。

而诸如洪水、烟雾、爆炸等特效计算的背后，实际上是用计算机程序在求解已有百年历史的“纳维-斯托克斯方程”

这个方程，对于做流体动力学的读者一定不陌生，数十年来科学家们为了计算机翼升力，已将其研究了百千万遍。

然而基于影视制作的特别需求，影视科技工作者们对这个方程的求解提出了新的需求。

我们需要能够处理更大的时间步长以及不损失精度细节！！这两者本来是鱼与熊掌不可兼得，这就等于是在说：

于是伴随着特效应用的发展，十数年来，计算机图形学的科技工作者为了战胜这个问题不断地添砖加瓦，这里面比如就有大家耳熟能详的科研学府：斯坦福的科学家就曾经提出过使用涡旋力来增加流体的细节。

他们论文研究的算法，甚至直接和工业光魔合作，使用在当年星球大战特效镜头的制作上。

还有很多科研机构也是不断地在算法上推陈出新，甚至像迪士尼这样家里有矿的影视工作室还亲自上阵，不断地革新着美利坚的影视制作技术，带动起了好莱坞产、研结合的影视工具生态。

而不管是由工业光魔发表的用来补充烟火高精度细节的算法：

还是来源于迪士尼研究院-ETH Zurich的小波湍流论文：

都是不断在尝试攻克一个令人头疼的问题：如何在使用高效稳定的流体特效仿真算法前提下，尽可能地保证流体运动的细节，这最终落在了对于N-S方程中的对流部分的求解上。

 

在图形学特别是影视特效制作软件中，为了追求大时间步长的稳定性，对流方程的求解多采用半拉格朗日方法或其变种。这类方法虽然高效稳定，但有它最大的问题：数值粘性。

所谓数值粘性，顾名思义，就是物理系统中本不存在的粘性，是被人类设计的数值算法在求解方程的过程中带入系统的，与真实的物理事实相左。我们先领略一下“数值粘性” 会带来的问题：

比如我要沿着红线所示的速度和方向“对流”白色的方块

传统的对流算法由于数值粘性会使物质模糊掉

我们的算法尽大可能地避免了数值粘性， 保留了清晰地边界

流体的运动更为复杂，计算机算法保持清晰（守恒）的能力，就显得尤为重要。

这是一个由传统算法计算得到的烟雾动画，由于数值粘性的存在，烟雾的形态被过度地模糊了。

为了对抗这种过度平滑，科技工作者们提出了混合的粒子-网格方法，然而这类方法存在着计算速度慢，计算结果差强人意的缺陷：往往由于粒子的非连续性，流体的湍流运动会在粒子间拉出空隙，最终在视觉上产生噪声：

我们提出的算法既能最大可能地保持流体的湍流细节，又能维持流体场的连续性，有效地解决特效解算中这一老大难问题。

把三个方法的结果并排放在一起对比如下：

过度平滑的传统方法

计算耗时，且噪声过强的粒子方法

计算高效，即不失细节又平滑连续的我们的方法

为了以极高的清晰度来对流体中的物质场，我们给出了以下观察：

传统的对流算法直接作用于流体空间中的“物理量”，“数值粘性”于是会累加在“物理量”上，并最终造成“物理量”的模糊。

如果能构造出一个映射，使得流体场中的每一个空间点在任何时候都能知道自己初始时刻的位置并去初始时刻访问物理量的信息，我们就能够避免在对流的过程中累加“数值粘性”。

这个哲学像极了爱情：一切若只如初见，是多么的美好。

这个方法从求解的根本思路上跳出了传统对流方程求解方式：

• 以往的方法对流“物理量”

• 我们的方法对流“空间”本身

为此，我们定义了一个映射，这个映射的目的是将空间中的点映射回它初始时刻的位置 

因为流体运动而变化的空间映射的可视化

这个初始位置，满足如下的数学关系，称之为后向映射。 

在这个基础上，我们就有机会将原本的对流方程拆为空间的对流和物理量的重构两个部分。

为了便于重构物理量时对于积分项的计算，我们提出了整个算法中最至关重要的部分：前向映射。并给出了前向映射的演化方程:

有了前向映射，积分的过程变为了演化累加的过程（大大减少了计算量）

好了，小编保证，不会再有数学公式了！

我们将我们发明的这样层级前-后向映射来求解对流方程的形式称之为“n层级双向迹径映射对流求解法”（Bi-Directional Characteristic Mapping of Convective Quantaties of Level n BiMocq）。

虽然不打算在这里展开讨论，这样的做法使得在保持流体物理量守恒的同时还保证计算极为高效以及并行友好，大大地区别于混合的粒子-网格算法。我们粗暴实现的GPU代码可以对比相应的CPU的并发式代码加速50倍。

那么，BiMocq好处都有啥？

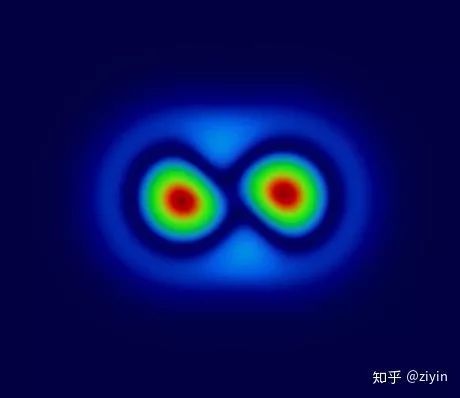
我们首先是对比了一个数学上有比较确定答案的问题，“泰勒涡旋”：两个初始状态如下的涡旋，在无粘的环境中，能量守恒的数值积分应该可以将其分开。

对此，我们实现并且对比了几乎所有主流使用的，先前发表于SIGGRAPH论文的算法，并验证了我们的算法在能量守恒上的优越性。

对比所有的SemiLagrangian类对流算法，BIMocqn 胜

BIMocqn特写

以及难以用Eulerian方法解算的leapfrogging vortex：

更进一步地，用一个简单的三维烟雾的例子来说明一下能量和质量守恒的好处：

该例子中，左边的是目前特效计算中常用的算法右边的是我们的新算法。由于数值粘性，以往的算法无法保证烟雾运动时的清晰形状导致了其在之后的效果计算中损失了烟雾的，湍流细节，那些更能体现烟雾真实感的卷曲细节。

大自然是最好的艺术家，我们想做的，仅仅是用程序在计算机中再现它的美。为此，我们用我们的数值算法在计算机中再现了如下场景，涡环相撞实验。

两个相对运动的涡环的实拍视频，在碰撞后会不断往直径方向扩大并最终由于任何微小的扰动在边缘处射出花瓣状的小涡。

这样的现象以往的数值算法存在数值粘性就根本不可能重现出来。

我们的算法成功地在计算机中再现了这个现象应该也是该领域第一次用高效的纯欧拉网格算法完整地再现了这个过程。

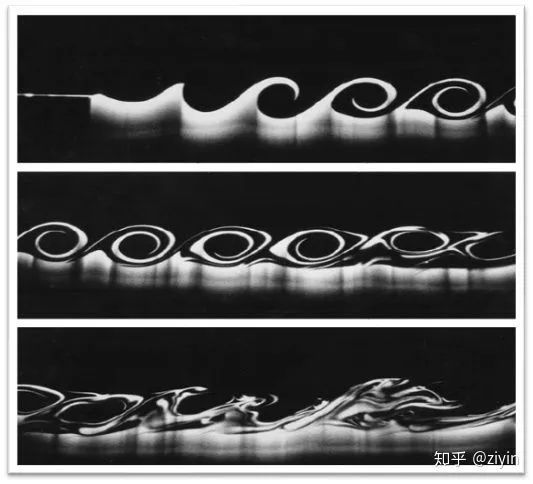
不知道有没有细心的朋友注意到过这样一种自然现象。

这种现象被称为开尔文-亥姆霍兹-瑞利-泰勒不稳定性(Kelvin–Helmholtz-Rayleigh-Taylor instability)，这种现象通常由于两种不同密度的流体在交界面处由于扰动而产生的不稳定现象。

同样，我们使用我们的算法对这个现象进行了近似的模拟。我们可以看到由于密度本身的对流会对整个流场产生影响，对比以往的数值算法，在同等分辨率下由于我们的算法对密度对流有着更准确的估计，因此我们也能更准确地模拟这种不稳定性带来的涡结构。

作为展示这个算法在更通用的特效环境中的使用我们也增加了使用我们提出的新算法生成的爆炸以及汽车漂移特效的案例。

代码Github地址：

https://link.zhihu.com/?target=https%3A//

github.com/ziyinq/Bimocq

原文链接：

https://zhuanlan.zhihu.com/p/72916159

编辑：于腾凯

校对：杨学俊