本文为大家介绍了如何使用计算学习理论研究机器学习任务和方法,并对其中比较重要的子领域PAC学习以及VC维进行了简要介绍。
计算学习理论,或者说统计学习理论,指的是量化学习任务和算法的数学框架。
对于机器学习领域的实践者来说,想找到大多数问题的优质解决方案,并不需要深度了解这些机器学习的子领域。尽管如此,在子领域中,对一些更重要的方法有一个较高水平的理解可能为数据中学习的更广泛的任务中提供洞见。
在本文中,你将会发现一个对机器学习的计算学习理论的简要介绍。
-
计算学习理论使用形式化的方法研究学习任务和学习算法
-
PAC 学习提供了一个可以量化机器学习任务计算难度的方法
-
VC维提供了一种可以量化机器学习算法计算能力的方法
![]()
计算学习理论(https://en.wikipedia.org/wiki/Computational_learning_theory),或者简称CoLT,是与应用于学习系统的形式化的数学方法的使用有关的研究领域。
它致力于寻找理论计算机科学工具来量化学习问题,包括刻画学习特定任务的难度。
计算学习理论可能被认为是统计学习理论(或者简称SLT,https://en.wikipedia.org/wiki/Statistical_learning_theory)的延伸或者说是兄弟,两者都是使用形式化的方法来量化学习算法。
学习任务和学习算法之间的区分是十分武断的,并且在实践中,这两个领域有很多重叠之处。
“当你考虑到学习器的计算复杂度之后,就可以对统计学习理论进行扩展,从而得到一个新领域。这个领域被叫做计算学习理论或COLT。”
“……一个叫做计算学习理论的理论框架,有时也被叫做统计学习理论。”
计算学习理论主要关注于监督学习任务。实际问题和实际算法的形式化分析非常具有挑战性。因此,通常通过关注二分类任务甚至简单的基于规则的二分类系统来降低分析的复杂度。因而对于实际问题或算法的解释,公理的应用可能是有限且具有挑战性的。
“在学习中,未被解决的主要问题是:我们如何确定我们的学习算法已经有一个会预测之前前未知输入的正确值的假设呢?”
——第713页,《人工智能:一种现代方法》,第三版,2009
作为一个机器学习的实践者,知道计算学习理论以及一些主要的研究领域是非常有用的。这个领域为我们在数据上拟合模型时试图实现的目标提供了有用的基础,也可以提供对方法的洞见。
该研究有很多子领域,虽然计算学习理论研究中最常讨论的两个领域是:
简单来说,我们可以将PAC学习叫做机器学习问题的理论,将VC维叫做机器学习算法的理论。
作为一个实践者来说,以上提到的话题你可能都会遇到,那么对它们进行初步的了解则是非常有必要的。让我们仔细看一下。
如果你可以更加深入计算学习理论的领域,我推荐你看这本书。
概率近似正确学习(Probably approximatelycorrect learning)或者叫做PAC学习,指的是由Leslie Valiant提出的理论性的机器学习框架。
PAC学旨在把学习任务的难度量化,可以被认为是计算学习理论的首要子领域。
考虑到在监督学习中,我们试图去近似一个未知的从输入到输出的潜在映射函数。我们不知道这个映射函数是什么样的,但是我们假设它存在,并且我们具备一些由此函数生成的数据样本。
PAC学习与查找未知目标函数接近的假设(拟合模型)所需的计算量有关。
更多关于在机器学习中使用“假设”适用于拟合模型的内容,请参考这个教程:
-
什么是机器学习中的“假设”(https://machinelearningmastery.com/what-is-a-hypothesis-in-machine-learning/)?
我们的想法是一个差的假设会通过它在新的数据集上预测的结果表现出来,例如,基于它的泛化误差。
当一个假设可以使得大部分或者大量的预测结果正确时,例如,一个小的泛化误差就很可能是对目标函数好的近似。
“计算学习理论奠基的原理是,在输入少量样本后,任何严重错误的假设几乎一定会以较高的概率被“找出来”,因为它可能会做出不正确的预测。因此,任何与足够大的训练数据集一致的假设不可能错很多:也就是说,它必定是概率近似正确的。”
——第714页,《人工智能:一种现代方法》,第三版,2009
这种概率性的语言给了这个定理起了名字:“概率近似正确”。也就是说,一个假设试图“近似”一个目标函数,并且如果它的泛化误差较低,该假设“很可能”是非常不错的。
使用形式化的方法,可以确定一个监督学习任务的最小泛化误差。然后,该定理可用于从问题领域中估计期望样本的数量,这会被用来确定一个假设是否为PAC。也就是说,它为寻找PAC假设而估计样本的数量提供了一种方法。
“PAC框架的目标是了解要想获得良好的泛化结果需要多大的数据集。它也为学习的计算成本提供了边界……”
除此之外,如果一个算法可以在多项式时间(polynomial time)内找到一个PAC假设,那么该假设空间(机器学习算法)在PAC框架下是高效的。
“如果有一个多项式时间算法能够识别出一个函数是 PAC的,那么我们就说这个假设空间是高效的PAC可学习。”
关于PAC学习更多的知识,可以参考这个话题的开创性书籍:
Vapnik–Chervonenkis理论,简称VC理论,指的是由 Vladimir Vapnik 和 AlexeyChervonenkis提出的理论的机器学习框架。
VC理论试图将学习算法的能力进行量化,并被认为是统计学习理论首要的子领域。
VC理论涉及到很多内容,最引人注目的是VC维。VC维将假设空间的复杂度量化,例如,给定一个表征和学习算法,模型可被拟合。
一种考量假设空间(可被拟合的模型空间)复杂度的方法是基于它所包含的不同假设的数量以及也许是操作空间的方式。VC维是一种非常巧妙的方法,它替代了目标问题的样本数量,这些样本可以通过空间假设来区分。
“VC维通过使用H完全区分X不同实例的数量来衡量假设空间的复杂度[……]”
VC维估计了对特定数据集的分类机器学习算法的能力或容量(样本的数量和维数)。
形式化地说,VC维是来自算法可以“打散”的假设空间中训练集的最大样本数 。
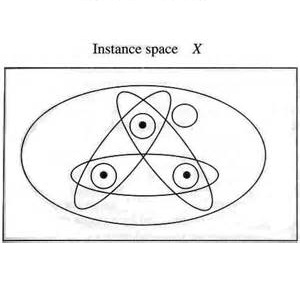
“定义在实例空间X上的假设空间H的Vapnik-Chervonenkis维度, 也就是VC(H),,是可被H打散的X的最大有限子集的大小”。
无论是打散还是被打散的集合,在数据集当中,都意味着特征空间中的点可以通过空间中的假设被选择或彼此分离,从而使各个组的样本的标签是正确的(无论它们是什么)。
一组点是否可以被一个算法打散取决于假设空间和点的数量。例如,一条线(假设空间)可被用于打散三个点,但是却不能用于四个点。
在带有类标签0或1的二维平面上,任何放置的三个点都可以被标签用一条线“正确”分割,例如,打散。但是,平面上带有二分类标签的放置的4个点则不能通过一条线进行正确划分,例如,不能被打散。取而代之的是另一种算法,例如椭圆。
![]()
因此,机器学习算法的VC维是算法的特定配置(超参数)或特定的拟合模型可以打散的数据集中最多点的数量。
在所有情况下,预测相同值的分类器将会有一个值为0的VC维,也就是没有点。较大的VC维表明算法非常灵活,尽管灵活性可能会以过拟合的额外风险作为代价。
PAC学习中的一个关键量是Vapnik-Chervonenkis 维,即VC维,它可以衡量函数空间的复杂度,并且可以将PAC框架扩展到包含无数函数的空间。
了解更多关于PAC学习的知识,可参这个主题的开创性书籍:
扩展阅读
如果您想深入了解这个主题,本节提供了更多相关资源。
《概率近似正确:在复杂世界学习和繁荣的自然算法》,2013
《人工智能:一种现代方法》,第三版,2009
《计算学习理论导论》,1994
《机器学习:概率的视角》,2012
《统计学习理论的本质》,1999
《模式识别与机器学习》,2006
《机器学习》,1997
统计学习理论(https://en.wikipedia.org/wiki/Statistical_learning_theory),维基百科
计算学习理论(https://en.wikipedia.org/wiki/Computational_learning_theory),维基百科
概率近似正确学习(https://en.wikipedia.org/wiki/Probably_approximately_correct_learning),维基百科
Vapnik–Chervonenkis理论(https://en.wikipedia.org/wiki/Vapnik%E2%80%93Chervonenkis_theory),维基百科
Vapnik–Chervonenkis维度(https://en.wikipedia.org/wiki/Vapnik%E2%80%93Chervonenkis_dimension),维基百科
总结
本文当中,你会了解到关于机器学习的计算学习理论的基本知识。
-
计算学习理论使用形式化的方法来研究学习任务和学习算法;
-
PAC学习提供了一种量化机器学习任务计算难度的方法;
-
VC维提供了一种可以量化机器学习算法计算能力的方法。
如果有任何问题,可以在下方评论,我将会尽可能地做出解答。
原文标题:
A Gentle Introduction toComputational Learning Theory
原文链接:
https://machinelearningmastery.com/introduction-to-computational-learning-theory/
陈超,北京大学应用心理硕士在读。本科曾混迹于计算机专业,后又在心理学的道路上不懈求索。越来越发现数据分析和编程已然成为了两门必修的生存技能,因此在日常生活中尽一切努力更好地去接触和了解相关知识,但前路漫漫,我仍在路上。