【从复数开始的科技文明II】- 文化脉络中的数学 10

会员服务 ·

【从复数开始的科技文明II】- 文化脉络中的数学 10

2017 年 8 月 20 日 遇见数学 单维彰

以下视频自单维彰教授Youtube账户

已经得到单老师授权许可, 这里表示诚挚的感谢!!

编辑|设计: 李想

单维彰教授, 美国宾州州立大学博士, 台湾的中央大学师资培育中心与数学系合聘副教授.

"我以中国式的知识份子为己任"

「结合律的出现」

从此代数有了全新的视野

抽象代数的滥觞

据汉弥尔顿的日记，他在都柏林附近的Brougham桥（金雀花桥）上获得四元数的灵感。如今，桥上树立一块纪念此事的碑，而碑文上刻著的一条等式 ijk=-1 就表现了结合律.

事实上，「结合律」这个名词就是在哈密尔顿讨论四元数的时候首度出现。在四元数之前，数学家并没有讨论过不满足结合律或交换律的运算；也就是从四元数开始，数学的「代数」支系有了全新的视野：人们可以在一个全然人造的符号系统中定义加减乘除，并讨论其运算性质。

现在，我们应该可以不过份失真地诠释哈密尔顿发展四元数的心理状态：他要找到一种和直线数（实数）与平面数（复数）都相容的空间数。后人评判哈密尔顿是英国仅次于牛顿的伟大数学家；而且，也像牛顿一样，他的物理学家身份可能更胜于數学家。但是，在四元数上，哈密尔顿是一位道道地地的纯数学家：他最关心的是数学内部的一致性，或者說是数学的「美」。

哈密尔顿虽然也全面地在物理上示范四元数的应用，范围包括当时所知的流体力学、热力学和光学（他在这些物理课题上已经声名卓著），但是这些示范并没有产生新的物理知识，也没有简化原來的理论和计算，事实上可能还为了一致性的美而付出更高的计算代价。真正可以仰仗四元数而发展的物理观念，在哈密尔顿身故 (1865) 之后才发生，那就是麦克斯韦 (James Maxwell, 1831—79) 的电磁理论。

詹姆斯·克拉克·麦克斯韦(James Clerk Maxwell)

詹姆斯·克拉克·麦克斯韦(1831.6.13－1879.11.5)，苏格兰数学物理学家, 其最大功绩是提出了将电、磁、光统归为电磁场中现象的麦克斯韦方程组.

在麦克斯韦于1873年出版的画时代著作《电磁通论》(A Treatise on Electricity and Magnetism) 里面的数学，的确是四元数，但是麦克斯韦也不厌其烦地阐述「笛卡儿方法」，也就是分别描述x坐标、y坐标和z坐标的方程式，并且不止一次提到：如果能将纯量和向量的计算分开来做，应该会更简洁，而且更直接对应物理意义。

麦克斯韦出版《电磁通论》之后短短六年就过世了，来不及实现他心目中更「简洁」的向量数学。这份著作引领了许多跟随者，包括美国耶魯大学的吉布斯教授 (Willard Gibbs, 1839—1903) 和英国的自学天才亥维赛 (Oliver Heaviside, 1850—1925).

约西亚·威拉德·吉布斯(Josiah Willard Gibbs)

吉布斯(1839年2月11日－1903年4月28日)是一位美国科学家. 他在物理学、化学以及数学领域都做出了重大的理论贡献。吉布斯还将麦克斯韦方程组引入物理光学的研究, 并与英国科学家奥利弗·亥维赛各自独立发展了现代矢量分析理论.

吉布斯读《电磁通论》的时候已经是教授而且已经发表了重要的物理论文，但是他读了这本书之后才开始学习四元数，当作研究电磁学的工具。过程中他洞察四元数有「多余的」性质可以略去，只要汲取向量的标量乘法(台:系数积)、内积、外积和一些我们在大一微积分课程中学习的微分与积分的运算，就能描述电磁现象并据以计算和推论。吉布斯从1877年起开授电磁学课程，在课堂上采用他发展的向量方法；后來，他在1881年自费印刷了向量讲义，除了课堂使用以外，陆续邮寄了大约130份给欧美各地的同行。二十年后的1901年，总算由他的学生Wilson代笔撰写并正式出版为《向量分析》(Vector Analysis) 教科书.

奥利弗·亥维赛(Oliver Heaviside)

亥维赛(1850年5月18日－1925年2月3日)英国自学成才的物理学家, 在电磁学上举足轻重的麦克斯韦方程组重新表述，由四元数改为矢量，将原来20条方程减到4条微分方程.

亥维赛讀《电磁通论》》的时候是一位失学而且无业的24岁「啃老族」，他决定要自修成为一名电磁学家。他同样是为了研究电磁学而学习四元数，也同样将四元数「去芜存菁」成空间向量及其运算，并应用在他1883年发表的电磁学论文里。当他在1888年拿到吉布斯的讲义时，赫然发现他们发展了完全一样的向量方法。但是这两人从來不曾争论谁先谁后，或许他们是当时世界上唯二的向量推手，必须惺惺相惜吧.

「寻找最好形式的空间数」

尽管向量的计算规则如此之「丑」，物理学者和其他的科学家终究因为实用性而选择了它

实用为王 - 不美总比不妙好

相对于四元数，空间向量并不相容于实数，也不能自成一个代数系统。向量内积的结果不再是向量，所以内积不是向量乘法；而外积的结果虽然是向量，却不满足结合律.

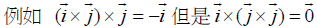
会有非零向量之外积是零向量的窘况（任兩个平行向量的外积是零向量）。尽管向量的计算规则如此之「丑」，物理学者和其他的科学家终究因为实用性而选择了它.

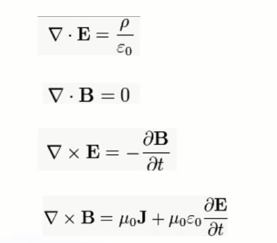
△麦克斯韦方程组使用向量描述而简洁太多

向量解开了坐标的秘密

复数平面揭开了平面向量的原型，坐标不再只是被动地记录点的位置，释放了坐标本身的威力. 就像物理学家解开了原子的秘密一样威力巨大而影响深远.

哈密尔顿遗漏了什么吗?

至于哈密尔顿，他有更好的选择吗？他是不是没有找到最好的空间数形式？有没有更妙的空间数等著我们这些后人发掘呢？简单地說：没有了。霍维茨 (Adolf Hurwitz, 1859—1919) 在1898年证明：在合理的条件下，所有的「数系」只有四种：实数、复数、四元數，和一种相当于是由四元数所造成的复数。所以，哈密尔顿毕竟是位大师级的数学家，他之所以没想到更妙的形式，是因为它根本不存在.