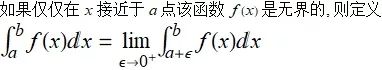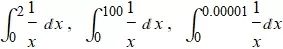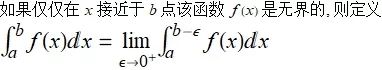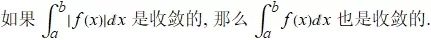【反常积分】图解普林斯顿微积分 15

第20 章 反常积分：基本概念(Improper Integrals: Basic Concepts)

反常积分是普通定积分的推广，指含有无穷上限/下限，或者被积函数含有瑕点的积分, 本章的内容:

• 反常积分、收敛和发散的定义;

• 关于没有边界区域的反常积分;

• 关于比较判别法、极限比较判别法、p 判别法和绝对收敛判别法的理论基础.

20.1 收敛和发散(Convergence and Divergence)

如果积分 ${\int }_a^b\text{f(x)dx}$ 中 f 不是有界的: 当 x 在区间 [a,b] 内, 函数 f 在区间有一条垂直渐近线的时候, 函数会在渐近线附近变得很大, 且没有界限, 这就使该积分成了反常积分(improper).

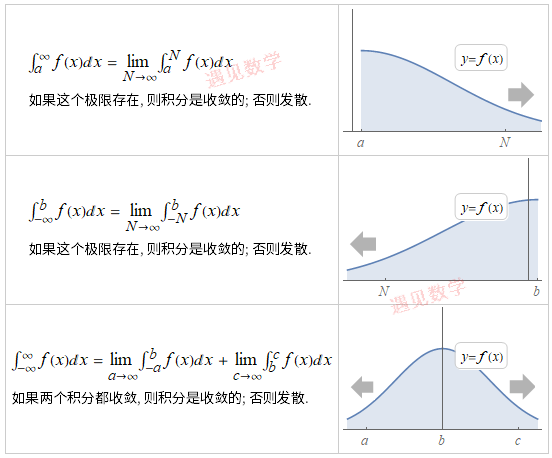
积分区间如果是无界的, 如 [0,∞) 或 (-∞,∞), 也使这个积分为反常积分.

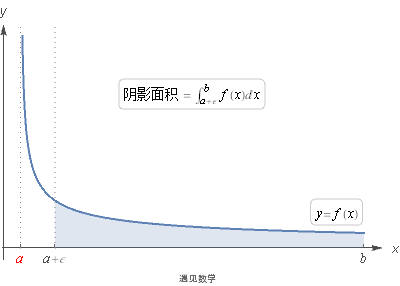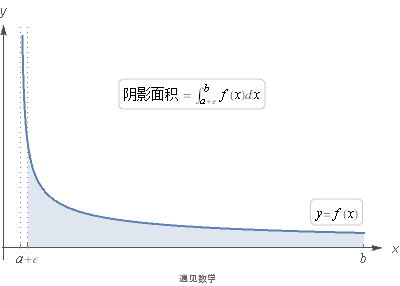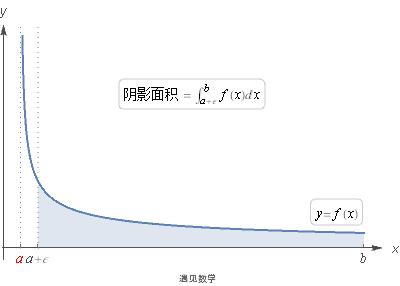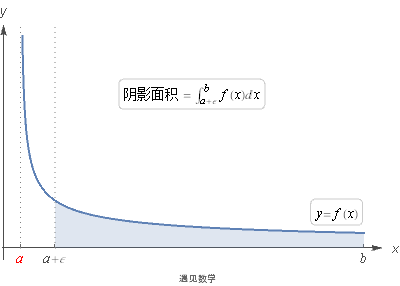
先来看第一种情况的图形:

为了研究什么情况下一块无限区域的面积会是有限的, 我们需要使用极限. 观察下面动图:

数 ε 越小, 我们对这块无限区域的估算就越接近于真实值, 也就是当在 x=a 处有破裂点有:

如果能找到这样的极限, 我们就说这个积分收敛; 否则认为该积分发散.

在实际中, 如果你知道积分是收敛的, 可以通过算法求得收敛值. 如果积分是发散的, 就要小心处理了.

20.1.1 反常积分的一些例子

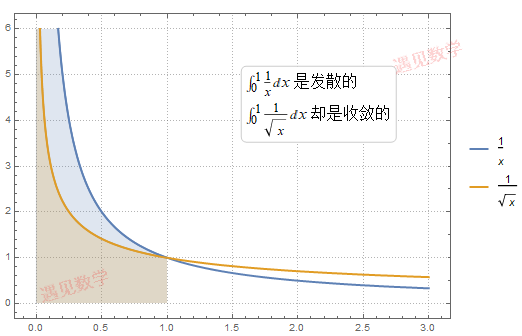
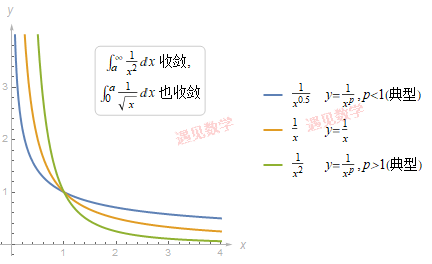
考虑下面两个反常积分, 被积函数非常相似, 在 x=0 点都有垂直渐近线, 但一个是发散而另一个是收敛的, 现在观察图形.

$\frac{1}{\sqrt{x}}$ 的图像足够接近于 y 轴, 所以它所对应的积分是收敛的; 而 $\frac{1}{x}$ 没有那么接近于 y 轴, 所以它对应的积分是发散的. 但是对于所有 x=0 点有渐近线的函数, 很难区分, 需要分别对待每个积分.

一个反常积分在有界区间的收敛和发散是由接近破裂点的走势决定的, 所以下面几个积分都是发散的.

20.1.2 其他破裂点

如果函数 f 在区间 [a,b] 内有破裂点 c, 需要把这个积分分成两部分 [a,c] 和 [c,d], 并且只有当这两部分积分都收敛时候, 对 f 的积分才是收敛的. 如果任何一个发散, 那么整个积分都是发散的.

为计算反常积分, 如果必要就把它分解. 每一部分最多只能有一个瑕点(problem spot), 而且该点要在积分的上下限上.

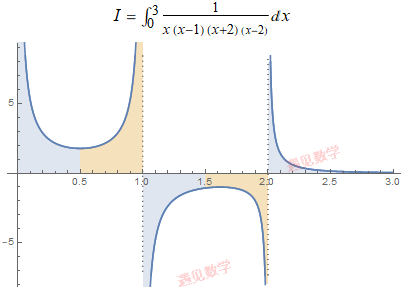
下面反常积分在积分区间的瑕点是 x=0,1,2 , 就需要在这些瑕点之间选择一些数如 $\frac{1}{2}$和 $\frac{3}{2}$, 把原始的积分分成下面 5 个积分:

现在 5 个积分的瑕点都不超过一个, 可以分别进行分析. 但这5 个积分没有一个是收敛的!

20.2 关于无穷区间上的积分(Integrals over Unbounded Regions)

现在看当积分上下限有一个或同是无穷时的情况; 也就是说, 积分区间是无界的(unbounded). 用符号表示:

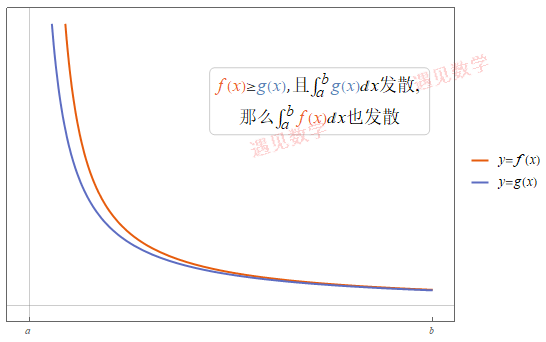
20.3 比较判别法(理论)The Comparison Test

20.4 极限比较判别法(理论)The Limit Comparison Test

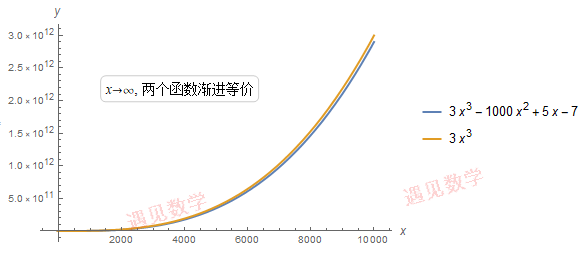
极限比较判别法需要两个近似的函数, 如两个函数在 x=a 是非常接近, 那么它们收敛或发散的行为是相同的.

20.4.1 函数互为渐近线

实际上, 可以对渐近等价函数做相乘, 相除, 幂运算或变量替换都是适用的. 但加减关系并不适用!

20.4.2 关于判别法的陈述

如果积分函数 f(x), 它的瑕点仅仅在 a 点, 那么反常积分收敛还是发散, 如果能找到一个渐进函数 g(x) 进行判别, 即 g 的结论也适用于 f 函数. 比如下面例子:

20.5 p 判别法(理论)

上面两种判别法基本策略都是选择一个能与函数 f 相比较的函数 g, 并且 g 相比 f 会更容易判别收敛性. 最常用的 g 函数是 $x^{-p}$ , 其中 p>0.

事实上只要记住 $\frac{1}{x^2}$ 和 $\frac{1}{\sqrt{x}}$ 就能理解掌握上面的情况:

20.6 绝对收敛判别法

(完)

「予人玫瑰, 手留余香」

和自己最好的朋友们一起来遇见数学!