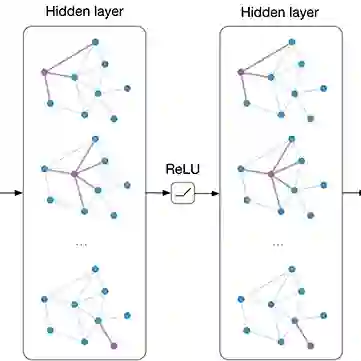
【GNN】JK-Net：深层 GNN 架构

2020 年 6 月 11 日 AINLP

今天学习的是 MIT 同学 2018 年的论文《Representation Learning on Graphs with Jumping Knowledge Networks》，发表于 ICML，目前共有 140 多次引用。

目前的图表示学习都遵循着领域聚合的方式，但这种方式的层数无法增加，kipf 的 GCN 使用了两层模型，随着深度增加会出现 over-smooth 的问题，导致性能下降。

为了更好的学习邻居的结合和属性，作者提出了一种叫跳跃知识的网络（Jumping Knowledge Networks）架构，并在诸多数据集中取得了 SOTA 的成绩。

此外，JK 架构可以与现有的卷积网络（如 GraphSAGE、GAT 等）模型相结合，可以用于改善这些模型的性能。

1.Introduction

目前基于聚合方式的 GCN 最好的性能是 2 层，更深的层数会降低模型性能。在计算机视觉中，残差连接可以解决类似的学习能力退化的问题，并且极大的帮助了深度模型的训练。但是即使使用了残差链接，GCN 也没法增加层数，相关的工作有：citation network。

为此，作者研究了目前基于领域聚合方式的性质和局限性。

作者针对随机游走进行研究，并发现：除节点特征以外，节点的子图结构（也可以理解为所处位置）会极大的影响领域聚合的效果。下图展示了 GooglePlus 的社交网络，从正方形节点开始进行 n-step 的随机游走：

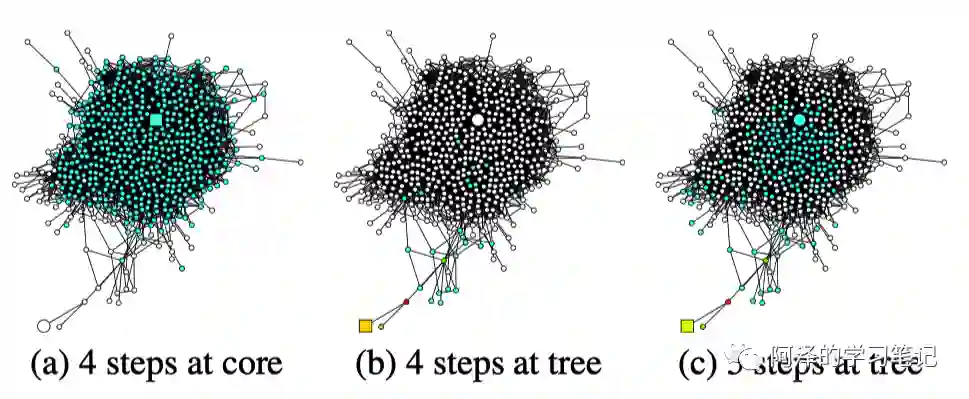
我们可以从（a）中看到，处在中心节点位置的正方形节点经过 4-step 就可以涵盖整个图；而（b）中，处在边缘节点位置的正方形节点，经过 4-step 仅仅扩展了一小部分，经过 5-step 达到核心后才迅速蔓延。

这表明：即使在同一张图中，相同步数也会导致不同的效果。在实际应用中，我们应该通过组合不同形式的 n-step 来控制不同节点的扩散速度。

随后，作者又证明了 k 层 GCN 的影响和随机游走 k 步的影响近似相同。（证明方式见论文）

下图展示 k 层 GCN 和 k 步随机游走的结果，颜色深表示影响概率越高。

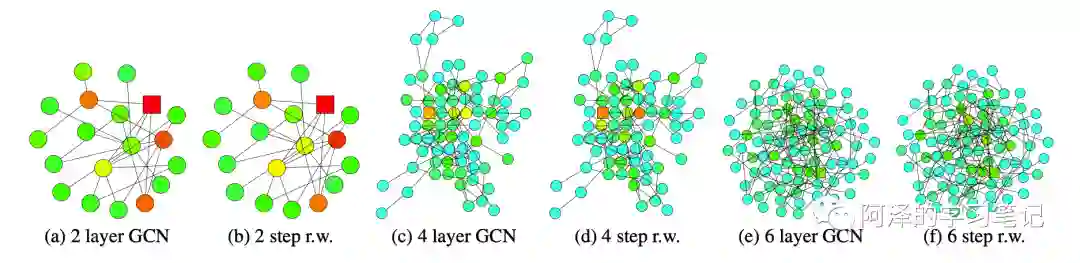
下图展示了带有残差的 GCN 的影响分布，与惰性随机游走更加相似。

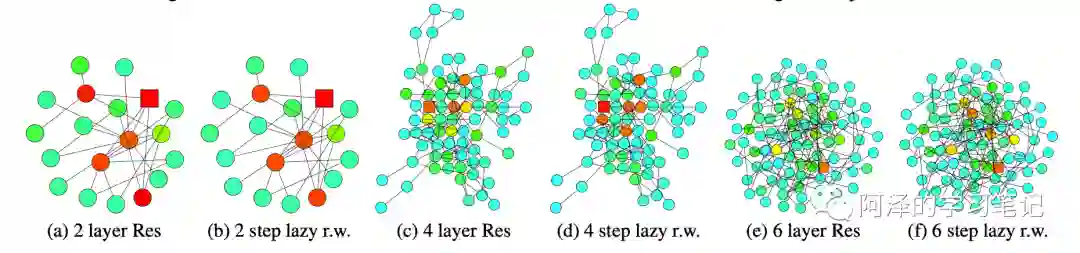
可以看到，带有残差的 GCN 导致每一步都有更高的概率停留在当前节点，这与节点多样化需求相违背。

回顾我们看到的第一场图，如果 GCN 使用相同的层数，其与施加固定 step 的随机游走会有相同的效果。相同的层数可能会导致中心区域的节点表示失去局部信息，但却会让边缘节点探索到其周围的局部信息。

也就是说，如果用如果 GCN 具有具有固定层数，并不能让为所有节点带来最佳的向量表示。

2.JKnet

通过上面的分析，作者得出结论：目前通用的聚合方法引起的固定但与结构相关的影响半径大小并不能实现所有节点和人物的最佳向量表示。较大的半径可能会导致 over-smooth，而较小的半径可能会导致不稳定和信息聚集不足的问题。

为此，作者提出了两个简单而又强大的架构：跳跃连接（jump connection）和自适应选择性聚集机制。

下图阐述了作者的想法：

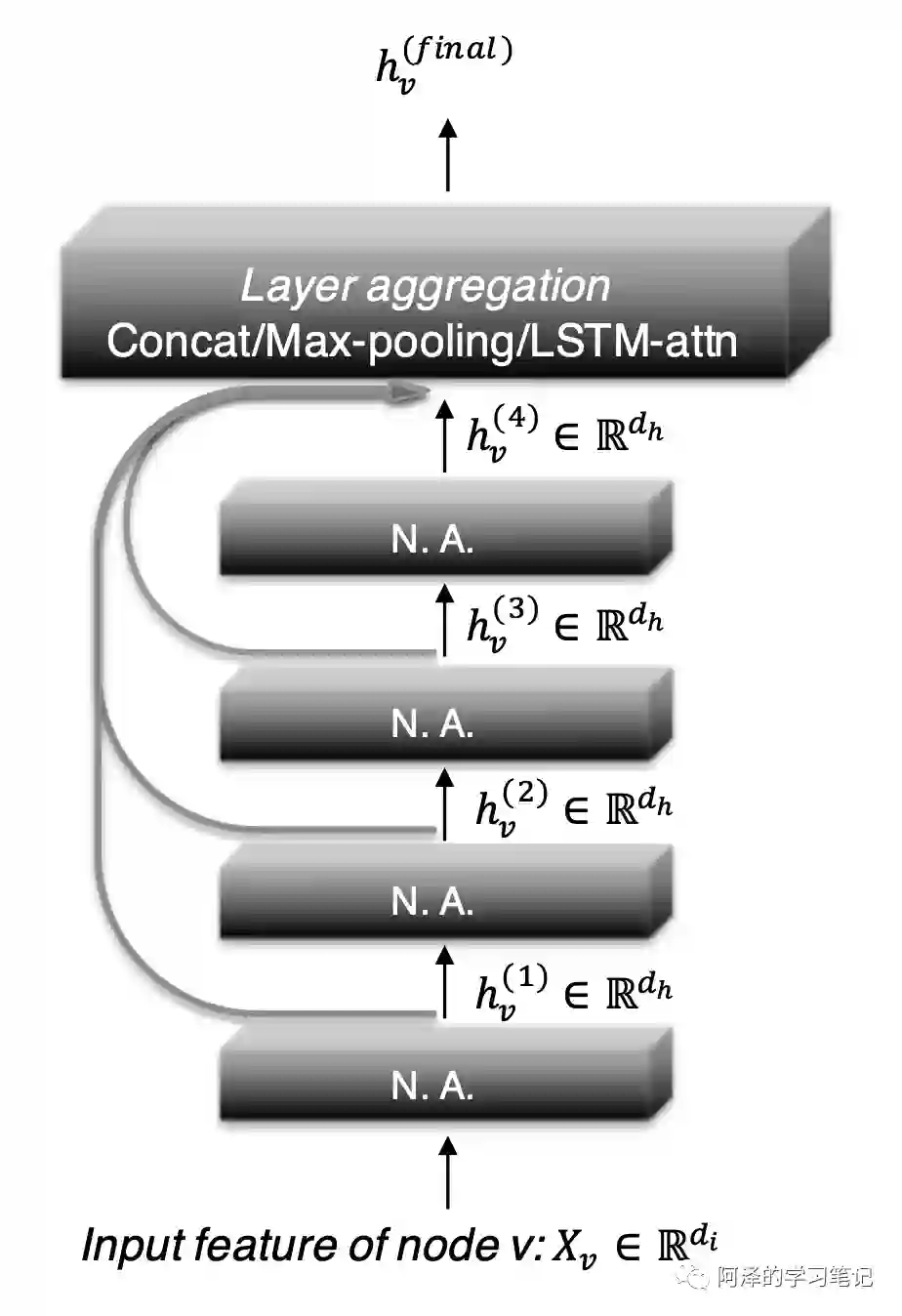
和普通的 GCN 一样，每一层都会聚合来自上一层的领域来增加节点的影响大小。但在最后一层中，每个节点都会从之前的中间表示中筛选一些进行合并。这一步是针对每个节点独立完成的，所以模型可以根据需要为每个节点调整有效的领域大小，从而完成自适应选择性聚集。

作者给出了三种融合方法：

Concatenation：直接将各层的表达串联合，送入到 Linear 层进行分类。这种方法不支持节点的自适应选择，而是找到最适合整个数据集的方式来组合子图特征。这种方法适用于较规则的小型图，并且一定概率上通过（Linear 层的）权重共享来减少过拟合；
Max-pooling：为每个节点进行基于 element-wise 的 max-pooling 操作。这样的操作可以让节点选择从底层学习局部领域的信息，而是去从高层学习全局领域的信息。max-pooling 是自适应的，其优点在于不会引入额外的参数；
LSTM-attention：Attention 机制是一个有效的可以学习节点信息的方式。每一个节点都会算出一个基于层的 attention 分数，其表示对于节点来说，不同层的重要性，然后基于此进行加权求和。LSTM-attention 是将各层的表达送入到双向的 LSTM 中，这样每个层都会有一个前向表达和后向表达，然后将这个表达串联拼接送入到 Linear 层来拟合出一个 score，对每一层的 score 进行归一化后边得到 attention score：，最后加权求和得到最终的表达。

这种设计的关键思想在于：在查看所有层的学习特征之后，不同位置的节点可以确定其子图特征的重要性，而不是为所有节点固定相同的权重。

下图展示了利用 Max-pooling 聚合的 6 层 JK-Net，不同子图结构的可视化展示：

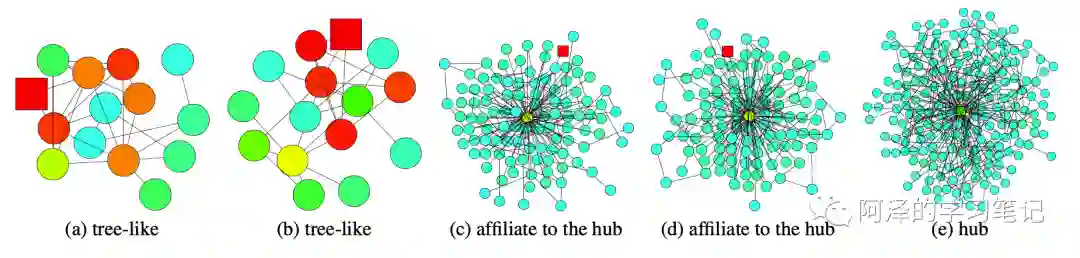
a 和 b 为边缘节点，其影响的节点停留在小社区中；而和中心节点有关（c，d）的节点或者中心节点（e），其影响分散在一个合理范围内的相邻节点上。

3.Experiments

简单看一下实验。

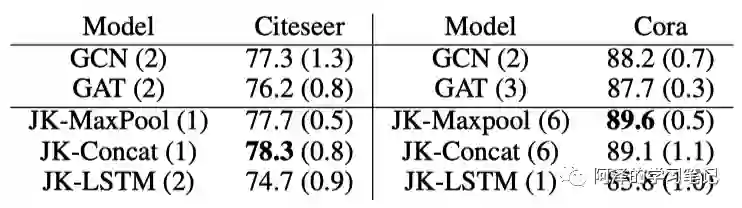
下图为不同模型在不同数据集中的表现，其中 JK-Net 基于 GCN 模型。LSTM 效果不好主要是因为数据集太小了：

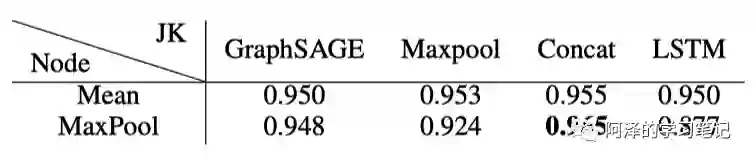
下图为基于 GraphSAGE 的 JK-Net 在 Reddit 数据集中的表现，层数皆为 2 层，评价指标为 F1：

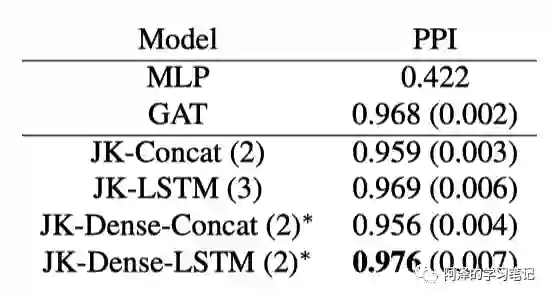
下图为在 PPI 数据集中表现，LSTM 的效果就显示出来了

4.Conclusion

总结：本篇论文分析了 GCN 随着层数增大而导致性能下降的原因，并受分析结果启发提出了一个网络架构——JK-Net。JK-Net 通过自适应学习处在不同位置的节点聚合不同领域，从而可以改善节点的表示形式。JK-Net 可与现有的模型架构相结合，并在多个数据集中取得了 SOTA 的成绩。

5.Reference

《Representation Learning on Graphs with Jumping Knowledge Networks》

推荐阅读

征稿启示| 200元稿费+5000DBC（价值20个小时GPU算力）

文本自动摘要任务的“不完全”心得总结番外篇——submodular函数优化

Node2Vec 论文+代码笔记

模型压缩实践收尾篇——模型蒸馏以及其他一些技巧实践小结

中文命名实体识别工具（NER）哪家强？

学自然语言处理，其实更应该学好英语

斯坦福大学NLP组Python深度学习自然语言处理工具Stanza试用

太赞了！Springer面向公众开放电子书籍，附65本数学、编程、机器学习、深度学习、数据挖掘、数据科学等书籍链接及打包下载

数学之美中盛赞的 Michael Collins 教授，他的NLP课程要不要收藏？

自动作诗机&藏头诗生成器：五言、七言、绝句、律诗全了

模型压缩实践系列之——bert-of-theseus，一个非常亲民的bert压缩方法

这门斯坦福大学自然语言处理经典入门课，我放到B站了

关于AINLP

AINLP 是一个有趣有AI的自然语言处理社区，专注于 AI、NLP、机器学习、深度学习、推荐算法等相关技术的分享，主题包括文本摘要、智能问答、聊天机器人、机器翻译、自动生成、知识图谱、预训练模型、推荐系统、计算广告、招聘信息、求职经验分享等，欢迎关注！加技术交流群请添加AINLPer(id：ainlper)，备注工作/研究方向+加群目的。