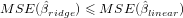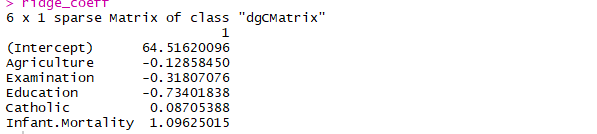数据分析师应该知道的16种回归技术:岭回归
岭回归可以看成是最小二乘回归的一种补充,通过牺牲最小二乘的无偏性换取数值的稳定性。学习岭回归之前了解下正则化是很有必要的。
在线性回归中,有时模型可以很好拟合训练集而不能有效反映测试集的特征,称这种现象为过拟合。对过拟合问题,可通过正则化解决,它在目标函数中添加惩罚项,利用惩罚项控制模型复杂度。
一般来说,数据出现下列情形,考虑使用正则化方法
变量非常多
样本数远小于变量数
较高的多重共线性
惩罚项是在目标函数中添加的对回归系数的约束项。根据惩罚项的不同,正则化分为L1正则化和L2正则化。L1正则化添加的惩罚项为系数的绝对值之和,L2正则化添加的惩罚项为系数平方和,它们分别对应岭回归和Lasso回归。另外还有一种介于L1和L2正则化之间的方法,称为弹性网络回归。本文主要讲岭回归,后续会分享Lasso和弹性网络回归的内容。
线性回归通过最小化误差平方和获得回归系数的估计值,岭回归是通过添加L2损失函数(系数平方和)对回归系数进行限制,此时的目标函数为:
上式的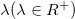
解目标函数,得到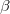
同线性回归相比,岭回归的优势:
不管
是否正定,总存在
使得
正定,即对任意数据集,岭回归总存在唯一解
总存在
使
最后一个问题是正则参数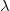
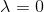
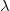
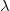
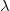
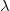
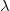
案例
下面考虑datasets包中的swiss数据集,该数据集描述瑞士47个法语地区的生育率和5个社会指标之间的关系。
R中的glmnet包提供了进行岭回归的函数cv.glmnet,函数中的参数alpha=0(默认)对应岭回归,alpha=1对应lasso回归,alpha在0,1之间对应松弛网络回归。另一个有用逻辑参数keep(默认FALSE)控制是否保存每个lambda下回归系数的估计值。
利用岭回归拟合swiss数据集
X <- swiss[,-1]
y <- swiss[,1]
library(glmnet)
model <- cv.glmnet(as.matrix(X),y,alpha = 0,keep=T,
lambda = 10^seq(4,-1,-0.1))
best_lambda <- model$lambda.min
ridge_coeff <- predict(model,s = best_lambda,
type = "coefficients")
ridge_coeff
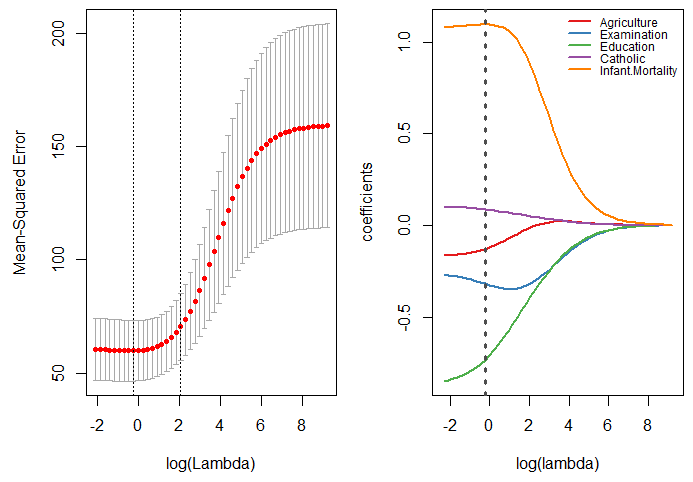
绘制不同lambda下回归系数及模型MSE,图中灰色虚线对应最优lambda值。
op=par(mfrow=c(1,2))
plot(model)
hatbeta <- as.matrix(model$glmnet.fit$beta)
loglambda = log(10^seq(4,-1,-0.1))
plot(1,type = 'n',xlim = c(-2.4,9.3),ylim = c(-0.85,1.1),
xlab = 'log(lambda)',ylab = 'coefficients')
colrs = RColorBrewer::brewer.pal(5,"Set1")
for (i in 1:5) {
lines(loglambda,hatbeta[i,],col=colrs[i],lwd=2)
}
abline(v=log(best_lambda),lty=3,lwd=3,col='gray30')
legend('topright',rownames(hatbeta),lty = 1,lwd=2,
col=colrs,bty = 'n',cex = 0.75)
par(op)
推荐阅读
从零开始深度学习第6讲:神经网络优化算法之从SGD到Adam
谈谈大数据的那点事(5) ——《新媒体将会成为大数据研究的重要领域》

长按二维码关注“数萃大数据”
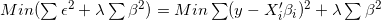
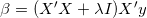
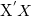 是否正定,总存在
是否正定,总存在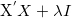 正定,即对任意数据集,岭回归总存在唯一解
正定,即对任意数据集,岭回归总存在唯一解