开发 | 为什么ResNet和DenseNet可以这么深?一文详解残差块为何有助于解决梯度弥散问题。
AI科技评论按:本文作者Professor ho,原文载于其知乎主页,雷锋网获其授权发布。
传统的“提拉米苏”式卷积神经网络模型,都以层叠卷积层的方式提高网络深度,从而提高识别精度。但层叠过多的卷积层会出现一个问题,就是梯度弥散(Vanishing),backprop无法有效地把梯度更新到前面的网络层,导致前面的层参数无法更新。
而BatchNormalization(BN)、ResNet的skip connection就是为了解决这个问题,BN通过规范化输入数据改变数据分布,在前传过程中消除梯度弥散。而skip connection则能在后传过程中更好地把梯度传到更浅的层次中。那么问题来了,
为什么加了一个捷径就能把梯度传到浅层网络?
这个要从神经网络梯度更新的过程说起,如果读者已经非常熟悉神经网络的梯度更新,可以快进这部分,但这个梯度更新的原理才是整个问题的关键。
神经网络梯度更新过程的简单回顾
这里主要引用cs231n的讲义,个人认为这是理解神经网络梯度更新讲得最好的课程,建议直接看cs231n 2016的视频讲解,Andrej Karpathy在视频里讲得非常清晰,配合他的PPT看非常易懂,这里是地址:CS231n Winter 2016: Lecture 4: Backpropagation, Neural Networks 1。这里是YouTube视频链接,国内的朋友请百度:cs231n 2016视频。
由于篇幅原因,就不像Andrej在视频里从实例讲起那么详细了,这里就只讲梯度在中间层传播时的计算过程,如果还没完全了解神经网络梯度更新原理的,建议先把视频看完。
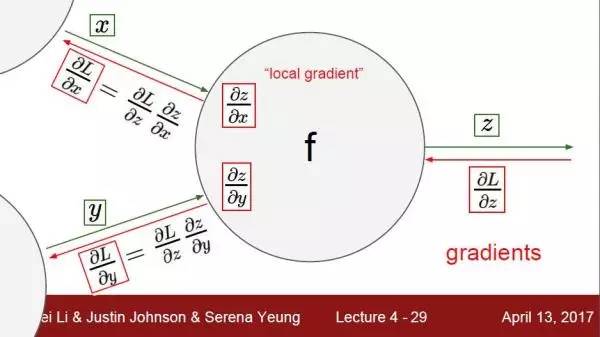
图1 来自斯坦福cs231n课程slides
当梯度传播到中间层的神经元f时,如图1所示,来自上一层的梯度dLdz从右边z进入,传到中间的神经元。此神经元在左边有两个输入,分别是x和y,为了计算L对于x和y的梯度dLdx和dLdy,就必须先计算dzdx和dzdy,根据复合函数求导公式,dLdx = dLdz * dzdx,dLdy = dLdz * dzdy,这样就能算出传播到x和y的梯度了。也就是说通过这个方法,来自深一层的梯度就能传播到x和y当中。
图2
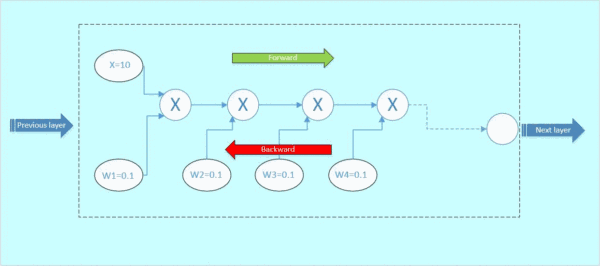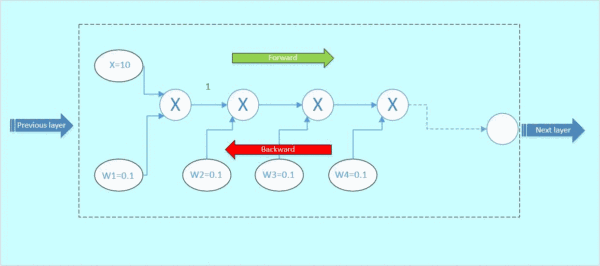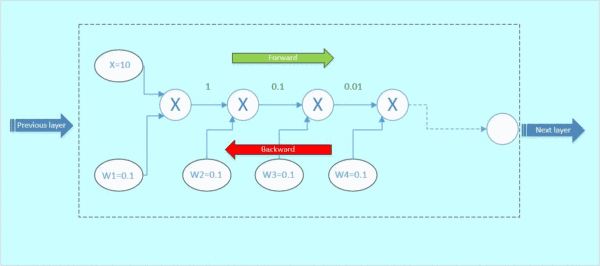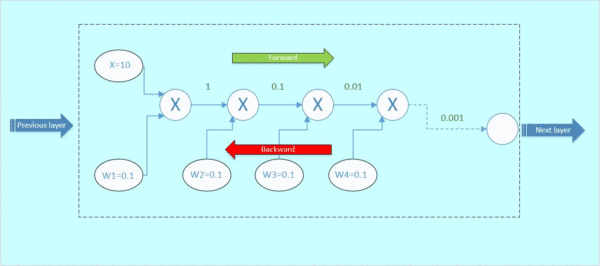
让我们来考虑一个新的情况。图2虚线框为一个神经元block,假设输入x为10,权重w1=0.1,w2=0.1,w3=0.1,w4=0.1,每个神经元对输入的操作均为相乘。我们对它进行前传和后传的计算,看看梯度的变化情况:
前向传播:
首先x与w1相乘,得到1;1与w2相乘,得到0.1,以此类推,如下面的gif图绿色数字表示
图3 前向传播
后向传播:
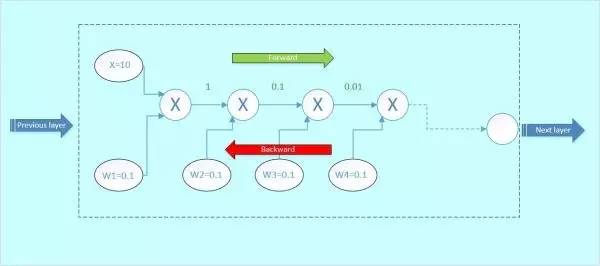
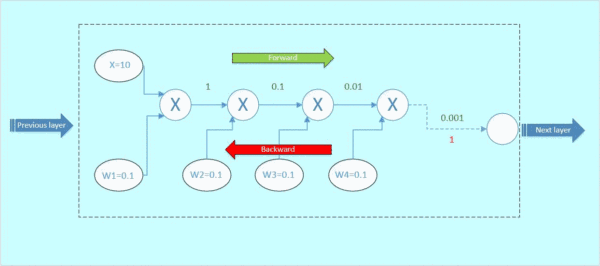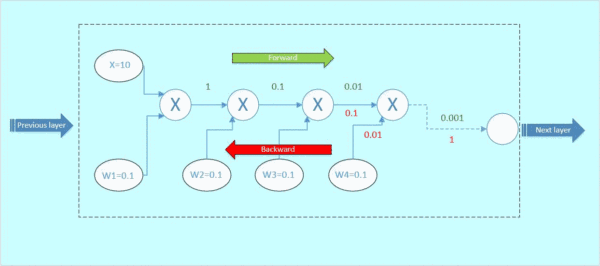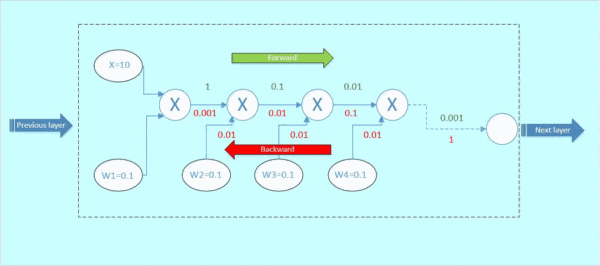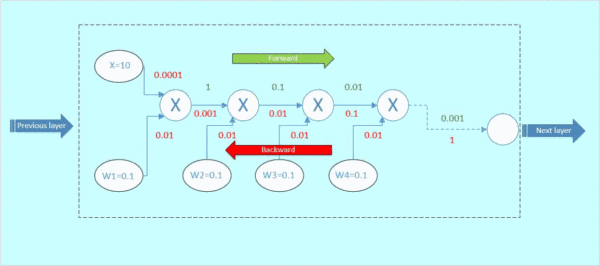
假设从下一层网络传回来的梯度为1(最右边的数字),后向传播的梯度数值如下面gif图红色数字表示:
图4 后向传播
那么这里可以看到,本来从上一层传过来的梯度为1,经过这个block之后,得到的梯度已经变成了0.0001和0.01,也就是说,梯度流过一个blcok之后,就已经下降了几个量级,传到前一层的梯度将会变得很小!
这就是梯度弥散。假如模型的层数越深,这种梯度弥散的情况就更加严重,导致浅层部分的网络权重参数得不到很好的训练,这就是为什么在Resnet出现之前,CNN网络都不超过二十几层的原因。
防止梯度弥散的办法
既然梯度经过一层层的卷积层会逐渐衰减,我们来考虑一个新的结构,如图5:
图5
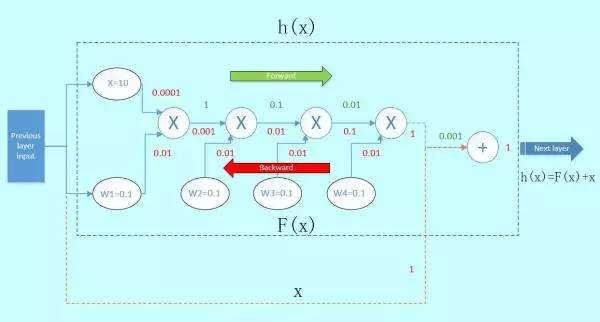
假如,我们在这个block的旁边加了一条“捷径”(如图5橙色箭头),也就是常说的“skip connection”。假设左边的上一层输入为x,虚线框的输出为f(x),上下两条路线输出的激活值相加为h(x),即h(x) = F(x) + x,得出的h(x)再输入到下一层。
图6
当进行后向传播时,右边来自深层网络传回来的梯度为1,经过一个加法门,橙色方向的梯度为dh(x)/dF(x)=1,蓝色方向的梯度也为1。这样,经过梯度传播后,现在传到前一层的梯度就变成了[1, 0.0001, 0.01],多了一个“1”!正是由于多了这条捷径,来自深层的梯度能直接畅通无阻地通过,去到上一层,使得浅层的网络层参数等到有效的训练!
这个想法是何等的简约而伟大,不得不佩服作者的强大的思维能力!
直观理解
图7
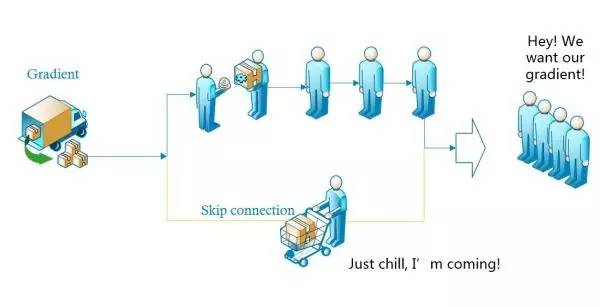
如图7,左边来了一辆装满了“梯度”商品的货车,来领商品的客人一般都要排队一个个拿才可以,如果排队的人太多,后面的人就没有了。于是这时候派了一个人走了“快捷通道”,到货车上领了一部分“梯度”,直接送给后面的人,这样后面排队的客人就能拿到更多的“梯度”。
Resnet与DenseNet
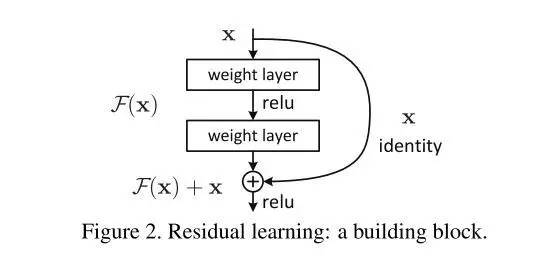
图8
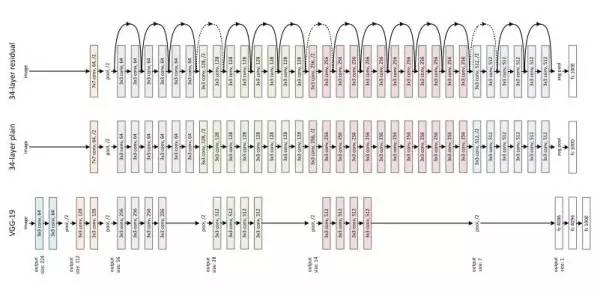
ResNet正是有了这样的Skip Connection,梯度能畅通无阻地通过各个Res blocks,作者何凯明说到,唯一影响深度的就是内存不足,因此只要内存足够,上千层的残差网络也都能实现。
而DenseNet更为极端,它的skip connection不仅仅只连接上下层,直接实现了跨层连接,每一层获得的梯度都是来自前面几层的梯度加成。
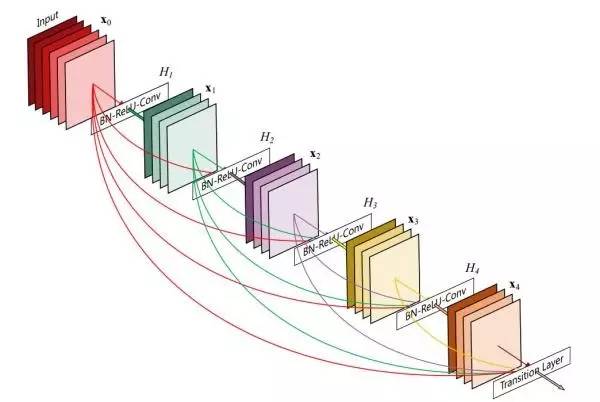
图9 DenseNet结构
DenseNet在增加深度的同时,加宽每一个DenseBlock的网络宽度,能够增加网络识别特征的能力,而且由于DenseBlock的横向结构类似 Inception block的结构,使得需要计算的参数量大大降低。因而此论文获得了CVPR2017最佳论文奖项!
图10 DenseNet详细结构 来自原论文
总结
ResBlock与BN的结合能够完美解决梯度弥散的问题,这使得更深的网络成为可能。卷积神经网络除了不断往深度发展,在宽度上也不断拓展,两者结合起来可以创造出更强大的CNN模型。期待更多杰出的工作!
由于笔者水平尚浅,对上面的概念理解或许有偏差,欢迎各位指正,不胜感激。如果觉得这篇文章对您有帮助,请分享给您的朋友,让更多人一起学习。
————— 给爱学习的你的福利 —————
CCF-ADL81:从脑机接口到脑机融合
顶级学术阵容,50+学术大牛
入门类脑计算知识,了解类脑智能前沿资讯
课程链接:http://www.mooc.ai/course/114
或点击文末阅读原文
————————————————————