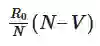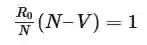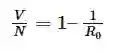数学原理如何帮助人类对抗流感

2018 年 3 月 6 日 中科院物理所 Patrick Honner

科学无国界

我们是知识的搬运工

福利时间

今天我们将送出三套由中国科学技术大学出版社提供的数学与艺术启蒙系列丛书《有魔法的形状》。

想和宝贝一起踏上寻找魔法王国的探险旅途吗？想陪伴宝贝在边阅读边动手的快乐体验中认识颜色、熟悉形状、创意拼塔、体验计数、感知这个世界的美好吗？你听，机器人弗兰奇、恐龙雷克斯、小怪兽布鲁和小丑巴比正在呼唤宝贝们的帮助呢！赶紧让这套精美的丛书成为孩子成长路上的好伙伴吧！

数学启蒙，认识几何形状；艺术启蒙，感知丰富的颜色和图案；故事探险，穿越洞洞设计的魔法门、天空之洞；亲子创意拼搭，激发儿童想象力和创造力。

如何才能得到这套《有魔法的形状》系列丛书呢？参与的方式非常简单！只要你认真阅读下面的这篇文章，思考文末提出的问题，严格按照［互动：你的答案］的格式在评论区留言，就有机会获得奖品！（PS：格式不符合要求者无效）截止到本周四中午12点，点赞数前三名的朋友将获得一套《《有魔法的形状》系列丛书。

【互动问答示例】

互动：这里就可以自由发挥你的答案啦~

作者：Patrick Honner

翻译：螳吉呵呵

审校：山寺小沙弥

让我们假设你听到了一个谣言但你忍不住想讲给其他人听。因为你非常痛恨造谣者所以你仅仅把这个谣言告诉了一个人就不再提起它。看起来没什么大不了的，对吧？毕竟，如果听到谣言的人和你一样只把它告诉一个人，这则谣言不会传播的特别快。如果每天新增加一个人听到谣言，30天后谣言只会传播到包括你在内的31个人耳朵里。

如果每个人把谣言告诉两个人情况会是什么样子？事实上，情况非常糟糕。如果头一天听到谣言的人在一天内把它传递给另外两个人，30天后将有超过全球人口四分之一的人会听到这则谣言（准确的说是2147483647个人）。为什么告诉一个人还是告诉两个人这么微小的区别会对结果造成如此大的影响？答案是增长速率的改变。

在第一个例子中，每天新增同样多的人听到谣言。不管是今天，明天，后天还是将来，这意味着每天新增的人数相同。在我们的例子里，每天新增一个人。

但如果每天新增加的人数是前一天的两倍，新增人数就会指数增长：第一天有两个人听到谣言，第二天四个人听到谣言，第三天八个人听到谣言，以此类推。到第三十天，将新增2^30人听到谣言。（一些不理想的情况后面会提到）

两个例子的差别为什么如此之大？这就是线性函数和指数函数的差别。线性函数被一个恒定的增长率所描述，就像每天新增一个人听到谣言。线性增长稳定且缓慢，相同的时间增加相同的数量。和线性增长不同，指数增长的速率也在不断增加--每天新增人数也在持续增长。第一天新增2人，第二天新增4人，第三天新增8人等。

这就是30天后31人和20亿人听到谣言的区别所在。仅仅因为每个人把谣言传递给一个人还是两个人就造成如此大的区别。

图解表示每天知道谣言的人数。横轴代表时间，纵轴代表人数。绿线表示线性增长，几乎平行于横轴。蓝线表示指数增长，很快突破20亿。

这个基础的数学模型包含了某类特定的繁殖模式的本质，它不仅仅可以用来描述谣言的传播。

像所有的基础模型一样，它忽略和简化了很多复杂的因素，比如传播的可能性和总人口的规模，但它是研究谣言如何传播、人口如何增长以及疾病如何传播的一个很好的出发点。

传染病的传播方式和谣言相同：某个人得病并把它传播给其他的人。当然，也有不同的地方，不过这个基础模型在两种情形中都可以适用。在我们关于谣言的简单的模型中，我们看到传播速度上的微小区别如何造成最终听到谣言的人数的巨大差别。这种差别在疾病传播的情形中仍然存在。

每一种传染病在社会中的传播速度都依赖于生物的、环境的和社会的因素。流行病学家尝试把这些因素归纳进传染病的“基础传播数”中。这是每个患者可能传染的人数的平均值，我们把它记为R0。在我们之前关于谣言的例子中，基础传播数是R0=1和R0=2；“传染周期”是一天。

一些常见疾病的基础传播数

疾病	R0
麻疹	12-18
天花	5-7
流行性腮腺炎	4-7
流行性感冒（1918病毒株）	2-3

来源: CDC and NIH

不难发现，这些疾病的基础传播数都大于1 。它们如此危险的部分原因是：每个患者平均可以感染超过一个人，所以新增患者的个数将指数式增长。这在全体人类中会造成毁灭性的传染。我们是否能够将指数式增长变成线性增长，也就是说将R0降低为1？

想要实现这个目标就需要疫苗的帮助。当一个人接种了疫苗，他就可以抵抗疾病的感染：尽管接种成功率会有变化，但是出于简单考虑我们假设成功率是百分之百，也就是说接种疫苗就代表你获得了对某种疾病的抵抗力。疫苗不但可以直接保护接种疫苗的人也可以间接保护更广泛的人群。如果社会中很多人都接种了疫苗，疾病的传播就不会非常迅速。

实际上，广泛接种疫苗可以降低疾病的有效传播数（effective reproduction number）。如果足够多的人接种了疫苗，甚至可以把有效传播数降低到1，这样就能实现疾病按照线性速度传播。所以，如果想把有效传播数降低至1需要多少人接种疫苗？

让我们考虑基础传播数可以告诉我们什么信息。考虑一种R0 =2的流感。这意味着一个患者将平均传染给两个人。R0 =2提供我们很多信息：这个疾病有多容易传播，感染的周期以及一个患者在一个给定的感染周期内将传染多少个人。通过研究这个数字，我们很容易发现疫苗怎么把它减小。

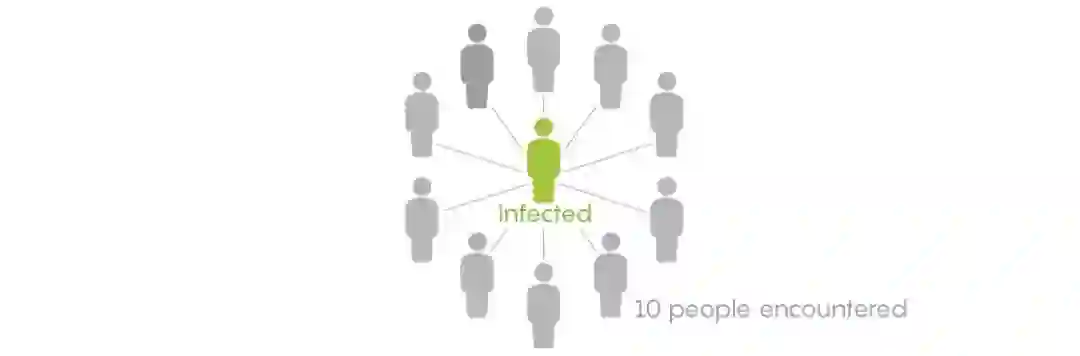
假设一个感染了R0 =2的流感的患者在患病期间会接触到10个人。我们将它画成图解，我们用中间绿色的小人代表患者并用箭头指向10个接触到的人。

每个和患者有接触的人都有可能感染流感，但是R0=0意味着接触到的10个人中平均会有2个人被感染。

一般而言，我们可以说每个人有20%的概率被感染。

如果10个人中有两人接种了流感疫苗。为了简单起见我们仍然假定接种疫苗意味着对疾病的完全免疫，也就是说不会在受到感染。但是剩下的8个人仍然会有20%被感染的概率。这意味着，平均来讲1.6个人会被感染。

所以如果10个人中有两个人接种了疫苗，一个患者平均上讲只能感染1.6个然。疫苗有效地把基础传播数从2降低为1.6。接下来的问题是我们怎样才能把基础传播数降低为1来对抗指数式增长？

我们再次假设一个患者在一个感染周期内会接触10个人，并且每个未接种疫苗的人有20%被感染的几率。假设10个人中有V个人接种了疫苗。我们可以预见，平均上讲，剩下的10-V个为接种的人中有20%会感染疾病。为了实现线性增长而不是指数型增长，我们需要新的被感染数降低为1 。事实上我们要求公式0.2 × (10 − V) = 1 成立。

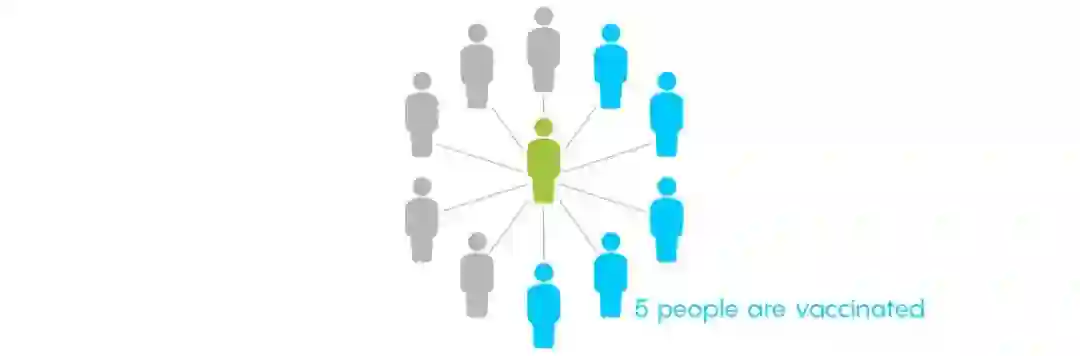
简单的代数计算告诉我们方程的解是V=5。让我们看一下10个人中有5人接种疫苗时发生了什么。我们在图解中用蓝色小人代表接种疫苗的人。

疫苗实际上将5个蓝色小人移出了图解，因为疾病对他们没有影响。

剩下的5个人每个人被感染的概率仍然是20%，所以他们之中平均会有一个人被感染。这意味着，原本的10个人中会有一个人被感染：结果就是如果10个人里有5个人接种疫苗，我们就可以把疾病的R0降低为1。

这个过程可以被推广到任何基础传播数R0。如果我们假设每个患者在一个传染周期内接触N个人，我们可以预见到，这些人中平均有R0/N的概率会患病。但是如果V是N个人中接种疫苗的人数，那么：

就代表新的感染人数。我们想让它变成1，所以需要：

解出V/N的值是有意义的，因为V是N个人中被接种的人数，V/N代表了总数中需要被接种的百分比。数学运算告诉我们：

这意味着如果总人口中接种疫苗的人数达到1 − 1/R0 ，一个患者平均只能新感染一个人。事实上，1 − 1/R0 决定了疾病的增长速度是指数式的还是线性的。

当人群中有1 − 1/R0 比例的人接种了疫苗，这个群体就获得了一种整体的免疫力：不是一个个体抵御疾病的能力，而是人群抵御疾病在人群中按照指数式传播的免疫力。这个性质被称为“群体免疫（herd immunity）”。一个群体像要达到群体免疫所需要的接种疫苗的比例被称为“群体免疫门槛（herd immunity threshold（HIT））”。下表展示了几种疾病HIT的例子：

疾病	R0	1-1/ R0	HIT
麻疹	12	1-1/12	91.7%
天花	5	1-1/5	80%
流行性腮腺炎	4	1-1/4	75%
流行性感冒	2	1-1/2	50%

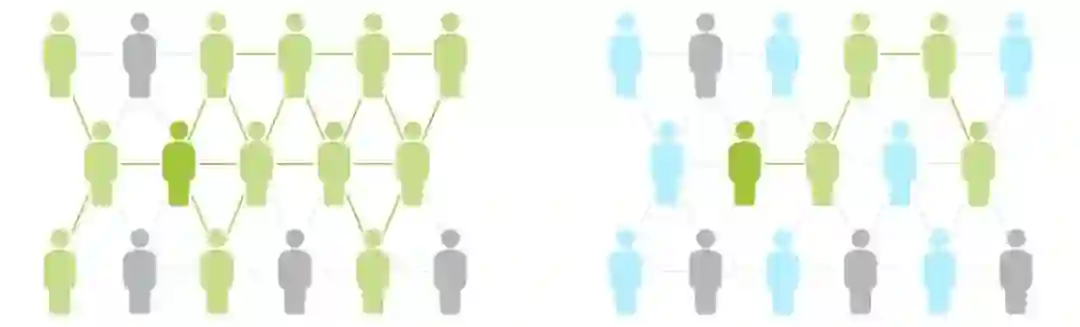
我们已经清楚地看到，接种某种疫苗并不仅仅为个体提供了保护，同时也保护了整个群体。当接种比例达到了HIT，疾病在人群中散播的速度就可以低至不至于发生大的灾难。普遍的疫苗接种将左图的传播模式转变成右图那样，左图中有很多潜在的传播路径，而右图中的传播路径就少很多，这大大减少了疾病爆发式传播的可能性。

群体免疫的一个重要的特征是它甚至可以保护没有接种疫苗的个体。因为疾病更不容易广泛传播，每个人面临的风险都降低了，包括没有接种疫苗的人。这对不适合接种疫苗的人，比如婴儿、老人和身体虚弱的人是非常重要的。尽管我们假设了疫苗百分之百有效，在有效率不是百分之百时群体免疫依然可以实现：普遍的疫苗接种仍然会降低每个患者平均可以感染的人数，因此可以降低疾病的有效传播数。

我们已经看到线性增长和指数增长之间巨大的区别。当它在疾病传播中体现时，它将关系到生死。数学揭示了疫苗和群体免疫的重要性，请告诉你的一个朋友。更好的是，告诉两个朋友。

原文链接：

https://www.quantamagazine.org/flu-vaccines-and-the-math-of-herd-immunity-20180205/

互动问题

【互动问题：学不好数学是怎样一种体验?】

请大家严格按照互动：问题答案的格式在评论区留言参与互动，格式不符合要求者无效。

截止到本周四中午12点，点赞数前三名的朋友将获得我们送出的图书一套。

特别说明：一套书籍一共有4本书哦~

编辑：山寺小沙弥

近期热门文章Top10

↓ 点击标题即可查看 ↓

1. 物理定律告诉你，天下有情人终将分手！