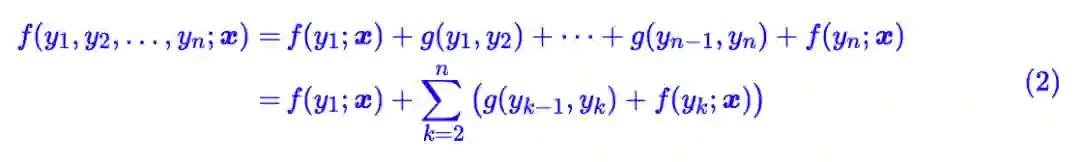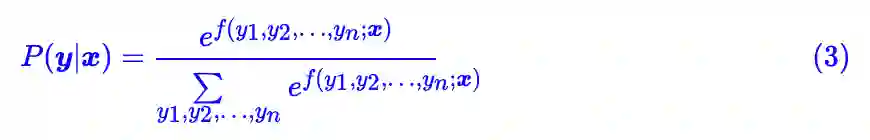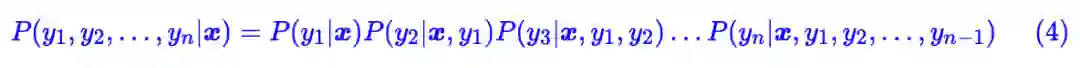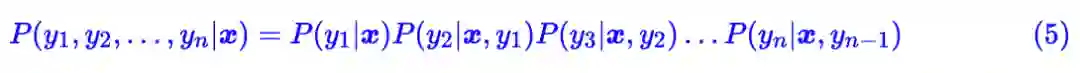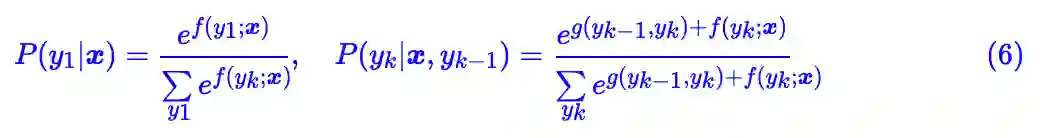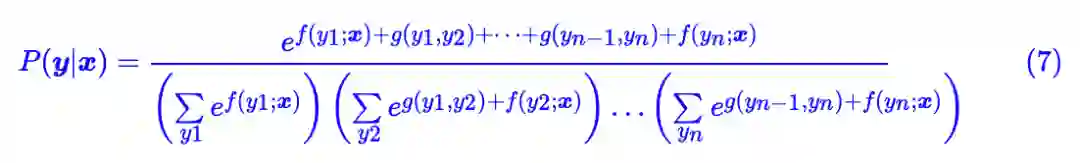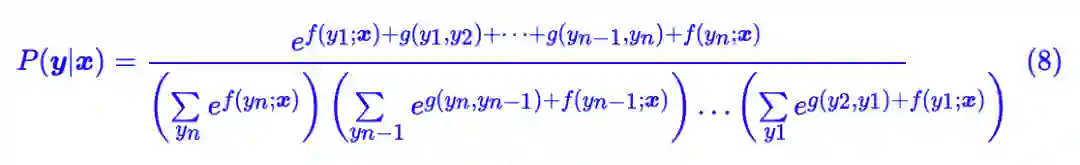CRF用过了，不妨再了解下更快的MEMM？

©PaperWeekly 原创 · 作者｜苏剑林

单位｜追一科技

研究方向｜NLP、神经网络

HMM、MEMM、CRF 被称为是三大经典概率图模型，在深度学习之前的机器学习时代，它们被广泛用于各种序列标注相关的任务中。一个有趣的现象是，到了深度学习时代，HMM 和 MEMM 似乎都“没落”了，舞台上就只留下 CRF。

相信做 NLP 的读者朋友们就算没亲自做过也会听说过 BiLSTM+CRF 做中文分词、命名实体识别等任务，却几乎没有听说过 BiLSTM+HMM、BiLSTM+MEMM 的，这是为什么呢？

今天就让我们来学习一番 MEMM，并且通过与 CRF 的对比，来让我们更深刻地理解概率图模型的思想与设计。

模型推导

从 MEMM 全称 Maximum Entropy Markov Model，中文名可译为“最大熵马尔可夫模型”。不得不说，这个名字可能会吓退 80% 的初学者：最大熵还没搞懂，马尔可夫也不认识，这两个合起来怕不是天书？而事实上，不管是 MEMM 还是 CRF，它们的模型都远比它们的名字来得简单，它们的概念和设计都非常朴素自然，并不难理解。 

回顾 CRF

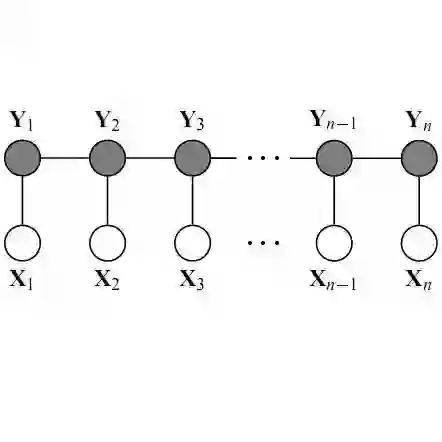
作为对比，我们还是来回顾一下 CRF。说是“回顾”，是因为笔者之前已经撰文介绍过 CRF 了，如果对 CRF 还不是很了解的读者，可以先去阅读旧作简明条件随机场CRF介绍 | 附带纯Keras实现。简单起见，本文介绍的 CRF 和 MEMM 都是最简单的“线性链”版本。

本文都是以序列标注为例，即输入序列 x=(x1,x2,…,xn)，希望输出同样长度的标签序列 y=(y1,y2,…,yn)，那么建模的就是概率分布：

CRF 把 y 看成一个整体，算一个总得分，计算公式如下：

这个打分函数的特点就是显式地考虑了相邻标签的关联，其实 g(yk−1,yk) 被称为转移矩阵。现在得分算出来了，概率就是得分的 softmax，所以最终概率分布的形式设为：

如果仅局限于概念的话，那么 CRF 的介绍到此就结束了。总的来说，就是将目标序列当成一个整体，先给目标设计一个打分函数，然后对打分函数进行整体的 softmax，这个建模理念跟普通的分类问题是一致的。CRF 的困难之处在于代码实现，因为上式的分母项包含了所有路径的求和，这并不是一件容易的事情，但在概念理解上，笔者相信并没有什么特别困难之处。

更朴素的 MEMM

现在我们来介绍 MEMM，它可以看成一个极度简化的 seq2seq 模型。对于目标 (1) ，它考虑分解：

然后假设标签的依赖只发生在相邻位置，所以：

接着仿照线性链 CRF 的设计，我们可以设：

至此，这就得到了 MEMM 了。由于 MEMM 已经将整体的概率分布分解为逐步的分布之积了，所以算 loss 只需要把每一步的交叉熵求和。

两者的关系

将式 (6) 代回式 (5) ，我们可以得到：

对比式 (7) 和式 (3)，我们可以发现，MEMM 跟 CRF 的区别仅在于分母（也就是归一化因子）的计算方式不同，CRF 的式 (3) 我们称之为是全局归一化的，而 MEMM 的式 (7) 我们称之为是局部归一化的。

模型分析

这一节我们来分析 MEMM 的优劣、改进与效果。 

MEMM 的优劣

MEMM 的一个明显的特点是实现简单、速度快，因为它只需要每一步单独执行 softmax，所以 MEMM 是完全可以并行的，速度跟直接逐步 Softmax 基本一样。

而对于 CRF，式 (3) 的分母并不是那么容易算的，它最终转化为一个递归计算，可以在 O(n) 的时间内算出来（具体细节还请参考简明条件随机场CRF介绍 | 附带纯Keras实现），递归就意味着是串行的，因此当我们模型的主体部分是高度可并行的架构（比如纯 CNN 或纯 Attention 架构）时，CRF 会严重拖慢模型的训练速度。后面我们有比较 MEMM 和 CRF 的训练速度（当然，仅仅是训练慢了，预测阶段 MEMM 和 CRF 的速度都一样）。 

至于劣势，自然也是有的。前面我们提到过，MEMM 可以看成是一个极度简化的 seq2seq 模型。既然是这样，那么普通 seq2seq 模型有的弊端它都有。seq2seq 中有一个明显的问题是 exposure bias，对应到 MEMM 中，它被称之为 label bias，大概意思是：在训练 MEMM 的时候，对于当前步的预测，都是假设前一步的真实标签已知。

这样一来，如果某个标签 A 后面只能接标签 B ，那么模型只需要通过优化转移矩阵就可以实现这一点，而不需要优化输入 x 对 B 的影响（即没有优化好 f(B;x)）；然而，在预测阶段，真实标签是不知道的，我们可能无法以较高的置信度预测前一步的标签 A ，而由于在训练阶段，当前步的 f(B;x) 也没有得到强化，所以当前步 B 也无法准确预测，这就有可能导致错误的预测结果。 

双向 MEMM

label bias可能不好理解，但我们可以从另外一个视角看 MEMM 的不足：事实上，相比 CRF，MEMM 明显的一个不够漂亮的地方就是它的不对称性——它是从左往右进行概率分解的。

笔者的实验表明，如果能解决这个不对称性，能够稍微提高 MEMM 的效果。笔者的思路是：将 MEMM 也从右往左做一遍，这时候对应的概率分布是：

然后也算一个交叉熵，跟从左往右的式 (7) 的交叉熵平均，作为最终的 loss。这样一来，模型同时考虑了从左往右和从右往左两个方向，并且也不用增加参数，弥补了不对称性的缺陷。作为区分，笔者类比 Bi-LSTM 的命名，将其称为 Bi-MEMM。 

注：Bi-MEMM 这个名词并不是在此处首次出现，据笔者所查，首次提出 Bi-MEMM 这个概念的，是论文 Bidirectional Inference with the Easiest-First Strategy for Tagging Sequence Data [1]，里边的 Bi-MEMM 是指一种 MEMM 的双向解码策略，跟本文的 Bi-MEMM 含义并不相同。

实验结果演示

为了验证和比较 MEMM 的效果，笔者将 CRF 和 MEMM 同时写进了 bert4keras [2] 中，并且写了中文分词 [3] 和中文命名实体识别 [4] 两个脚本。在这两个脚本中，从 CRF 切换到 MEMM 非常简单，只需将 ConditionalRandomField 替换为 MaximumEntropyMarkovModel 。 

详细的实验数据就不贴出来了，反正就是一些数字罢了，下面直接给出一些相对比较的结果： 

1. 相同的实验参数下，Bi-MEMM 总是优于 MEMM，MEMM 总是优于 Softmax； 

2. 相同的实验参数下，CRF 基本上不差于 Bi-MEMM； 

3. 当编码模型能力比较强时，CRF 与 Bi-MEMM 效果持平；当编码模型较弱时，CRF 优于 Bi-MEMM，幅度约为 0.5% 左右； 

4. 用 12 层 bert base 模型作为编码模型时，Bi-MEMM 比 CRF 快 25%；用 2 层 bert base 模型作为编码模型时，Bi-MEMM 比 CRF 快 1.5 倍。

注：由于笔者发现 Bi-MEMM 效果总比 MEMM 略好，并且两者的训练时间基本无异，所以 bert4keras 里边的 MaximumEntropyMarkovModel 默认就是 Bi-MEMM。

思考与拓展

根据上面的结论，在深度学习时代，MEMM 的“没落”似乎就可以理解了——MEMM 除了训练速度快点之外，相比 CRF 似乎也就没什么好处了，两者的预测速度是一样的，而很多时候我们主要关心预测速度和效果，训练速度稍微慢点也无妨。

这两个模型的比较结果是有代表性的，可以说这正是所有全局归一化和局部归一化模型的差异：全局归一化模型效果通常好些，但实现通常相对困难一些；局部归一化模型效果通常不超过全局归一化模型，但胜在易于实现，并与易于拓展。 

如何易于拓展？这里举两个方向的例子。 

第一个例子，假如标签数很大的时候，比如用序列标注的方式做文本纠错或者文本生成时（相关例子可以参考论文 Fast Structured Decoding for Sequence Models [5]），标签的数目就是词表里边的词汇数 |V| ，就算用了 subword 方法，词汇数少说也有一两万，这时候转移矩阵的参数量就达到数亿（），难以训练。

读者可能会想到低秩分解，不错，低秩分解可以将转移矩阵的参数量控制为 2d|V| ，其中 d 是分解的中间层维度。不幸的是，对于 CRF 来说，低秩分解不能改变归一化因子计算量大的事实，因为 CRF 的归一化因子依然需要恢复为 |V| × |V| 的转移矩阵才能计算下去，所以对于标签数目巨大的场景，CRF 无法直接使用。

但幸运的是，对于 MEMM 来说，低秩分解可以有效低降低训练时的计算量，从而依然能够有效的使用。bert4keras 里边所带的 MaximumEntropyMarkovModel 已经把低秩序分解集成进去了，有兴趣的读者可以查看源码了解细节。 

第二个例子，上述介绍的 CRF 和 MEMM 都只考虑相邻标签之间的关联，如果我要考虑更复杂的邻接关联呢？比如同时考虑  跟  的关联？

这时候 CRF 的全局归一化思路就很难操作了，归根结底还是归一化因子难算；但如果是 MEMM 的局部归一化思路就容易进行。事实上，笔者之前设计的信息抽取分层标注思路，也可以说是一种跟 MEMM 类似的局部归一化的概率图模型，它考虑的关联就更复杂化了。

文章小结

本文介绍并简单推广了跟 CRF 一样同为概率图经典案例的 MEMM，它与 CRF 的区别主要是归一化方式上的不一样，接着笔者从实验上对两者做了简单的比较，得出 MEMM 训练更快但效果不优于 CRF 的结论。尽管如此，笔者认为 MEMM 仍有可取之处，所以最后构思了 MEMM 的一些拓展。

相关链接

[1] https://www.aclweb.org/anthology/H05-1059/

[2] https://github.com/bojone/bert4keras

[3] https://github.com/bojone/bert4keras/blob/master/examples/task_sequence_labeling_cws_crf.py

[4] https://github.com/bojone/bert4keras/blob/master/examples/task_sequence_labeling_ner_crf.py

[5] https://arxiv.org/abs/1910.11555

点击以下标题查看更多往期内容： 

• 简明条件随机场CRF介绍 | 附带纯Keras实现
  

• 你的CRF层的学习率可能不够大
  

• 基于DGCNN和概率图的轻量级信息抽取模型
  

• 深度学习预训练模型可解释性概览
  

• 如何快速理解马尔科夫链蒙特卡洛法？
  

• 神经网络中的常用激活函数总结

#投 稿 通 道#

 让你的论文被更多人看到 

如何才能让更多的优质内容以更短路径到达读者群体，缩短读者寻找优质内容的成本呢？答案就是：你不认识的人。

总有一些你不认识的人，知道你想知道的东西。PaperWeekly 或许可以成为一座桥梁，促使不同背景、不同方向的学者和学术灵感相互碰撞，迸发出更多的可能性。 

PaperWeekly 鼓励高校实验室或个人，在我们的平台上分享各类优质内容，可以是最新论文解读，也可以是学习心得或技术干货。我们的目的只有一个，让知识真正流动起来。

📝 来稿标准：

• 稿件确系个人原创作品，来稿需注明作者个人信息（姓名+学校/工作单位+学历/职位+研究方向） 

• 如果文章并非首发，请在投稿时提醒并附上所有已发布链接 

• PaperWeekly 默认每篇文章都是首发，均会添加“原创”标志

📬 投稿邮箱：

• 投稿邮箱：hr@paperweekly.site 

• 所有文章配图，请单独在附件中发送 

• 请留下即时联系方式（微信或手机），以便我们在编辑发布时和作者沟通

🔍

现在，在「知乎」也能找到我们了

进入知乎首页搜索「PaperWeekly」

点击「关注」订阅我们的专栏吧

关于PaperWeekly

PaperWeekly 是一个推荐、解读、讨论、报道人工智能前沿论文成果的学术平台。如果你研究或从事 AI 领域，欢迎在公众号后台点击「交流群」，小助手将把你带入 PaperWeekly 的交流群里。

▽ 点击 | 阅读原文 | 查看作者博客