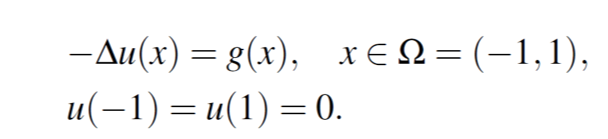F-Principle：初探深度学习在计算数学的应用

2019 年 2 月 28 日 PaperWeekly

作者丨许志钦、张耀宇

学校丨纽约大学阿布扎比分校博士后、纽约大学库朗研究所访问学者

研究方向丨计算神经科学、深度学习理论

在上一篇文章F-Principle：初探理解深度学习不能做什么中，我们介绍了如何用一个统一的框架来初步理解深度学习的优势与局限。在这篇文章中，我们将探索如何利用我们对深度学习已有的理解来设计算法。我们期待这些初步的探索能对解决真实问题起到引导作用。

首先，我们回顾一下这个框架。我们的发现可以用一句话概括：深度学习倾向于优先使用低频来拟合目标函数。我们将这个机制称为 F-Principle（频率原则）。

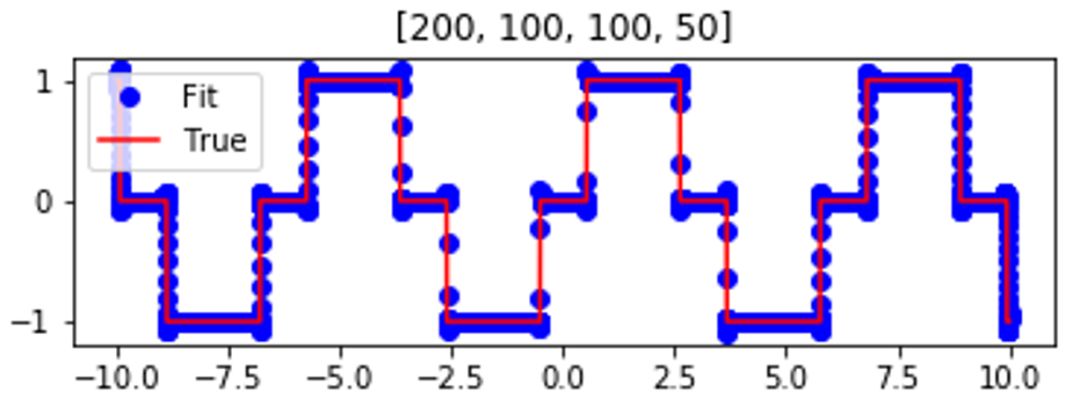
我们先用一个简单的例子来理解 F-Principle。用一个深度神经网络（DNN）去拟合如下的红色实线函数。训练完后，该曲线能被深度网络（蓝色点）很好地拟合。

我们感兴趣的是 DNN 的训练过程。如下图动画所示，红色为目标函数的 FT（傅里叶变换），蓝色为网络输出的 FT，每一帧表示一个训练步，横坐标是频率，纵坐标是振幅。

我们发现，在训练过程中，DNN 表示的函数的演化在频域空间有一个清晰的规律，即频率从低到高依次收敛。

部分读者觉得 F-Principle 非常直观，甚至非常显然（trivial）。部分原因可能是因为 F-Principle 并不是一个陌生的概念，而是我们日常生活中经常都在用的一个原则。想象一下，如果让一个人去记住一个没见过的东西，一般比较粗糙的轮廓信息会先被记住，然后再是很多细节。

没错，DNN 也正是使用了这样的一个学习过程。举一个例子，我们来训练一个 DNN 来记住一张图片。DNN 的输入是一个位置坐标 (x,y)，我们希望它输出这个位置对应的灰度值。

下图的一系列图展示了不同训练步数，DNN 学习到的图像，正如我们前面所猜测的从粗糙的轮廓到细节的学习过程。

然而！更多的人非常惊讶于 DNN 有这样简单的规则。特别地，在计算数学中，很多迭代格式都是先收敛高频，例如 Jacobi 方法和 Gauss–Seidel 方法。由于低频往往是比较重要的，因此高频优先的原则造成了很多苦恼。于是许多研究者手动设计很多算法来提升收敛低频的速度，比如多重网格法。

对于大部分 DNN，它并不需要任何显示的条件或者手动设计，它自然有低频优先的原则。举个例子，考虑如下 Poisson 方程：

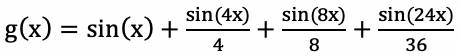
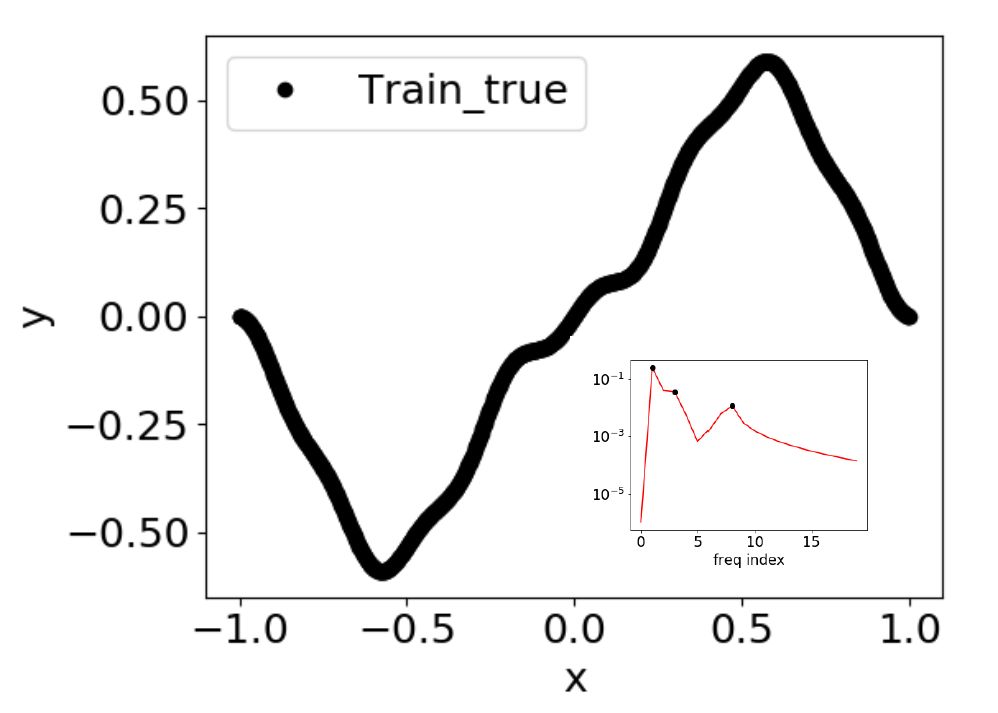
其中，。它的真实解如下图曲线所示：

▲ 黑色为Poisson方程的真解，插图里红色为真解的傅里叶变换

真解中有三个比较显著的频率峰值。如果我们用 Jacobi 迭代去解这个方程，如下图，高频先收敛。

▲ Jacobi迭代：三个重要频率点处的相对误差与训练步数的关系，红色表示相对误差小，高频先收敛

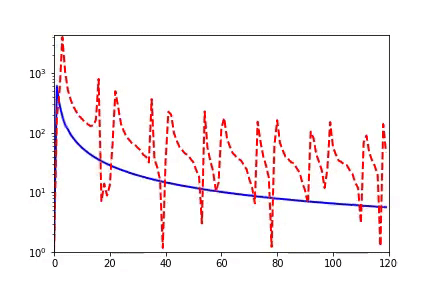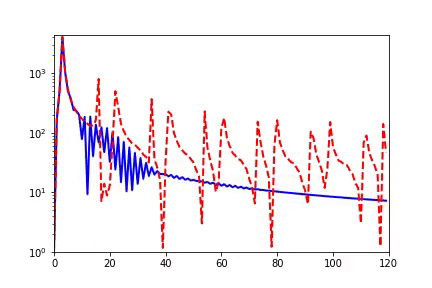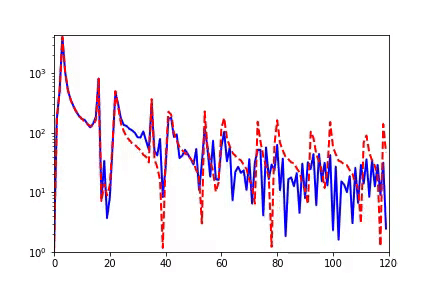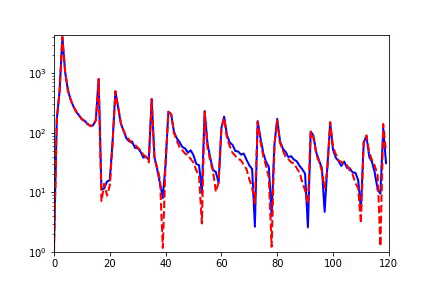
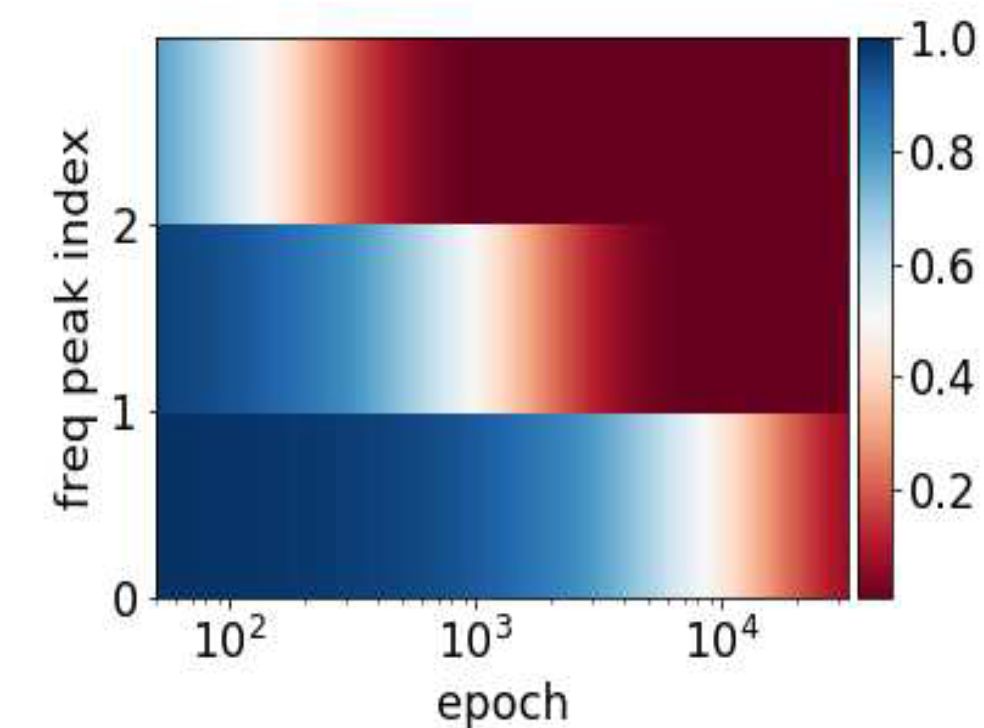
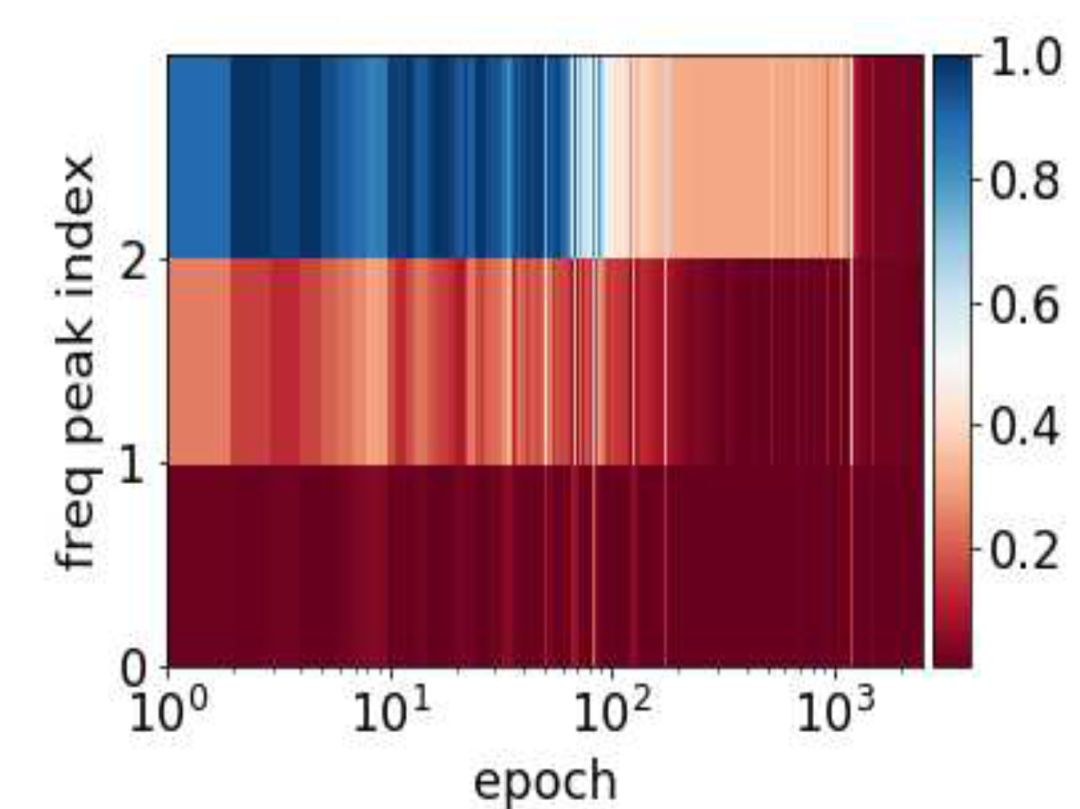
如果我们用 DNN 来解这个方程，我们会得到完全不一样的结果。DNN 的输入为 x，我们用 DNN 的输出去逼近真解 u(x)。损失函数采用 Poisson 方程的能量泛函。具体解的过程可以参见论文。如下图所示，F-Principle 非常明显，既低频比高频收敛得快很多。

▲ 宽度为1-4000-500-400-1的DNN：三个重要频率点处的相对误差与训练步数的关系，红色表示相对误差小，低频先收敛

一个自然的想法是，为了更快地解 Poisson 方程，我们可以先用 DNN 解出低频部分。等低频收敛好以后，将 DNN 的输出作为 Jacobi 迭代的初值来继续解 Poisson 方程。

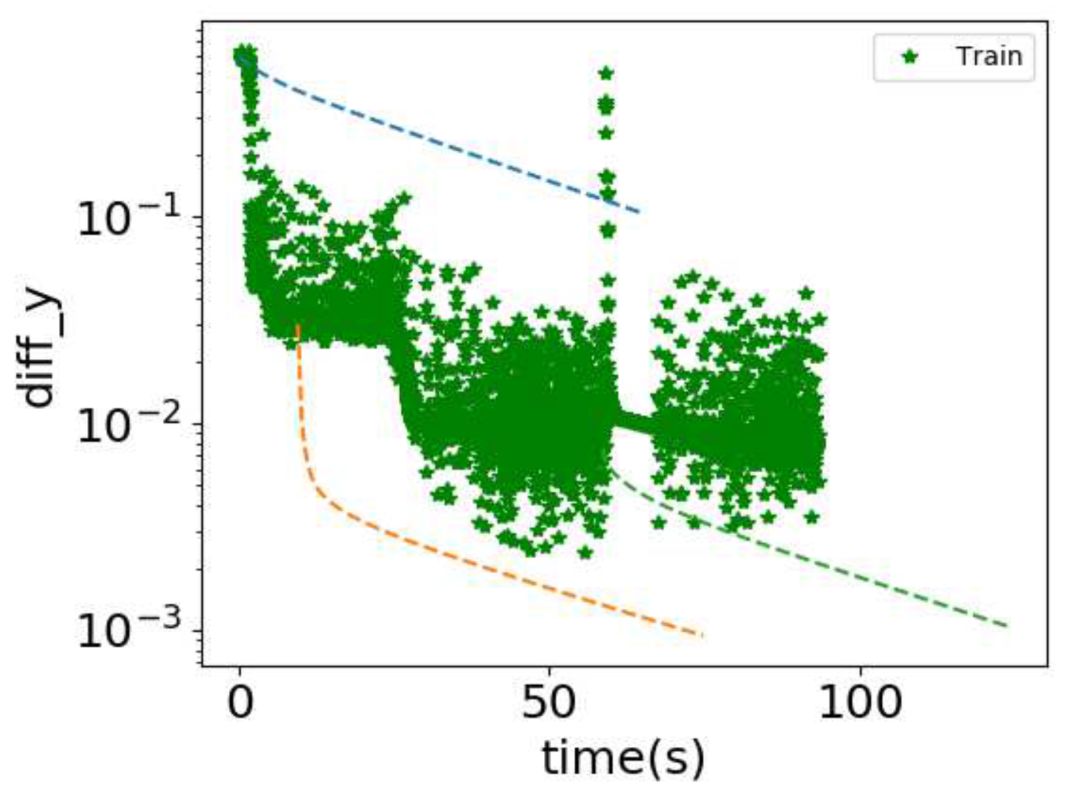
在下图中，我们展示了结合两种方法的效果。下图展示的是数值解和真实解之差的最大绝对值随计算机运行时间的变化。

▲ 结合DNN与Jacobi来解Poisson方程。横坐标：计算机运行时间。纵坐标：数值解和真实解之差的最大绝对值。绿色星号：DNN的结果。虚线：Jacobi方法继续运算的结果，不同虚线表示选择不同DNN训练时刻的输出作为初值

如果单纯使用 DNN，绿色星号表明在一段时间后，DNN 的输出振荡很厉害。三条虚线的结果是在不同时刻使用 Jacobi 继续运算的结果。最左边的蓝色虚线选择的时刻过早，导致 Jacobi 方法需要花大时时间来收敛低频，因此误差下降很慢。最右边的绿色虚线选择的时刻过晚，导致大量时间花在 DNN 收敛高频上。中间的橙色虚线刚好利用了 DNN 收敛好的低频，并且马上使用 Jacobi 方法快速收敛高频，所以误差在短时间内能下降最快。

在偏微分方程的数值问题中，有很多问题对于传统算法是很困难的。很多研究工作已经开始探索如何使用 DNN 来解这些问题。

这个例子只是一个非常简单地情况，对于用 F-Principle 的理解来帮助 DNN 应用在更复杂、更高维的问题中，仍然有非常多值得探讨的问题。这个例子展示了在理解 DNN 的基础上去使用 DNN，我们可以既利用 DNN 的强项，又能避免 DNN 的弱点。

参考文献

Xu, Zhi-Qin John; Zhang, Yaoyu; Luo, Tao; Xiao, Yanyang & Ma, Zheng (2019), ‘Frequency principle: Fourier analysis sheds light on deep neural networks’, arXiv preprint arXiv:1901.06523.