【ACL 2019 】Facebook：从文本语料库中构建术语的分类结构

【导读】针对从大型文本语料库中推断is-a关系的任务，本篇论文提出了一种结合双面嵌入和Hearst模型的新方法。这种方法可以设置适当的约束条件，以便从上下文中推断出分类结构，同时还能纠正错误的is-a关系。

下载地址：

https://www.zhuanzhi.ai/paper/d6b1f7e7fecf2d2ea60d4e13c4f0aa46

01

介绍

作者提出了一种无监督的方式，并结合Hearst模型和双曲嵌入。Hearst模型基于一些规则或者模板去做抽取，从而获得上下位关系，然而，Hearst模型特别容易丢失或者提取错误的上下位关系，因此，在本文中，首先使用Hearst模型来提取语料库中潜在的is-a关系，然后从候选库中构建有向加权图，然后将此图嵌入到双曲空间中，以推断缺失的上下位关系并删除错误的is-a关系。这种方法的优势有以下几点：

• 一致性：双曲线嵌入可以使整个嵌入空间中强制实现is-a关系的传递性，这样就提高了模型的分类一致性。因为如果（x; is-a; y）和（y; is-a; z）强制执行（x; is-a; z）

• 有效性：双曲空间允许具有较低的嵌入，在实验中，我们将显示双曲线嵌入使我们可以将嵌入维数减少一个数量级，同时胜过基于SVD的方法。

• 可解释性：在双曲嵌入中，相似性是通过距离获取的，而分类等级是通过嵌入获取的，除了语义相似性以外，还可以获取通用术语。

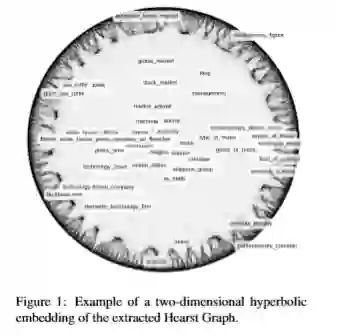
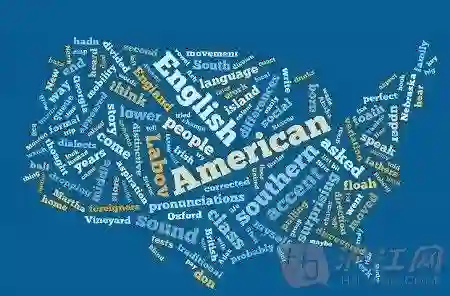
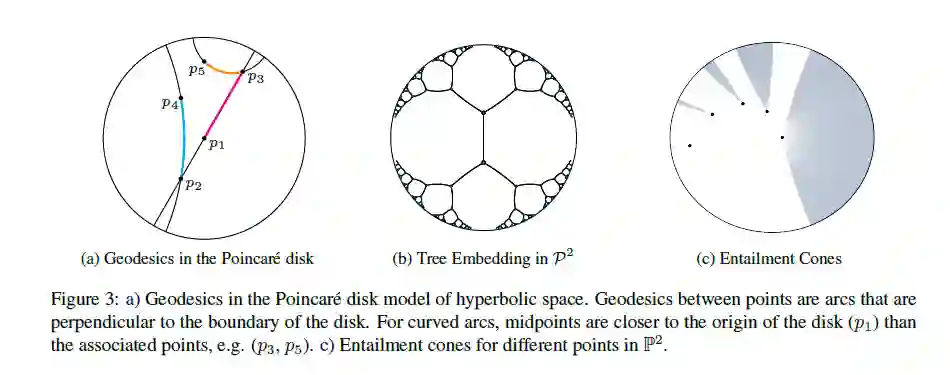
figure1显示了Hearst的二维嵌入示例，尽管再最终的嵌入中使用更高的维度，但可视化可以很好的说明通过嵌入获取的等级结构。

02

相关工作

上位词探索

在自然语言处理中，从文本中检测“is-a”关系是一项长期的任务。一种流行的方法是利用Hearst（Hearst，1992年）首先提出的高精度词汇句法模式。这些模式可以预先定义或自动学习（Snow等，2005；Shwartz等，2016）。但是，众所周知，这种基于模式的方法会因缺少提取而遭受重大损失，因为术语必须以正确的关系出现才能被检测到。最近的工作通过利用搜索引擎（Kozareva和Hovy，2010）或利用网络规模的语料库（Seitner等，2016）来提高覆盖率。为了克服基于模式的方法的稀疏提取，近来的重点已转移到分布方法。这些方法减轻了稀疏性问题，但是还需要专门的相似性度量来区分不同的词汇关系。迄今为止，大多数度量都是受分布包容性假设（DIH；Geffet and Dagan 2005）的启发的，基于分布方法的无监督的方法包括WeedsPrec（Weeds等人，2004），invCL（Lenci和Benotto，2012），SLQS（Santus等人，2014）和DIVE（Chang等人，2018）。基于位置或基于依存关系的分布表示也可能捕获类似Hearst模式的粗略特征（Levy等人，2015；Roller和Erk，2016）。Shwartz等 （2017年）表明，这样的环境对于分配方法的成功起着重要的作用。最近，Roller等人 （2018）对无监督分布和基于模式的方法进行了系统研究。他们的研究结果表明，基于模式的方法在一些具有挑战性的上位基准上能够胜过基于DIH的方法。良好性能的关键方面是从大型文本语料库中提取模式并使用嵌入方法来克服稀疏性问题。我们的工作基于这些发现，将其嵌入替换为具有自然分层的几何结构的嵌入。

分类归纳

尽管探索上位词关系是一项重要且困难的任务，完整的分类归纳是一项并行且互补的任务，该领域的许多工作都将分类图作为起点，并通过多种方法来扩展分类图。

嵌入

该领域提出了许多方法，最近的工作集中在单词类复杂的重叠结构上，并使用盒格结构（Vilnisetal，2018）和高斯单词嵌入（Athiwaratkun和Wilson，2018）来诱导层次结构。与许多纯粹基于图的作品相比，这些方法通常需要对层次结构进行广泛的监督，并且无法仅使用非结构化的噪声数据来学习分类法。最近，Tifrea等 （2018）提出将GLOVE（Pennington 2014）扩展到双曲空间。我们在第4节中的实验结果显示，Tifrea （2018）报告对于hypernymyy预测而言具有可观的收益，强调了为此任务选择正确的分布环境的重要性。

03

方法

此部分，我们将讨论无监督学习的分类方法，首先是hearst的提取和构建，然后是双曲线嵌入。

Hearst图结构

Hearst中的主要思想是利用某些词汇句法模式来检测is-a关系，比如：NPy such as NPx，或者NPx and other NPy表示的就是is-a关系。将名词短语视为有向图节点，通过使用非结构化文本和有限的先验知识来构造Hearst图，Table1中列出了本文中使用的句子模型，用E={u,v}来表示获取到的上下位词对，用w(u,v)来表示它们之间的关系。

但是Hearst生成的图存在许多错误，例如生成的图中包含一下循环：（区域，is-a，spot ），（spot ，商业），（商业，促销），（促销，区域）。

双曲嵌入

首先，将简要介绍双曲嵌入的 概念，与欧几里得空间或球面空间相反，它存在多个等价的双曲面空间模型，由于这些模型之间可以转换，因此保留所有几何特征。对于给定的任务，我们可以选择最合适的一个。接下来，首先讨论基于Poincare-ball的模型，Poincare-ball是指Riemannian manifold：

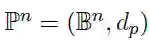
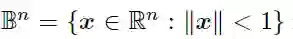
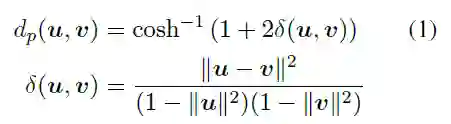
B是n维的单位球，d_p是个距离函数。

双曲空间具有分层结构，在Poincare-ball模型中比较明显，靠近圆盘原点的点相对于球中的所有其他点相对较近，而靠近边界的点则相距较远，距离是学习分类结构连续性的关键，并且与书中最短路径相对应。

Hyperbolic Entailment Cones（HEC）

HEC的主要思想是为空间中的每个点定义一个双曲线锥Cv形式的包围区域，位于Cv中的点u就是v的子集，每个Cv的宽度是由基点的L范数||v||确定的，v越接近原点，基点就越通用，Cv的宽度就越大，包含的术语就越多，并定义了一个能量函数：

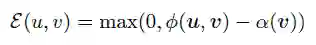
a(v)表示与点v相关的圆锥的半孔，而φ(u，v)表示之间的half-lines角度，u属于 Cv，则能量函数为0，反之能量函数可以解释为u进入v的最小旋转角度。

给定一个Hearst图G=(V,E,w)，采用以下方法计算所有术语的embedding：v_i表示术语i的嵌入。为了最小化词嵌入的能量，我们采用以下方法：

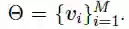
等式3是为了找到 所有术语的联合嵌入。

Lorentz Entailment Cones

从优化的角度看，Poincar´e-ball模型并不是最优的，因为当点靠近接近球的边缘的时候，容易出现数值不稳定，因此我们在Lorentz模型中进行优化。Lorentz 模型被定义为：

n维双曲空间的Lorentz模型就是黎曼流形：

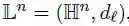
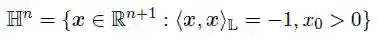
表示n维双曲面的上层，其中L的相关距离函数为：

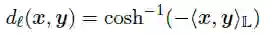
由于两个模型的等效性，我们可以在两个空间之间定义一个映射，以保留所有属性， Lorentz 模型中的点可以映射到Poincar´e-ball中:

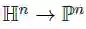
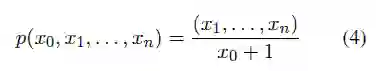
此外，P^n的点可以映射到L上，通过以下计算：

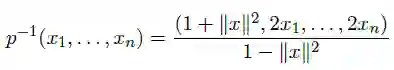
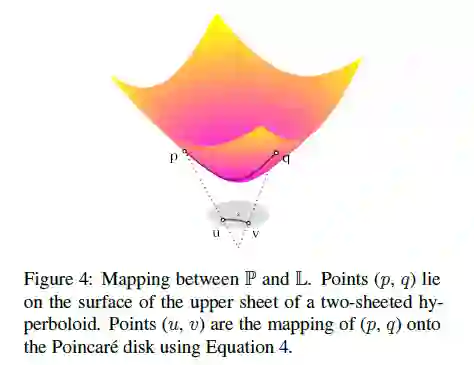
为了在Lorentz 模型上定义entailment cones，必须在L^n上推导a(v)和φ(u,v)，我们可以从余弦的双曲定律和P与L之间的映射获得：

04

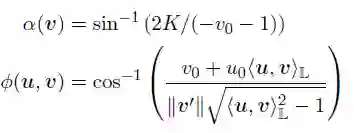
实验

为了评估方法的有效性，我们比较了以下模型：

基于模式的模型 设置E为Hearst模型，w(x,y)是（x,y）在E中出现的次数，我们采用以下模型方法：

• Count Model(p)，该模型进输出计数，或等效的输出Hearst模型的概率：

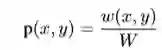
• PPMI Model(p)，为了校正偏斜的出现概率，PPMI模型基于Hearst语料库上的PMI预测了上位关系。

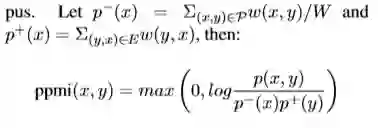
• SVD Count(sp)，对于丢失的关系，我们用基于Hearst SVD对比了低排名的嵌入，然后计算：

这里X_ij=w(i,j)/W。

• SVD PPMI (spmi)，我们还对PPMI矩阵的SVD进行了评估，该值与sp相同。

双曲嵌入(HypeCone)，我们将Hearst图嵌入到双曲空间，在评估时，使用模型能量E预测可能性。

分布模型

我们基于DIH，一个小范围术语应该是大范围术语的子集。采用以下几种方法：

• WeedsPrec，获取的x特征应该包含在更广泛的术语的特征集中：

• invCL，通过计算广义术语包含狭义术语的程度：

  
  

• SLQS，该模型基于信息假设（一般单词出现在非信息性上下文中），即通过熵：

语料库与处理过程

我们采用Roller et al, 2018中的数据，Hearst模式是从GigaWord和Wikipedia的串联中提取的。最终语料库包含大约4.5M个匹配对，431K个唯一对和243K个唯一项。

上下位任务

我们考虑了三个截然不同的子任务，用于评估这些模型的预测性能：

• 检测：给定一对单词（u，v），确定v是u的上位词

• 方向：给定一对单词（u，v），判断u比v更加通用

• 等级：给定一对单词（u，v），确定u是v的上位词的程度

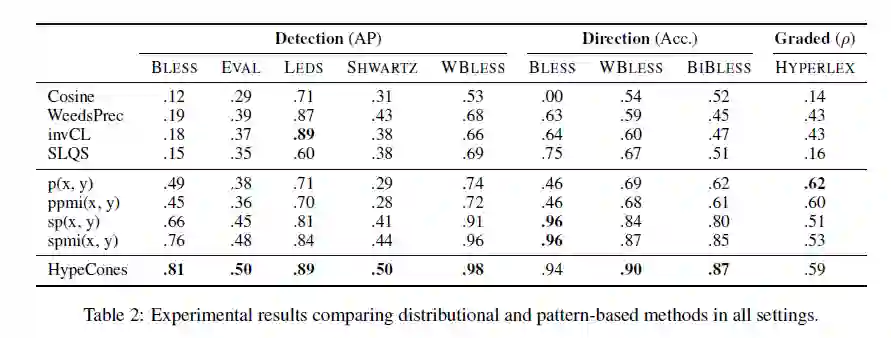
为了进行检测，我们评估了五个常用基准数据集上的所有模型：BLESS（Baroni和Lenci，2011），LEDS（Baroni等，2012），EVAL（Santus等，2015），SHWARTZ（Shwartz等,2016年）和WBLESS（Weeds等人，2014年）。Table 2为对比试验结果。

05

结论

在这项工作中，我们提出了一种从大型文本语料库推断术语分类结构的新方法。为此，我们将Hearst模式与双曲线嵌入相结合，这使我们能够对分布上下文设置适当的约束并提高嵌入空间的一致性，双曲空间的自然层次结构使我们还可以学习非常有效的嵌入，从而大大降低了基于SVD的方法所需的维数。为了提高优化效果，我们还提出了一种新的方法来计算双曲空间的Lorentz模型中的蕴含锥度，实验显示，我们的方法在分类构建上达到了最新性能。

更多干货请上专知网站，获取查看

https://www.zhuanzhi.ai/topic/2001227667643246/awesome

-END-

专 · 知

专知，专业可信的人工智能知识分发 ，让认知协作更快更好！欢迎注册登录专知www.zhuanzhi.ai，获取5000+AI主题干货知识资料！

欢迎微信扫一扫加入专知人工智能知识星球群，获取最新AI专业干货知识教程视频资料和与专家交流咨询！

点击“阅读原文”，了解使用专知，查看5000+AI主题知识资料