ICML 2020 | 4 篇图卷积网络相关论文

本文介绍 ICML2020 中 4 篇与图卷积网络相关的论文。

论文	亮点
1. 自监督何时有助于图卷积网络？	首次将自监督纳入 GCNs 的系统探索和评估
2. 用于图结构数据的卷积核网络	引入了一族多层图核，并在图卷积神经网络和核方法之间建立了新的联系
3. 简单和深图卷积网络	设计与分析了深图卷积网络
4. 常曲率图卷积网络	提出图卷积网络到常曲率空间的数学基础概括

1. When Does Self-Supervision Help Graph Convolutional Networks?

https://proceedings.icml.cc/static/paper_files/icml/2020/1185-Paper.pdf

这项研究首次将自监督纳入 GCNs 的系统探索和评估。

• 首先阐述了 将自监督纳入 GCNs 的三种机制，分析了预训练 & 微调和自训练的局限性，并进而将重点放在多任务学习上。
• 此外提出了 三种新的 GCNs 自监督学习任务，并进行了理论分析和数值比较。
• 最后进一步 将多任务自监督融入到图对抗训练中。

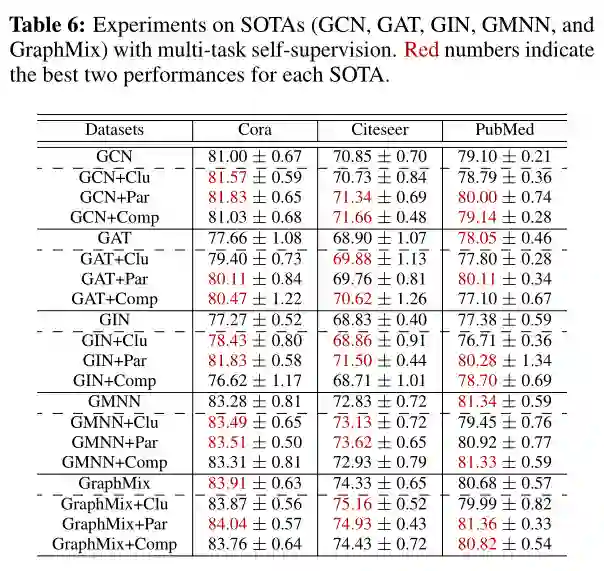
研究结果表明，通过合理设计任务形式和合并机制，自监督有利于 GCNs 获得更强的泛化能力和鲁棒性。论文代码可以在 https：//github.com/shen-Lab/SS-GCNS 上获得。

通过多任务学习对 GCN 进行自监督的总体框架。目标任务和辅助自监督任务共享相同的特征提取器

三个自监督任务概述

在SOTAs（GCN、GA T、GIN、GMNN 和 GraphMix）上进行多任务自监督的实验。红色数字表示每个 SOTA 的最好的两个结果

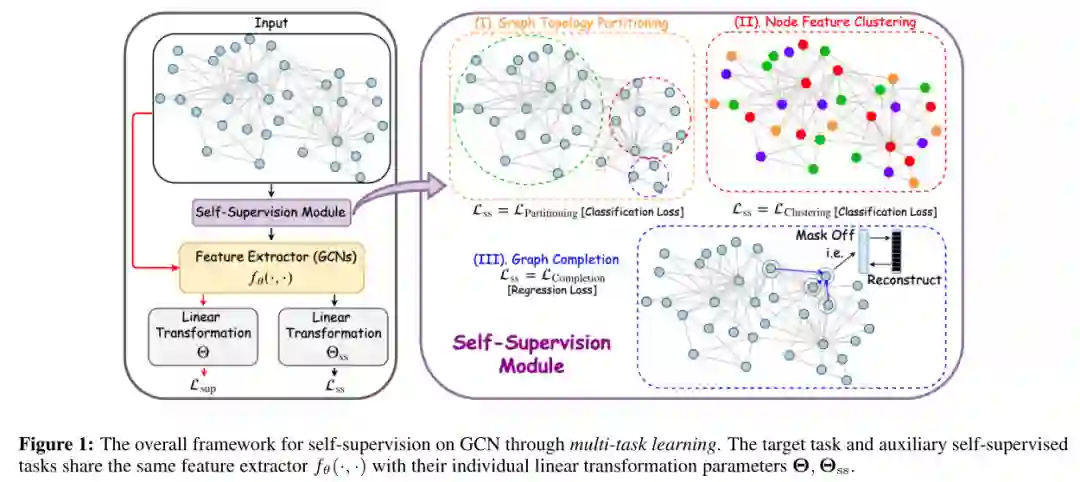
2. Convolutional Kernel Networks for Graph-Structured Data

https://proceedings.icml.cc/static/paper_files/icml/2020/1656-Paper.pdf

这篇文章引入了一族多层图核，并在图卷积神经网络与核方法之间建立了新的联系。

• 通过将图表示为核特征映射序列（其中每个节点携带关于局部图子结构的信息），文章中的方法 将卷积核网络推广到图结构数据。
• 一方面，核的观点提供了一种无监督的、有表现力的、易于正规化的数据表示，这在样本有限的情况下很有用。
• 另一方面， 提出的模型也可以在大规模数据上进行端到端的训练，从而产生了新型的图卷积神经网络。

实验表明，提出的方法在几个图分类基准上取得了与之相当的性能，同时提供了简单的模型解释。代码可以在 https://github.com/claying/GCKN 中获得。

给定图 ，由 构造图特征映射

具有离散节点属性的图的分类精度

具有连续属性的图的分类精度

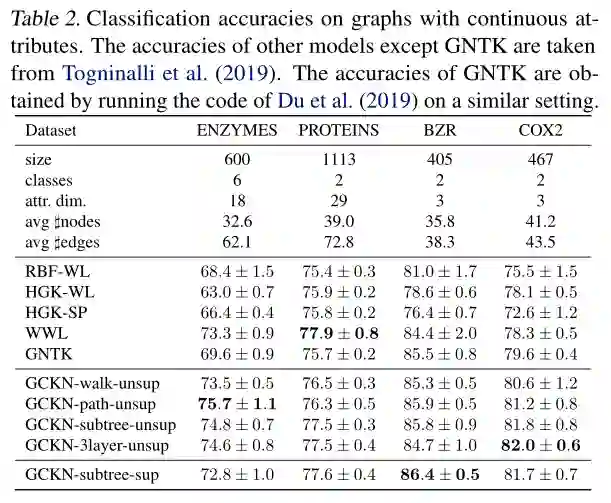
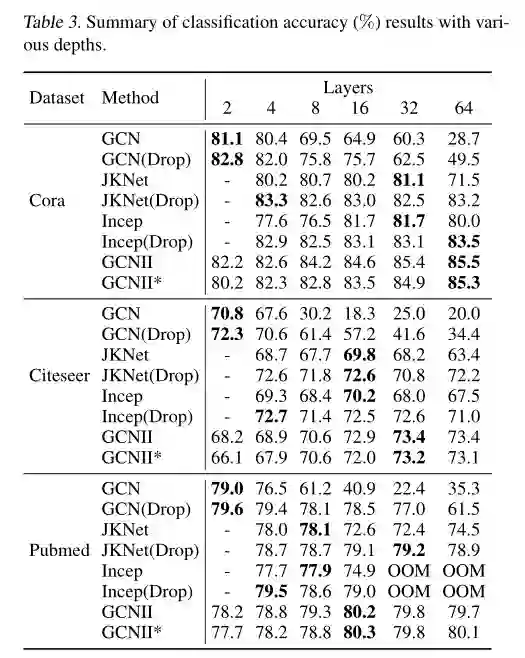
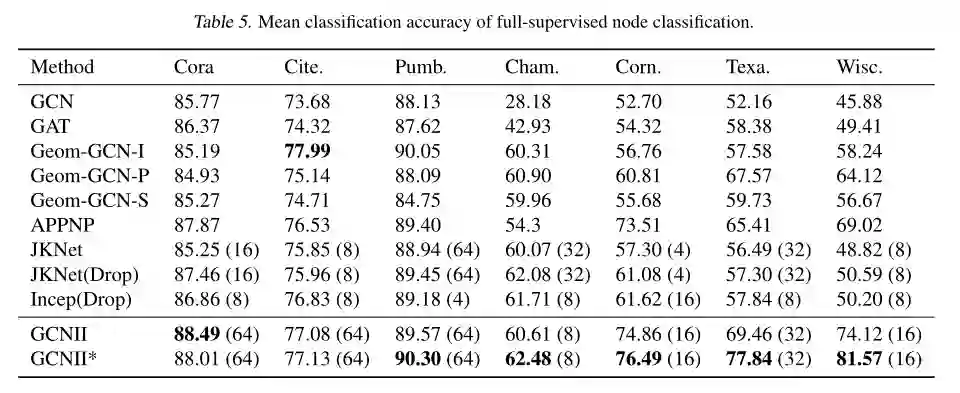
3. Simple and Deep Graph Convolutional Networks

https://proceedings.icml.cc/static/paper_files/icml/2020/2172-Paper.pdf

由于过平滑的问题，目前的大多数图卷积网络(GCNS)模型都很浅。这篇文章研究了深图卷积网络的设计与分析问题。

• 提出了 GCNII 模型，它是对普通 GCN 模型的扩展，使用了两个简单而有效的技术： 初始残差和 单位映射。
• 提供了理论和经验证据，证明这两种技术有效地 缓解了过平滑问题。

实验表明，深度 GCNII 模型在各种半监督和全监督任务上的性能优于最先进的方法。

半监督节点分类—不同深度的分类精度(%)

有监督节点分类—平均分类精度(%)

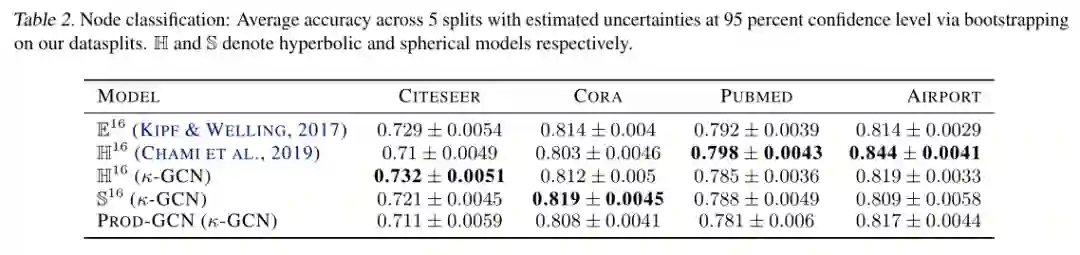
4. Constant Curvature Graph Convolutional Networks

https://proceedings.icml.cc/static/paper_files/icml/2020/5188-Paper.pdf

文章通过

1. 引入允许在所有常曲率几何之间进行可微插值的统一形式
2. 利用 Gyro 重心坐标来推广经典的欧几里得质心概念

提出图卷积网络（GCN）到常曲率空间的数学基础概括。

当曲率从两边变为零时，提出的模型可以平滑地恢复它们的欧几里得变体。实验证明，对于表现出非欧几里德行为的符号数据，根据它们的离散曲率，提出的方法在节点分类和失真最小化任务上优于欧几里德 GCNs。

往期 ICML 2020 论文推荐：

ICML 2020 | 4 篇推荐系统相关论文

---

喜欢的话请点 赞👍 + 在看😳 噢！（✪ω✪）

(๑•̀ㅂ•́)و✧     (๑•̀ㅂ•́)و✧    (๑•̀ㅂ•́)و✧