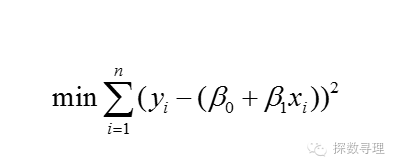统计挖掘那些事（五）--（理论+案例）如何通俗地理解极大似然估计？

点击上方蓝色字体，关注我们

作者简介

浩彬老撕，R语言中文社区特邀作者，好玩的IBM数据工程师，立志做数据科学界的段子手。

个人公众号：探数寻理

往期回顾：

统计挖掘的一些事一些情（一）

统计挖掘的一些事一些情（二）——回归分析（附数据）

统计挖掘那些事（三）-超详尽回归分析指南（理论+动手案例）

统计挖掘那些事（四）-9个相关R先生的故事（理论+动手案例）

极大似然估计最早在1821年首先由咱们的数学王子，高斯所提出。不过人们普遍认为这一方法的广大应用还是主要归功于，现代统计学的奠基人之一，英国统计学习费舍尔。从1912年起，他建立了以最大似然估计为中心的点估计理论。

实际上，极大似然估计很直观，按照字面理解，极大似然估计的意思就是最大那种可能的估计。而这种思想，不夸张地说，在咱们日常生活中也是充满了极大似然估计的身影。

咱们举个例子：

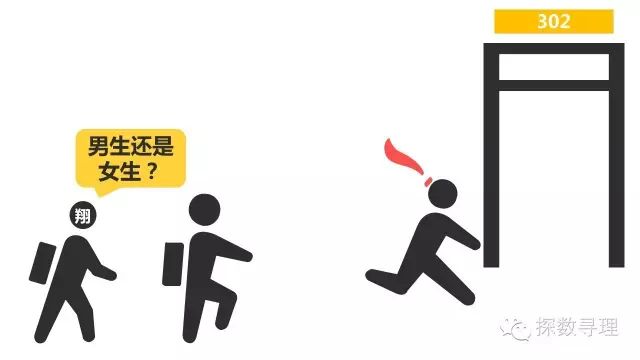
假如有一天你和基友阿翔在上学的途中，看到有一个前面一个身影进了你们等下正要上课的教室。前面的身影走得比较快，你仅仅看到是ta有一把长发。这个时候，你的基友阿翔问你，“咦，前面这个同学走得很快哦，没有看清，是男生还是女生？”

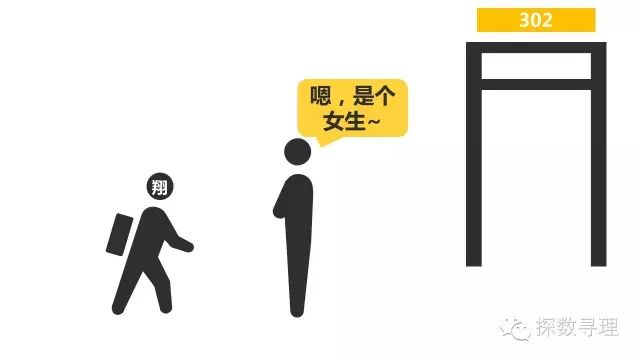
于是，你站在路上想了一下，酷酷地回答说，“是个女生”。

好了，这确实是一个极大似然估计思考的过程，让我们简单回顾一下：

你看到了一个人走进课室，并且看到ta是长头发的。尽管这个同学可能是男的，也可能是女，但是你根据经验判断，女生的长头发的可能性有95%，男生长头发的可能性只有4%，于是，你根据这个可能性做出了判断，她是一个女生。没错，这种按照可能性最大的猜测正是极大似然估计的思想。

好了，接下来，让我们正式定义极大似然估计方法：

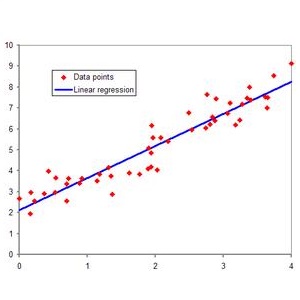
接下来，我们不妨把极大似然估计应用在一元回归分析中进行举例，同时也可以与最小二乘法结果进行比较：

留意到，对于上式最大值，也就是我们需要对右边部分取得最小值，也即

这与我们最小二乘法的目标是完全一致的！这显然是一个有趣的结果。

值得注意的是，在极大似然估计中，我们是假定了随机误差需要服从正态分布，这也提示我们，对于极大似然估计，我们的结果是对我们对于随机变量所假设的概率分布有依赖性的，因此也就要求我们要有一定的先验知识。

最后，咱们简单总结一下极大似然估计的步骤：

((1)根据概率密度函数写出似然函数；

(2)对似然函数取对数，并整理；

3)对对数似然函数求解最大值（一般可以通过求导数解得）；

大家都在看

2017年R语言发展报告（国内）

R语言中文社区历史文章整理（作者篇）

R语言中文社区历史文章整理（类型篇）

公众号后台回复关键字即可学习

回复 R                  R语言快速入门及数据挖掘 
回复 Kaggle案例  Kaggle十大案例精讲（连载中）
回复 文本挖掘      手把手教你做文本挖掘
回复 可视化          R语言可视化在商务场景中的应用 
回复 大数据         大数据系列免费视频教程 
回复 量化投资      张丹教你如何用R语言量化投资 
回复 用户画像      京东大数据，揭秘用户画像
回复 数据挖掘     常用数据挖掘算法原理解释与应用
回复 机器学习     人工智能系列之机器学习与实践
回复 爬虫            R语言爬虫实战案例分享