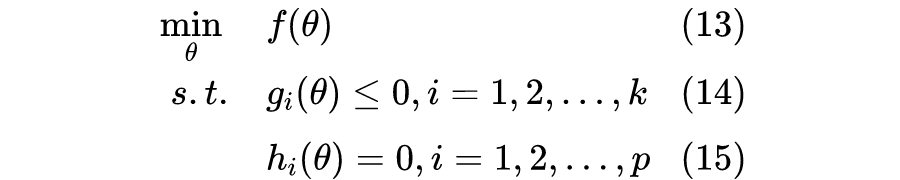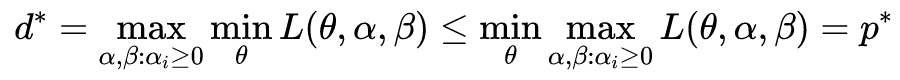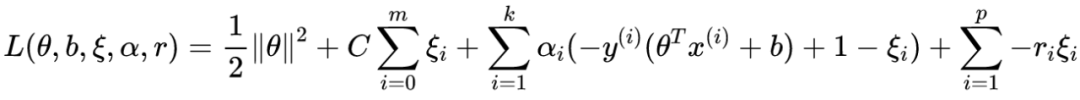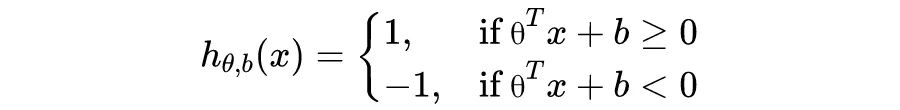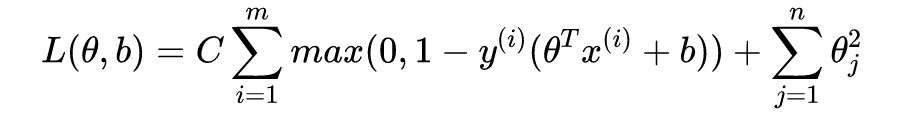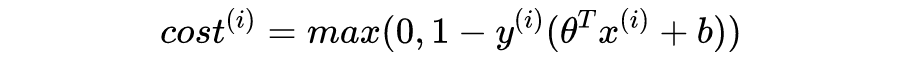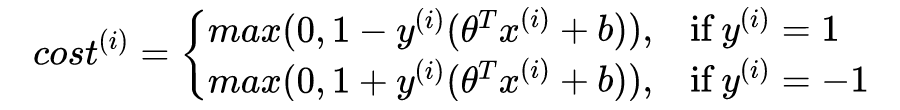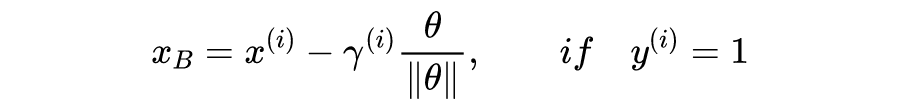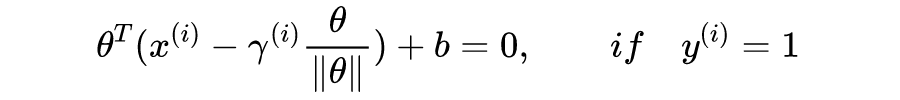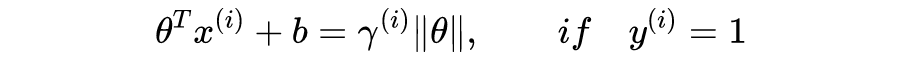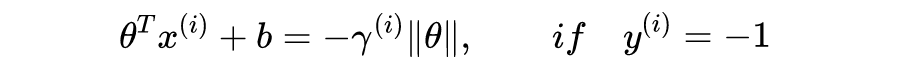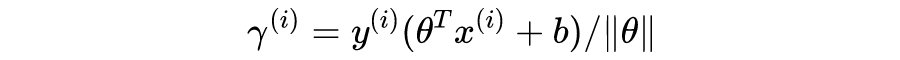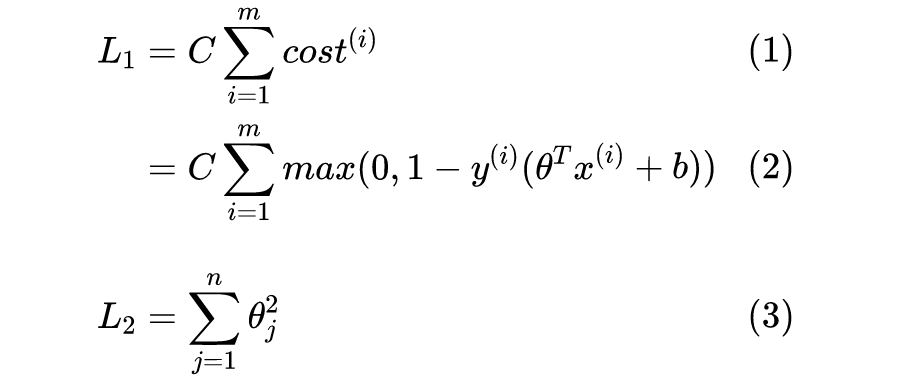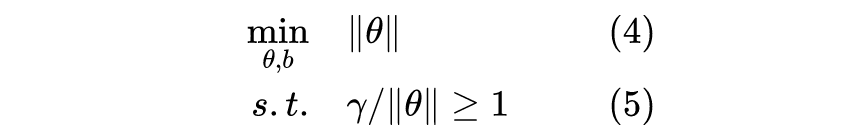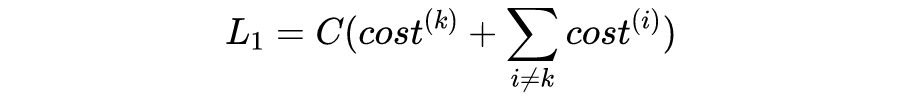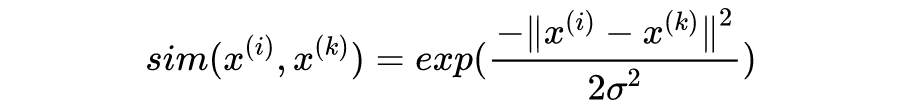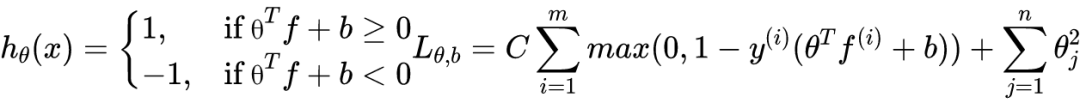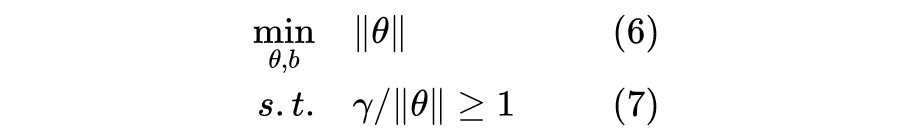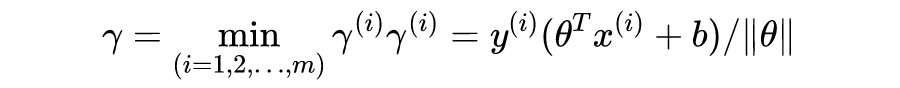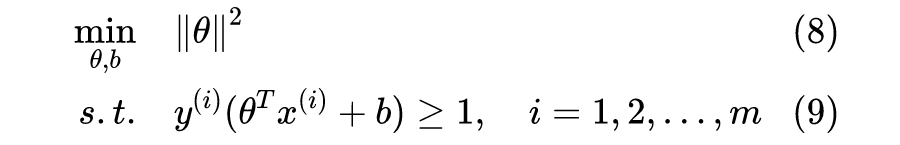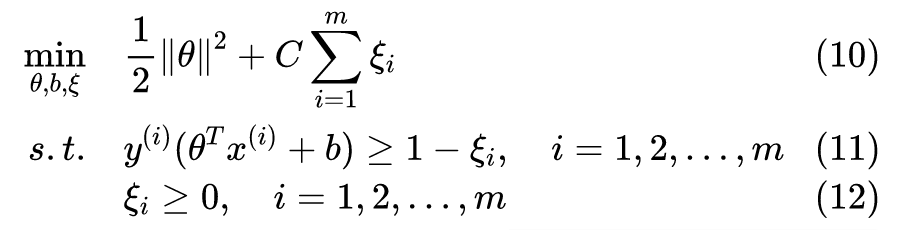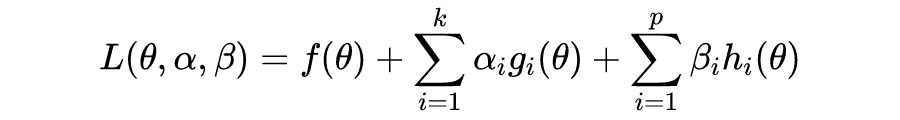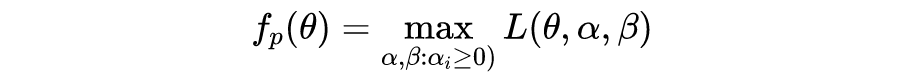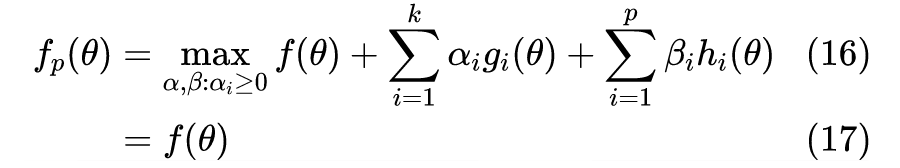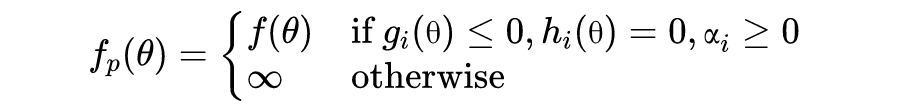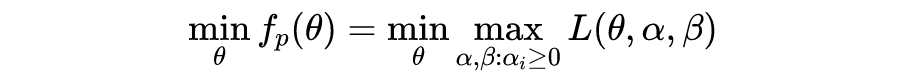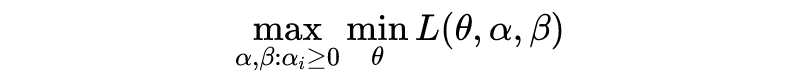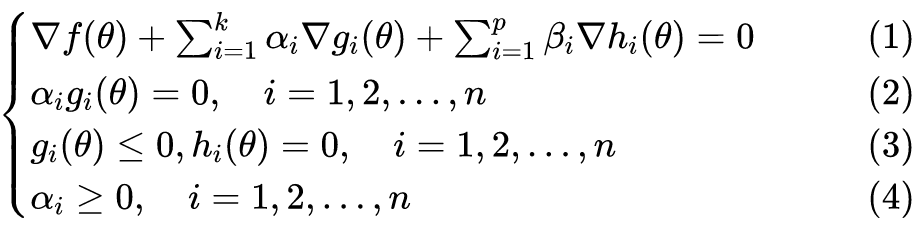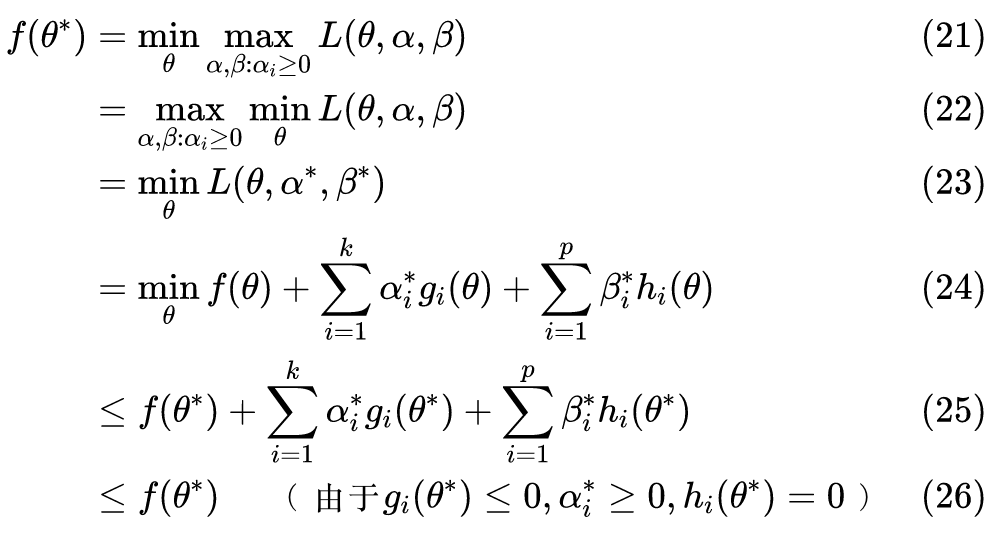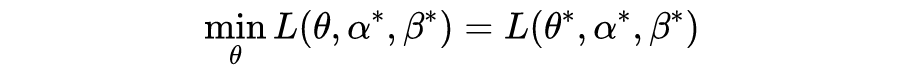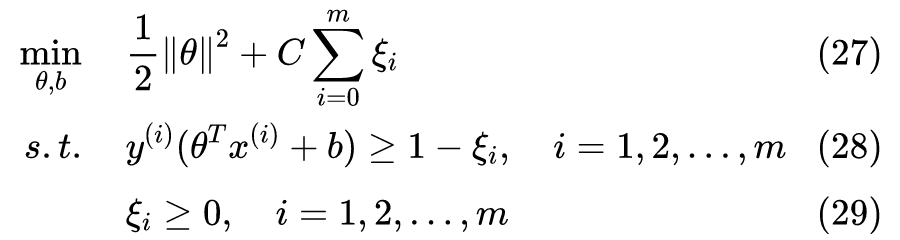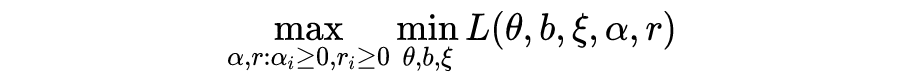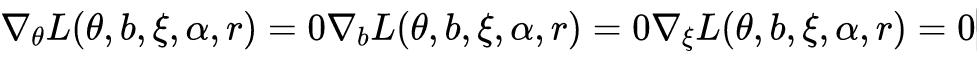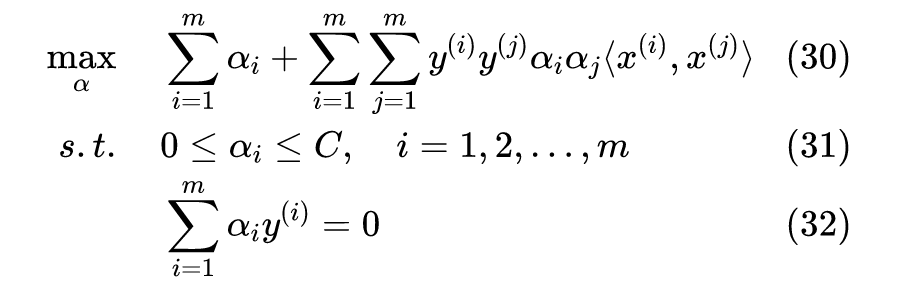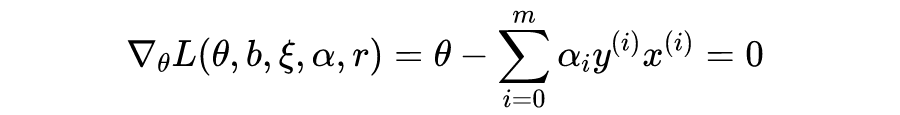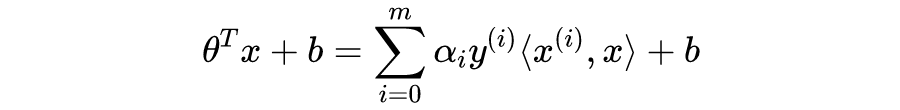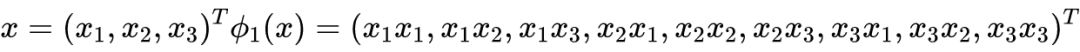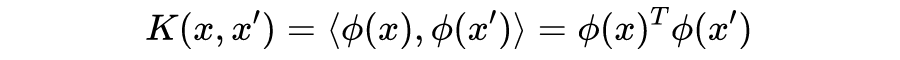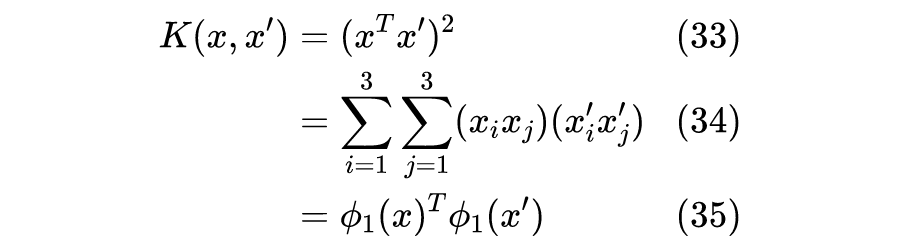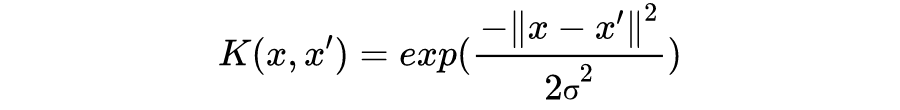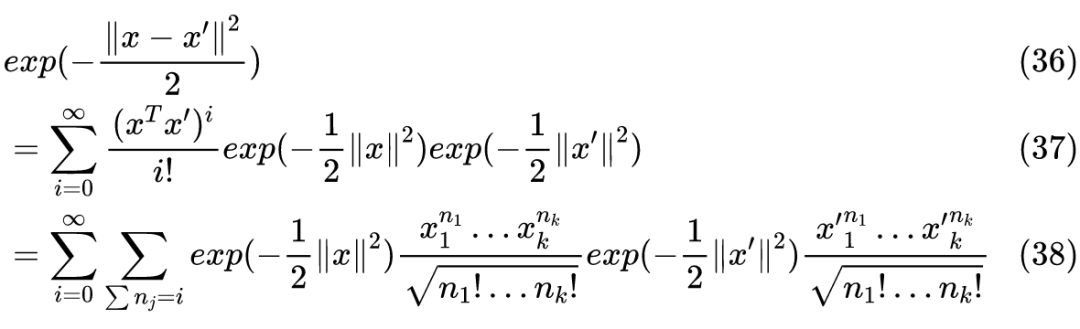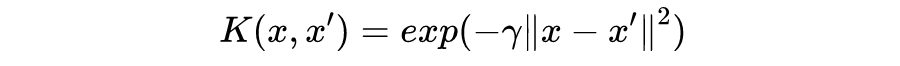一文详解支持向量机（SVM）

©PaperWeekly 原创 · 作者｜王东伟

单位｜Cubiz

研究方向｜深度学习

本文介绍支持向量机（Support Vector Machine，SVM）。

在上一篇文章关于逻辑回归的叙述中，我们提到了决策边界（decision boundary），它实际上是分割 n 维数据点的一个超平面（hyperplane），比如 n=2 时决策边界为直线，n=3 为平面，n=4 为三维“平面”（有三个维度的超平面）。一般来说，n 维空间的超平面有 n-1 个维度，并且可以把空间分割为两个部分。

严格上，“分割空间”是仿射空间超平面的性质，其他空间类型则未必，更多的细节请参阅 Hyperplane. Wikipedia。

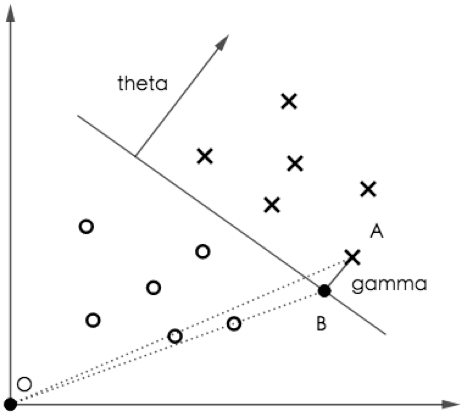
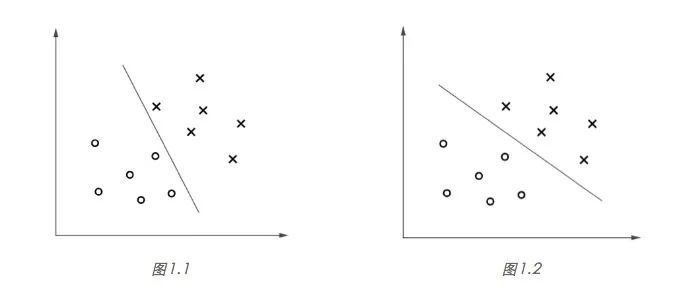
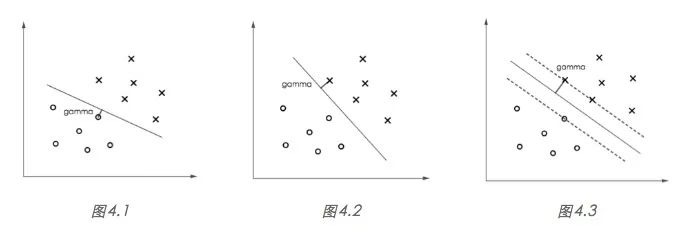
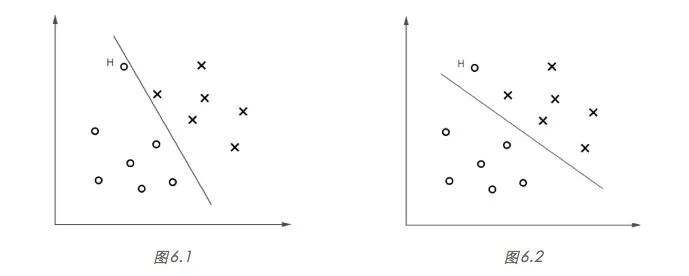
SVM 算法的目标，是找到一个超平面分割不同类别的数据点，并且使得数据点与超平面的最小距离最大。听起来有些拗口，接下来我们以一个简单的例子说明，如图 1 所示，“x”表示正类样本，“o”表示负类样本。

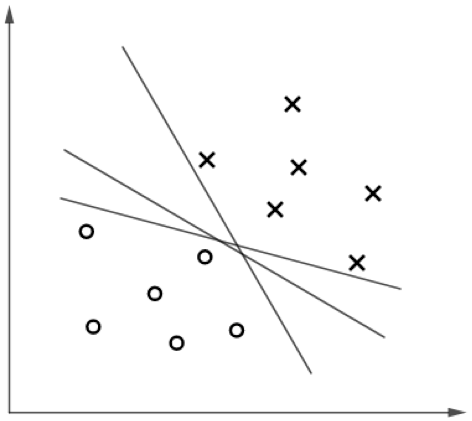
显然，图 1.2 所示的决策边界具有更大的“间隔”（margin），通常具有更稳定的分类性能。粗略地说，大间隔分类器对于未知样本的分类准确率具有更大的均值和更小的方差，比如对于图 1.1 的决策边界，未知的正类样本很大概率会“越过”边界而被错误分类，而图 1.2 的 决策边界则给了未知样本“更大的容错空间”。

关于如何得到最大间隔的决策边界，本文后半部分有较严格的数学推导，不过现在先以“提出假设、设定误差函数、求极值点”的思路来理解 SVM 的原理。

对于上述二分类问题，SVM 算法的步骤如下：

1. 假设：
2. 误差函数：
3. 求 极值点：

其中 C 为常数，暂时无需理会。注意到，SVM 直接给出样本的分类 y = 1 或者 y = -1，而逻辑回归是给出 y = 1 的概率。其中：

等价于：

这也正是我们使用 {1, -1} 表示正负类的原因，可以让 有更简洁的表达。

支持向量机的几何意义

接下来，我们将从几何的角度理解支持向量机。

▲ 图2

如图 2， 是分割正负类样本的直线。A 点为正类样本（即 ），坐标为 ，AB 为垂线段， 为 A 到直线的距离。不难证明向量 垂直于直线。由于 ，并且 （因为 为单位向量），得到点 B 的坐标：

点 B 位于直线上，即：

整理得到：

同理，对于负类样本可以得到：

进一步得到：

需要指出的是，以上推导基于样本是线性可分的情况（即存在一条线性边界可以完美区分两类数据点），其他情况稍后探讨。

回到误差函数。我们把它分成两部分：

观察 表达式，对于正类样本，如果我们希望 ，只需满足 ，即 ；对于负类样本同样可以得到 时， 。

注意到，对于任意一条以 100% 正确率分割正负类样本的直线 ，等比缩放 和 仍然得到同一条直线，意味着我们可以任意调节 ，使得对于任意样本都有 ，即 。因此，如果我们暂时忽略 ，仅仅让 取得极小值，我们可以得到无数条符合条件的决策边界。

▲ 图3

图 3 显示了其中三条满足 取极小值的决策边界。

现在同时让 取得极小值。注意到 ，即我们需要保持 的同时，让 尽可能小。因为 表示数据点到直线的距离，事实上我们只需关注距离直线最近的点，令 ，则优化目标为（再次强调，仅对于线性可分的情况）：

我们来看几个直观的例子：

显然，图 4.3 的 值最大，意味着在保证 的条件下， 可以取得极小值，也就是误差函数取得极小值，于是，最小化误差函数将使我们得到一个最大间隔的决策边界。事实上， 取得极小值将使得 ，并且图 4.3 虚线上的点都满足 ，这些点我们称之为“支持向量”（support vectors）！

异常值处理

我们现在对 已经有了更多的了解， 的目的是尽可能区分正负类样本，并且一旦能完全正确地分割样本它就“满足”了，因此对于线性可分的数据样本，通常它将得到无数条决策边界。同时优化 ，我们将从 得到的“候选边界”中选择一条“最佳边界”（最大间距的决策边界）。但是，假如 对所有“候选边界”都不满意怎么办？

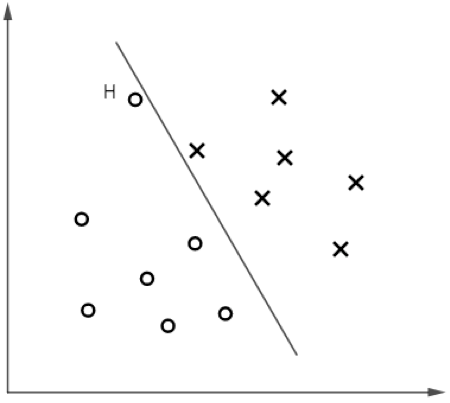
考虑图 5 的样本分布，如果我们再次忽略 ，仅让 取得极小值，得到的“候选边界”将位于一个狭窄的区域，图 5 显示了其中一条。

▲ 图5

图 5 中的 H 点为异常值（outlier）。显然，我们希望决策边界可以尽可能抵御异常值的干扰，回到最优的位置。事实上， 的加入将有效处理异常值问题，我们看它是怎么做到的。

假设 H 点为样本 ， 表示为：

图 6.1 的决策边界将使 ，即 取极小值，但是由于最小距离 非常小，最小化整体误差将使得 很大，即 增大；反之，图 6.2 的决策边界则使得 减小，从而 减小，与此同时， 增大将使得 增大。因此，同时优化 将得到一条介于两者之间的决策边界。一种具体的情况是，如果样本很多，那么 对 的影响很小，异常值将几乎被忽略，这正是我们希望的结果。

上述 对异常值处理的“效果”，我们通常称之为“正则化”（regularization），它可以避免模型“过拟合”（overfitting），相对的概念还有“欠拟合”（underfitting），后续文章将继续探讨。

现在我们可以说明常数 C 的作用，让我们再看一眼完整的误差函数：

假设 C 取一个很大的值，比如 1000000，则后半部分 产生的影响将很小（或者说 ) 的影响很大），于是也就无法起到正则化的作用，会导致过拟合；反之 C 取值很小，则容易欠拟合。

此外，带有正则化项（即 ）的 ，我们通常称之为目标函数（objective function）而不是误差函数（loss function），并且更通用的符号表示是 ，不过本文暂时采用误差函数的表达。

非线性SVM

考虑以下正负类样本，如何找到决策边界？

▲ 图7

我们目前所了解的 SVM 只能拟合线性边界，非线性边界需要对模型做一些“改装”。

具体操作非常简单。假设样本特征数量为 n，数据样本数量为 m，对于任意特定的数据样本 ，可以得到 与所有数据样本 的“相似度”（similarity）：

也就是说，对于每一个样本 （n 维），我们都可以得到相应的 （m 维）。

即为核函数（kernel function），通常我们采用高斯核（Gaussian kernel）：

对于不采用核函数的 SVM，我们通常说它用了线性核（linear kernel）。

通过将 替换为 ，我们可以得到核函数版本的 SVM 模型和误差函数：

关于极值点求解及核函数

为了说明极值点求解及核函数的原理，我们需要做一些看起来有些吓人的数学推导，由于篇幅有限，我将对一些关键的数学原理做简要说明，更详细的推导可参考斯坦福 CS 课程的资料 CS229 Lecture Notes. Andrew Ng. Spring Stanford University. 2020。

之前我们得到了一个优化问题：

其中：

容易得到，上述优化问题等价于：

注意到，我们还没有考虑正则化，比如图 6.2 所示的边界是不被允许的，因为 H 点不满足 的约束条件（ 而 ）。

因此，考虑到正则化和非线性可分的情况，我们将优化问题调整为：

现在你可以验证，假设 H 点对应  ，对于合适的  ，图 6.2 所示的边界将被允许，但是 H 点将带来 （类比 ）的误差值提升作为“惩罚”。事实上，上述优化问题等价于优化 SVM 的误差函数 。

以上为带约束的优化问题（constrained optimization problems）。其中一个解决思路是，找到优化问题 D，使得由 D 得到的解，可以得到原问题 P 的解。P 和 D 分别称为 primal problem 和 dual problem（以下翻译为原始问题和对偶问题）。关于 Duality 的严格定义，请参考 Duality(optimization). Wikipedia。

通常我们使用拉格朗日对偶（Lagrange duality）来求解。

对于一般化的带约束的优化问题 ，

求解步骤如下：

1. 找到该优化问题的替代问题 （跟 有相同的解）；
2. 得到对偶问题 ；
3. 求解 得到 的解。

定义拉格朗日函数如下：

考虑以下函数：

给定一个 值，如果 满足约束 ，可以得到：

如果 不满足约束，可以得到 （读者可自行验证）。

即：

因此我们得到以下优化问题 ：

容易验证 与 有相同的解。

进一步，得到对偶问题 ：

注意到，对偶问题的约束仅有 ，且 ，因此更容易求解。

可以证明：

以下用一个简单的例子说明上述不等式。假如 在 上处处连续，，。固定 ，则对于任意 ，都有 ，即 ；固定 ，则对于任意 ，都有 ，即 ，因此，。在满足一定条件下， ，比如马鞍形函数。

现在我们的目标是找到 使得 ，而 是否存在涉及两个条件：Slater's condition 和 Karush–Kuhn–Tucker conditions（以下简称斯莱特条件和 KTT 条件）。

斯莱特条件。对于以下优化问题：

当 和 为凸函数（convex），并且存在 使得：

则其满足强对偶性（strong duality）。

满足强对偶性的优化问题，其原始问题和对偶问题的最优解对应的目标函数值相等，即 。

对于如 所示形式的优化问题，KTT 条件如下：

对于 所示形式的优化问题，如果其满足强对偶性（比如满足斯莱特条件），以及相应的拉格朗日函数 关于 为严格凸函数，那么可以证明：

(1) 如果存在 是对偶问题的解，则 是原始问题的解；

(2) 和 分别为原始问题和对偶问题的解 满足 KTT 条件。

结论（1）告诉我们，可以通过求解对偶问题得到原始问题的解。结论（2）则提供了极值点的判断依据。注意到 KKT 条件（2），它意味着当 时， ，这将让 SVM 的优化结果得到少数的“支持向量”，下文将进一步说明。

我们可以对结论（1）作简单证明。

对于满足强对偶性的问题，令 和 分别为原始问题和对偶问题的解，可以得到：

即：

也就是说， 是 的极小值点，如果 是严格凸函数，则极小值点是唯一的。

以上，容易得到结论（1）。

现在，回到 SVM 的优化问题：

把上述约束条件转化为 的形式，注意到该优化问题有 2m 个 的约束，并且没有 的约束，我们可以得到拉格朗日函数：

于是，得到对偶问题：

对于 ，我们需要固定 ，令偏导数为零：

由以上方程可以得到 关于 的表达式，代入 ，可以得到对偶问题的最终表达式：

其中， 表示内积。求解上述问题可以采用基于梯度的迭代算法，并用 KTT 条件判断目标函数值是否收敛。SMO 是目前比较流行且高效的 SVM 优化算法，详情请参阅 SMO 的论文 Sequential Minimal Optimization: A Fast Algorithm for Training Support Vector Machines. John C. Platt. Microsoft Research. 1998。

现在，假设我们得到了对偶问题的极值点 ，在推导对偶问题表达式的过程，注意到：

可以得到决策边界的另一种表达式：

事实上，最终得到的 只有一小部分非零，这些非零的 对应的 就是支持向量。因此，我们的预测模型只需要计算 与少数支持向量的内积。

核函数

假如我们需要对样本进行特征组合，得到更高维的样本，比如进行如下特征映射：

注意到前文得到的对偶优化问题和预测模型都可以表示为 的函数，我们只需将 替换为 。一般地， 为特征映射，我们定义核函数为：

以特征数量 n=3 为例，考虑以下核函数：

可以看到上述核函数隐性地把 ,映射到高维向量 ，因此我们无需分别计算 ，这将减小计算复杂度，比如上述例子从 减小为 。

一个常用的核函数是：

我们称之为 RBF 核（Radial basis function kernel）或高斯核（Gaussian kernel）。通过泰勒展开可以得到 σ=1 的 RBF：

可以看到 RBF 实际上将 x 映射到无限维空间。

从另一个角度看待核函数。容易发现，RBF 的取值跟 的距离成负相关，值域为 ，当 时取最大值 ，因此 RBF 也可以视为 的相似度（similarity）表示。

关于 的作用。从相似度的角度理解核函数的作用，可以发现我们实际上通过计算输入 与所有训练样本的相似度来确定它的所属分类，最终我们会发现只需用到其中的部分训练样本就可以判断 的分类，这是支持向量的另一个理解角度。 是高斯函数的标准差，它决定了训练样本的影响范围，比如当 很小时，由于影响范围极小，导致我们几乎需要用所有训练样本来确定 的分类，因此得到的支持向量的数量会很大。因此，太小的 值会导致过拟合，太大会导致欠拟合。

在一些机器学习的工具库中，RBF 通常表示为：

即 ，因此有：

大的 或小的 ，容易导致过拟合，即低偏差、高方差；小的 或大的 ，容易导致欠拟合，即高偏差、低方差。

参考文献

[1] CS229 Lecture Notes. Andrew Ng. Stanford University. Spring 2020.

[2] Karush-Kuhn-Tucker conditions. Geoff Gordon. CMU. 

[3] Sequential Minimal Optimization: A Fast Algorithm for Training Support Vector Machines. John C. Platt. Microsoft Research. 1998.

[4] The Simplified SMO Algorithm. Stanford University. 2009.

[5]Duality(optimization). Wikipedia. 

[6] Hyperplane. Wikipedia. 

[7] Karush–Kuhn–Tucker conditions. Wikipedia. 

[8] Support Vector Machine. Wikipedia 

[9] Lagrange multiplier, Wikipedia. 

[10] Radial basis function kernel. Wikipedia. 

[11] Slater's condition. Wikipedia 

更多阅读

#投 稿 通 道#

 让你的论文被更多人看到 

如何才能让更多的优质内容以更短路径到达读者群体，缩短读者寻找优质内容的成本呢？答案就是：你不认识的人。

总有一些你不认识的人，知道你想知道的东西。PaperWeekly 或许可以成为一座桥梁，促使不同背景、不同方向的学者和学术灵感相互碰撞，迸发出更多的可能性。 

PaperWeekly 鼓励高校实验室或个人，在我们的平台上分享各类优质内容，可以是最新论文解读，也可以是学习心得或技术干货。我们的目的只有一个，让知识真正流动起来。

📝 来稿标准：

• 稿件确系个人原创作品，来稿需注明作者个人信息（姓名+学校/工作单位+学历/职位+研究方向） 

• 如果文章并非首发，请在投稿时提醒并附上所有已发布链接 

• PaperWeekly 默认每篇文章都是首发，均会添加“原创”标志

📬 投稿邮箱：

• 投稿邮箱：hr@paperweekly.site 

• 所有文章配图，请单独在附件中发送 

• 请留下即时联系方式（微信或手机），以便我们在编辑发布时和作者沟通

🔍

现在，在「知乎」也能找到我们了

进入知乎首页搜索「PaperWeekly」

点击「关注」订阅我们的专栏吧

关于PaperWeekly

PaperWeekly 是一个推荐、解读、讨论、报道人工智能前沿论文成果的学术平台。如果你研究或从事 AI 领域，欢迎在公众号后台点击「交流群」，小助手将把你带入 PaperWeekly 的交流群里。