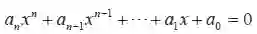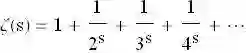无理数，超越数与级数

2018 年 6 月 25 日 算法与数学之美

无穷的直觉

人们无法设想整数列的尽头，只好试图宣称“数列是无穷的”。数列似乎是无穷的，但这是一种潜无穷。我们能描述得更精确一些吗？能否说出所有整数的数量，并计算它们？圣奥古斯丁认为，上帝且只有上帝才能做到：“神的智慧能够处理所有的无穷，不用心算就可以清点无数的生命。”继他之后经过了漫长的时期，人们“实现”了这种潜无穷：19 世纪，康托尔关于集合的理论和著作终于给无穷下了一个定义，或者说，定义了什么是“基数无穷”。

这时出现了另一个类似问题，与之前的问题略有不同。对于无论哪个数字，似乎总可以给出一个更大的整数，但人们想找到一个“比所有整数都大的数”。如果这个说法是有意义的，这个数只能是一个无穷数。这样一种无穷可以称为“序数无穷”，与上文提到的 “基数无穷”相对。

漫长的历史将数学家们引向了“序数无穷大”与“基数无穷大”，但数学中的无穷还有其他表现形式。我们将在第 3 章讲述无穷小和连续性的问题。在此之前，大家应当先认识到，一些有穷数字的运算需要借助无穷的概念，比如“无理数”问题，也就是不能表示成两个整数之比的数。

无理数

在公元前 6 世纪，受到毕达哥拉斯的影响，古希腊数学家们都认为，所有物理或几何的量都是一个整数或是整数的比值，称为“有理数”。很快，他们意识到自己需要用到一些不同于有理数的数。比如，我们可以用一个数与其自身相乘，得到它的平方；相反的运算可以得到平方根。但是，没有任何一个有理数是 2 的平方根；然而，边长为 1 的正方形的对角线正是这个值，记作 √2。同样，为了用栅栏圈起一块 2 平方千米大的正方形场地，你要准确计算场地的周长，计算结果是 4√2 千米，这也是个无理数。一个直角边为 1 米和 2 米的直角三角形的斜边长为√5 米，这也是个无理数。( √5-1)/2 的值被用来定义最美的人体比例。传统上，这是分割一段长度的最完美的比例，其定义方法是：较长部分与全长的比值等于较短部分与较长部分的比值——同样是个无理数。事实上，所有无理数与某一有理数进行加减乘除运算后得到的仍是无理数。

无理数的发现导致了数学史上第一次危机。其实，在实际应用中，无理数和整数、有理数一样必不可少。然而，无理数的定义、书写表达与无穷的概念有关：没有一个无理数能用有限的小数书写。

要写出一个无理数，需要将它的所有小数罗列出来。然而，这个数列的一个鲜明特点就是无穷性：如果数列是有穷的或是无限循环的，就证明这个无理数可以被写成两个整数的比，那么这就应当是一个有理数。无穷性的特点只体现在小数的书写中，但是它说明了一个事实：这些数字的确是一个无穷过程的结果。假设我们想确认两个无理数是否相等，那就必须将两个无理数的小数一位一位地比较——这将是一个无止境的工作。对无理数的所有运算得到的结果都是无理数。无理数既是有穷的也是无穷的，这取决于我们的思考角度：从长度角度来说，线段是有穷的；但从构成线段的点的数量角度来说，线段又是无穷的。

尽管无理数的定义涉及无穷，今天，我们对 √2 这样的数字仍可以随心所欲地进行运算。我们将这类数字定义为一列无穷的有理数极限，或者，如果我们愿意的话，还能将其定义为一个拥有无穷小数的数。构造无理数的无穷性彻底被掩盖，而对我们来说，这些数完全是有限的。

一些小数……

最简单的数字是正整数，如 1、2、3……用 N 来表示正整数集合。对正整数进行减法（与加法相对）运算可以得到负整数 -1、-2、-3……同样，除法（与乘法相对）运算可以得到分数或者有理数，用集合 Q 表示。所有有理数（也就是分数）可以写成小数的形式。但是，这些小数要么是有限的，比如 5/4 = 1.25，要么是无限循环的，比如 1/9 = 0.111111…是否可以设想一个无限但不循环的小数呢？答案是肯定的。它可以表示成分数吗？答案是否定的。这就是无理数。

超越数

在无理数中，还有一些数具有更复杂的特点——“超越数”，它们不能满足任一个

的整系数代数方程。

π 就是这样的数，它表示了圆的周长与直径之比；此外还有自然对数的底数 e = 2.71828…

莱布尼茨将微积分应用到解答物理学难题中，找到了超越曲线的解，也就是非代数方程的解。这些曲线就像超越数一样是无穷的，莱布尼茨说：“超越量的来源就是无穷。”从对超越曲线和无穷的研究来看，这些曲线作为某些物理计算的解，恰恰印证了一句话：“无穷在自然界中无处不在。”的确，数学中到处都有无穷的影子。否认无穷就得否认 π 和其他无理数：在圆中，在最短的一条线段中，在每个无理数中，都有无穷存在。

序列、级数与集合

序列主要存在于数学与物理学领域，也涉及无穷。以一个元素为基础定义下一个元素的过程，得出了一个序列。如果说，序列最基本的原型是整数数列，我们也可以有偶数数列、质数数列、立方体序列等。这个推导过程是没有终止的，所以序列是无穷的。序列的无穷特性带来的局限之一是，我们不能解决其中所有元素的所有问题。

我们能否将一个无穷序列视为一个完整的对象？至少某些确实可以。比如，我们已经看到每一个无理数都可以定义为某种有理数序列，称为“柯西序列”[1]。我们能像运算其他数一样运算无理数，这表示我们至少能运算某些无穷序列。[1] 我们也可以将一个无理数看作其小数的一个无穷序列。

一旦开始讨论序列，序列极限的问题就来了：序列如果存在极限，它便是一个数；我们在序列中越来越靠近这个极限。事实上，数学家定义了许多种“靠近”，而这又催生了一样多的集合与极限概念。如果存在这样一个极限，那么序列会收敛并趋向于这一极限。上文提到过的无理数可以被定义为某些有理数序列的极限。

数学家和物理学家总想计算一个序列中所有项的无限总和，于是会用到级数。项的数量是无限的，但计算结果可以是有限的；这样一来，级数就是“收敛的”，它给出了有限和无限的集合。要确定级数是收敛的并不容易；如果它是收敛的，计算它的值也很难。一个典型的例子是如下级数：S = 1/2 + 1/4 + 1/8 + … + 1/2^n，很难看出它是否是收敛的。然而，有一种“妙计”可以让我们计算它的值：构建表达式 S - 1/2 = 1/4 + 1/8 + … = 1/2（1/2 + 1/4 + …）= S/2；由于等式 S - 1/2 = S/2 成立，其值为解，即 S = 1。这并不表明这一级数是收敛的，但当我们证明了其收敛性后，便可以计算它的值。

所谓的调和级数，即 1 + 1/2 + 1/3 + 1/4 + …是发散的。莱昂纳多·欧拉给每一项乘 s 次幂后，给出了一个更广义的相似级数，称之为 ζ 函数（源于希腊字母 zeta）。这就有了

原始级数符合 s = 1，换句话说，第 n 项的值为 1/n^s。如果s ≤ 1，这个级数是发散的；如果 s ＞ 1，它就是收敛的。欧拉发现，级数的第一个意义是它与素数紧密相连。但数学家黎曼进一步思考，当 s 变成一个复数（不再是实数）时会发生什么，于是就有了黎曼 ζ 函数，根据不同的 s 值，级数或收敛或发散。重要的是，一种名为“解析延拓”的数学方法可以赋予级数一个值，即便它是发散的。

“黎曼假说”中的这些值被视为数学史上最重要的难题之一。

级数 1 + 1 + 1 + 1 + …自然是发散的，对应黎曼 ζ 函数值 s = 0；解析延拓此时为 -1/2。同样，1 + 2 + 3 + 4 + …明显也是发散的，对应黎曼 ζ 函数值 s = -1，也就是 -1/12。这样一来，解析延拓以一种惊人的方式赋予了发散级数一个有限值。这并不是把发散级数与有限值相联系的唯一方法，而欧拉（1707—1783）是最早考虑这种可能性的数学家之一。（未完待续）

作者 | [法]让-皮埃尔·卢米涅马克·拉雪茨-雷

来源 | 节选自《从无穷开始：科学的困惑与疆界》，人民邮电出版社，2018.4