深度研究自然梯度优化，从入门到放弃

会员服务 ·

深度研究自然梯度优化，从入门到放弃 | Deep Reading

2019 年 3 月 24 日 AI100

参加 2019 Python开发者日，请扫码咨询 ↑↑↑

作者 | Cold Marie Wild

译者 | 刘畅

责编 | Jane

出品 | AI科技大本营（公众号id：rgznai100）

【导语】根据自然梯度的支持者提出一种建议：我们不应该根据参数空间中的距离来定义值域空间，而是应该根据分布空间中的距离来定义它。这样真的有效？关于自然梯度优化，今天这篇文章值得大家一读！作者要以一个大家很少关注的角度讲一个肯定都听过的故事。

现在的深度学习模型都使用梯度下降法来进行训练。在梯度下降法的每个步骤中，参数值通常是从某个点开始，然后逐步将它们移动到模型最大损失减少的方向。我们通常可以通过从整个参数向量中计算损失的导数来实现这一点，也称为雅可比行列式。然而，这只是损失函数的一阶导数，它没有任何关于曲率的信息，换言之就是一阶导数改变的速度。由于该点可能位于一阶导数的局部近似区域中，并且它可能离极值点并不远（例如，在巨大的山峰之前的向下曲线），这时我们需要更加谨慎，并且不要以较大步长向下降低。因此，我们通常会采用下面等式中的步长 α 来控制我们的前馈速度。

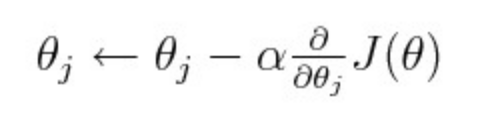
这个步长正在做这样一些事情：它以一个固定的值约束了你要在渐变方向上更新每个参数的距离。在这个算法的最简单版本中，我们采用一个标量，alpha，假设其值为 0.1，并将其乘以对损失函数求的梯度。注意，我们的梯度实际上是一个向量，也就是相对于模型中每个参数的损失梯度。因此当我们将它乘以标量时，实际上我们将沿着每个参数轴按照相同的固定量，按比例更新一个欧几里德参数距离。而且，在最基本的梯度下降版本中，我们在训练过程中使用的是相同步长。

但是......这样做真的有意义吗？使用较小学习率的前提是我们知道单个梯度的局部估计值可能仅在该估计周围的小局部区域中有效。但是，参数可以存在于不同的尺度上，并且可以对学习的条件分布产生不同程度的影响。而且，这种程度的影响可能会在训练过程中波动。从这个角度来看，在欧几里德参数空间中去固定一个全局范围看起来并不像是一件特别明智或有意义的事情

由自然梯度的支持者提出的另一种建议是，我们不应该根据参数空间中的距离来定义值域空间，而是应该根据分布空间中的距离来定义它。因此，不应该是“在符合当前梯度变化时，将参数向量保持在当前向量的 epsilon 距离内”，而应该是“在符合当前梯度变化时，要保持模型的分布是在之前预测分布的 epsilon 距离内”。这里的概念是两个分布之间的距离，而且对于任何缩放移位或一般的参数重置是具有不变性的。例如，可以使用方差参数或比例参数（1 /方差）来参数化相同的高斯分布；如果你查看参数空间，根据它们是使用方差还是比例进行参数化，两个分布将是不同的距离。但是如果你在原始概率空间中定义了一个距离，它就会是一致的。

接下来，本文将尝试建立一种更强大，更直观的理解方法，称为自然梯度学习，这是一种在概念上很优雅的想法，是为了纠正参数空间中尺度的任意性。我将深入探讨它是如何工作的，如何在不同数学思想之间构建起桥梁，并在最后讨论它是否以及在何处实际有用。

所以，第一个问题是：计算分布之间的距离有什么用？

KL散度赋能

KL散度，更确切地说是 Kullback-Leibler 散度，在技术上并不是两个分布之间的距离度量（数学家对于所谓的度量或合适的距离是非常挑剔的），但这是一个非常近似的想法。

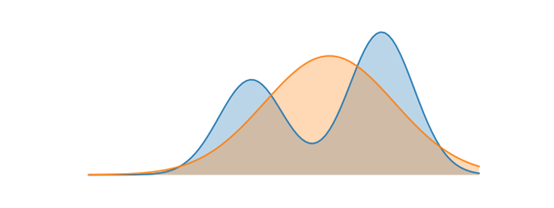
在数学上，它是通过计算从一个分布或另一个分布采样的 x 值取得的对数概率的比率的期望值（即，概率值的原始差异）来获得的。于是，取自其中一个分布或另一个分布的期望使得它成为了一个非对称度量，其中 KL（P || Q）！= KL（Q || P）。但是，在许多其他方面，KL 散度带给我们关于概率距离是这样的概念：它是直接根据概率密度函数的定义来衡量，也就是说，在定义的分布上的一堆点的密度值的差异。这有一个非常实用的地方，对于“X的概率是多少”这样的一个问题，当X没限定范围时，可以有各种不同的分布。

在自然梯度的背景下，KL散度是一种用来衡量我们模型预测的输出分布变化的方式。如果我们正在解决多分类问题，那么我们模型的输出将是可以看作多项分布的 softmax，每个类都有不同的概率。当我们谈论由当前参数值定义的条件概率函数时，也就是我们讨论的概率分布。如果我们采用 KL 散度作为缩放我们梯度步长的方式，这意味着对于给定的输入特征集，如果它们导致预测的类别分布在 KL 散度方面非常不同，那么我们在这个空间中看到的两个参数配置也会大相径庭。

相关的费舍尔理论

到目前为止，我们已经讨论过为什么在参数空间中缩放更新每一步的距离是令人不满意的，并给出了一个不那么随意的替代方案：也就是我们模型预测的类分布最多只能在一个 KL 散度范围内，去更新我们的每一步距离。对我来说，理解自然梯度最困难的部分是另一部分：KL 散度和 Fisher 信息矩阵之间的联系。

先讲故事的结尾，自然梯度是像下面公式这样实现的：

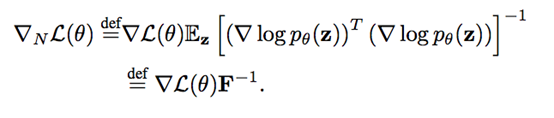
在等号上面的 def 意思是右边的内容是左边符号的定义。右边是由两部分组成，首先，是参数关于损失函数的梯度（这是与正常梯度下降步骤中使用的一样的梯度）。“自然”位来自第二个部分：Z 的对数概率函数的平方梯度的期望值。我们将这整个部分，称为 Fisher 信息矩阵，然后将损失梯度乘以其逆。

p-theta（z）项是由我们的模型定义的条件概率分布，也就是说：神经网络末端的 softmax。我们正在研究所有 p-theta 项的梯度，因为我们关心的是模型预测的类概率因参数变化而变化的量。预测概率的变化越大，我们参数更新前和更新后的预测分布之间的 KL 差异越大。

对自然梯度优化感到困扰的部分原因在于，当你正在阅读或思考它时，你必须理解两个不同的梯度对象，也就是两个不同的事物。顺便说一句，这对于想要深入了解它是不可避免的一步，特别是在讨论概率时。我们没有必要去抓住这样的一个直觉; 如果您不喜欢浏览所有的细节，请随时跳到下一部分

关于损失函数的梯度

通常，分类损失是一个交叉熵函数，但更广泛地说，它是一些函数，它将模型的预测概率分布和真实目标值作为输入，并且当模型的预测分布远离目标时，损失值就更高。这个对象的梯度是梯度下降学习的核心; 它表示如果将每个参数移动一个单位，损失值就会发生变化。

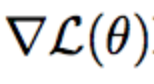
对数似然的梯度

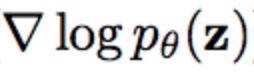
对于我来说，这是学习自然梯度最令人困惑的部分。因为，当您去阅读有关 Fisher 信息矩阵的内容，将获得许多说明它与模型的对数似然的梯度有关的内容。我之前对似然函数的理解是，它代表了你的模型在某些数据集上预测的正确可能性有多大，特别是，您需要目标值才能计算它，因为您的目标是计算模型预测出真实目标的概率。在讨论可能性的大多数情况下，例如非常常见的最大似然技术，您会关心对数似然的梯度，因为似然越高，模型从真实分布中采样的值的概率越高，当然我们就很乐意看到这样的结果。实际上，这看起来像计算 p（class | x）梯度的期望值，其中概率是在数据的实际类分布中得出。

但是，你也可以用另一种方式来估计似然值，而不是根据真实目标值计算您的似然（也就是采用非零梯度，因为它可能增加模型参数对目标预测准确的概率）。你可以使用从条件分布本身中提取的概率来计算期望。也就是说，如果网络是采用 softmax，而不是基于给定观察数据中的真实类别，以 0/1 概率取得 logp（z）的期望，那么使用该模型的估计概率作为其权重，将导致整体期望梯度值为 0，因为我们的模型是以当前的置信度作为基本事实，但我们仍然可以得到对梯度方差的估计（即梯度平方），也就是在 Fisher 矩阵中（隐含地）计算预测类空间中的 KL 散度时，需要用到的值。

所以......它有帮助吗？

这篇文章花了很多时间来谈论机制：究竟什么叫做自然梯度估计，以及关于它如何以及为什么能起作用的更好的一种直觉。但是，如果我不回答这个问题，我觉得自己会失职：这件事真的有价值吗？

简短的回答是：实际上，它并没有为大多数深度学习应用程序提供足够引人注目的价值。有证据表明自然梯度仅需要很少的步骤就能让模型收敛，但正如本文稍后将讨论的那样，这是一个复杂的比较过程。对于那些被参数空间中随意更新步骤的方法困扰的人来说，自然梯度的想法是优雅并且令人满意的。但是，除了优雅之外，我不清楚它是否提供了更多的价值。

据我所知，自然梯度提供了两个关键的价值来源：

1、它提供有关曲率的信息

2、它提供了一种直接控制模型在预测分布空间中移动的方法，而且与模型在损失空间中的移动是分开的

曲率

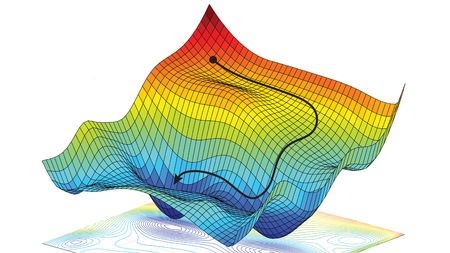
现有的梯度下降法的一大奇迹是它通过一阶求导完成。一阶方法是仅计算与要更新的参数相关的导数。使用一阶导数，您所知道的是曲线在特定点处的切线。您不知道切线的变化速度有多快。而二阶导数，会更具有描述性，即函数在任何给定方向上的曲率水平。要知道曲率是一个非常有用的东西，因为在高曲率区域，梯度从一点到另一点的急剧变化，所以优化时需要谨慎的迈出一大步，以免被正在攀登的陡峭山峰的局部信息误导，而跳下就在眼前的悬崖。我喜欢这样思考的方法，如果你处于一个点到点的梯度变化很大的地区（也就是说：高方差），那么你 minibatch估计的梯度在某种意义上就更加的不确定。相比之下，如果梯度在给定点几乎没有变化，那么下一步就不需要谨慎了。二阶导数信息非常有用，因为它可以根据曲率水平来缩放每一步的大小。

实际上，自然梯度是将参数更新除以梯度的二阶导数。梯度相对于给定参数方向变化越大，Fisher 信息矩阵中的值越高，那么在该方向上更新的步幅大小越低。这里讨论的梯度是批次中各点的经验似然的梯度。这与损失函数方面的梯度不同。但是，直观地说，似然的巨大变化与损失函数的剧烈变化并不相符。因此，通过捕获关于给定点处的对数似然导数空间的曲率的信息，自然梯度也给出了真实的损失空间中的曲率信息。有一个非常有力的论据，当自然梯度已被证明可以加速收敛（至少在所需梯度步幅的数量方面），这就是价值的来源。

然而请注意，本文提到自然梯度可以在梯度步骤方面加速收敛。这种精确度来自于自然梯度的每个单独步骤需要更长时间，因为它需要计算 Fisher 信息矩阵，记住，这是一个存在于 n_parameters² 空间中的数量。事实上，这种急剧放缓类似于通过计算真实损失函数的二阶导数引起的减速。虽然是这种情况，但我还没有看到计算自然梯度的 Fisher 矩阵能够比计算相关损失函数的二阶导数更快。以此为假设，与对损失函数本身进行直接二阶优化的（也可能是同样的代价高昂）方法相比，很难看出自然梯度提供的值域是多少。

现代神经网络能够在理论预测只有一阶导数失败的情况下取得成功的原因有很多，深度学习从业者已经找到了一堆巧妙的技巧来凭经验逼近二阶导数矩阵中所包含的信息。

Momentum 作为一种优化策略，它是通过保持上一次梯度值的加权平均值并将任何给定的梯度更新偏向该值移动的方向来起作用。这有助于解决在梯度值变化很大时的一部分问题：如果你经常得到相互矛盾的梯度更新，他们通常会取一个平均值，类似于减慢你的速度学习率。而且，相比之下，如果你反复得到相同方向的梯度估计值，那就表明这是一个低曲率区域，并会建议采用更大的步长，而 Momentum 正是遵循这一规律。

RMSProp，令人捧腹的是，它是由 Geoff Hinton 在课程中期发明的，它是对以前存在的称为 Adagrad 的算法的修改。RMSProp 通过获取过去平方梯度值的指数加权移动平均值，或者换句话说，过去的梯度方差，并将更新的步长除以该值。这可以大致被认为是梯度的二阶导数的经验估计。

Adam（自适应的矩估计方法），它基本上是结合了上述的两种方法，估计梯度的实际平均值和实际方差。它是当今最常见，也是最常用的优化策略之一，主要是因为它具有平滑掉嘈杂的一阶梯度信号的效果。

还值得一提的是，以上这些方法除了通常根据函数曲率缩放更新步长之外，它们还能根据这些特定方向上的曲率值不同地缩放不同的更新方向。这与我们之前讨论的内容有点类似，也就是按相同的数量缩放所有参数可能不是一件明智的事情。您甚至可以根据距离来考虑这一点：如果某方向上的曲率很高，那么在欧几里德参数空间中相同数量的步长将使我们在梯度值的移动上比预期的更远。

因此，虽然在定义参数更新的连贯方向方面不具备自然梯度的优雅，但它确实能够在曲率不同的地方，准时的调整方向和更新步长。

根据分布直接决定

OK，最后一节论述的是：既然直接分析 N² 的计算似乎都是非常耗时的，如果我们的目标是使用对数似然的分析曲率估计去替代损失曲率估计，为什么我们不直接采用后者，或接近后者的方式。但是，如果您处于这样一种情况，即您实际上是在关注预测类别分布的变化，而不仅仅是损失变化？这种情况甚至会是什么样的？

这种情况的一个例子，是当前自然梯度方法的主要领域之一：强化学习领域的信任区域策略优化（Trust Region Policy Optimization, TRPO）。在策略梯度的设置中，您在模型结束时预测的分布是以某些输入状态为条件的动作分布。而且，如果您正在从您模型当前预测的策略中收集下一轮训练的数据训练来学习 on-policy，则有可能将您的策略更新为一个死循环。这就是策略遭受灾难性打击的意义所在。为了避免这种情况，我们要谨慎行事，而不是做可以显著改变我们策略的梯度更新。如果我们在预测概率发生变化的过程中保持谨慎，那就极少会出现死循环的情况。

这就是自然梯度的一个案例：在这里，我们关心的实际上是在新参数配置下不同行为的预测概率变化了多少。我们关心的是模型本身，而不仅仅是损失函数的变化。

最后，我想通过两个我仍然存在的困惑来结束这篇文章

1、我不敢确定计算对数似然的 Fisher 矩阵是否比仅仅计算损失函数的 Hessian 更有效（如果是，那将是自然梯度获得关于损失曲面曲率信息的更容易的方式）

2、我比较不相信，当我们在 z 的对数概率上计算期望时，那个期望值能够替代我们模型预测的概率（期望必须相对于某些概率集来定义）。

--【完】--

（本文为 AI科技大本营编译文章，转载请微信联系 1092722531）

敲黑板划重点！7 折优惠限时抢购中，3 月 31 日前可享受优惠价 499 元，欢迎点击阅读原文报名参加。更多详细信息请咨询13581782348（微信同号）。