你的模型真的陷入局部最优点了吗？

小夕曾经收到过一个提问：“小夕，我的模型总是在前几次迭代后很快收敛了，陷入到了一个局部最优点，怎么也跳不出来，怎么办？”

 

本文不是单纯对这个问题的回答，不是罗列工程tricks，而是希望从理论层面上对产生类似疑问的人有所启发。

真的结束于最优点吗？

 

我们知道，在局部最优点附近，各个维度的导数都接近0，而我们训练模型最常用的梯度下降法又是基于导数与步长的乘积去更新模型参数的，因此一旦陷入了局部最优点，就像掉进了一口井，你是无法直着跳出去的，你只有连续不间断的依托四周的井壁努力向上爬才有可能爬出去。更何况梯度下降法的每一步对梯度正确的估计都在试图让你坠入井底，因此势必要对梯度“估计错很多次”才可能侥幸逃出去。那么从数学上看，什么才是局部最优点呢？

 

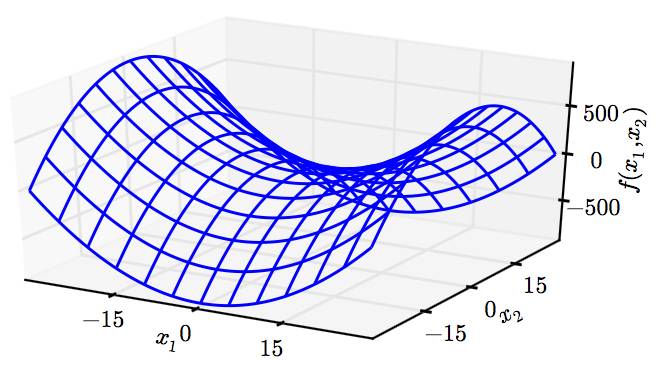
这个问题看似很白痴，很多人会说“局部最优点不就是在loss曲面上某个一阶导数为0的点嘛”。这就不准确啦，比如下面这个马鞍形状的中间的那个点：

（图片来自《deep learning》）

 

显然这个点也是（一阶）导数为0，但是肯定不是最优点。事实上，这个点就是我们常说的鞍点。

 

显然，只用一阶导数是难以区分最优点和鞍点的。

我们想一下，最优点和鞍点的区别不就在于其在各个维度是否都是最低点嘛～只要某个一阶导数为0的点在某个维度上是最高点而不是最低点，那它就是鞍点。而区分最高点和最低点当然就是用二阶导数（斜率从负变正的过程当然就是“下凸”，即斜率的导数大于0，即二阶导数大于0。反之则为“上凹”，二阶导数小于0）。也就是说，若某个一阶导数为0的点在至少一个方向上的二阶导数小于0，那它就是鞍点啦。

那么二阶导数大于0和小于0的概率各是多少呢？由于我们并没有先验知识，因此按照最大熵原理，我们认为二阶导数大于和小于0的概率均为0.5！

 

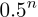
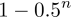
那么对于一个有n个参数的机器学习/深度学习模型，“loss曲面”即位于n+1维空间（loss值为纵轴，n个参数为n个横轴）。在这个空间里，如果我们通过梯度下降法一路下滑终于滑到了一个各方向导数均为0的点，那么它为局部最优点的概率即，为鞍点的概率为，显然，当模型参数稍微一多，即n稍微一大，就会发现这个点为鞍点的概率会远大于局部最优点！

好吧我再啰嗦的举个栗子，已经反应过来的同学可以跳过这个栗子：

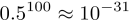
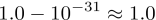
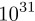
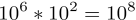
假设我们的模型有100个参数（实际深度学习模型中一般会远大于100），那么某一阶导数为0的点为局部最优点的概率为约为，而为鞍点的概率则为。就算我们的模型在训练时使用了特别厉害的“超级梯度下降法”，它可以每走一步都恰好踩在一个一阶导数为0的点上，那么从数学期望上来看，我们需要走步才行。而实际的projects中，哪怕数据集规模为千万级，我们分了100万个batches，然后要迭代100次，那也仅仅是走了步，你真的觉得运气可以辣么好的走到局部最优点上去吗？所以实际中，当我们的深度学习模型收敛时，几乎没有必要认为它收敛到了一个局部最优点，这完全等同于杞人忧天。

 

也就是说，如果最后模型确实在梯度下降法的指引下收敛到了一个导数为0的点，那这个点几乎可以肯定就是一个鞍点。

 

如果我们的模型真的收敛到鞍点上了，会很可怕吗？

 

这就又回到了文章开头的那副马鞍状的图。

显然，站在马鞍中央的时候，虽然很难翻过两边的山坡，但是往前或者往后随便走一步就能摔下马鞍！而在文章《batch size》中小夕讲过，我们默认使用的mini-batch梯度下降法本身就是有噪声的梯度估计，哪怕我们位于梯度为0的点，也经常在某个mini-batch下的估计把它估计偏了，导致往前或者往后挪了一步摔下马鞍，也就是mini-batch的梯度下降法使得模型很容易逃离特征空间中的鞍点。

 

那么问题来了，既然局部最优点很难踩到，鞍点也很容易逃离出去，那么为什么我们的模型看起来是收敛了呢？

 

初学者可能会说 “诶诶，会不会是学习率太大了，导致在“鞍点”附近震荡？” 首先，鞍点不像最优点那样容易震荡，而且哪怕你不断的减小学习率继续让模型收敛，你这时计算output层或者后几层的梯度向量的长度时会发现它依然离0很遥远！（这句话是有实验支撑的，不过那篇论文我找不到惹，也忘了名字了。热心的观众帮忙补充一下哦）

 

难道，踩到的鞍点太多，最后恰好收敛到一个跳不下去的鞍点身上了？

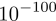
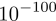
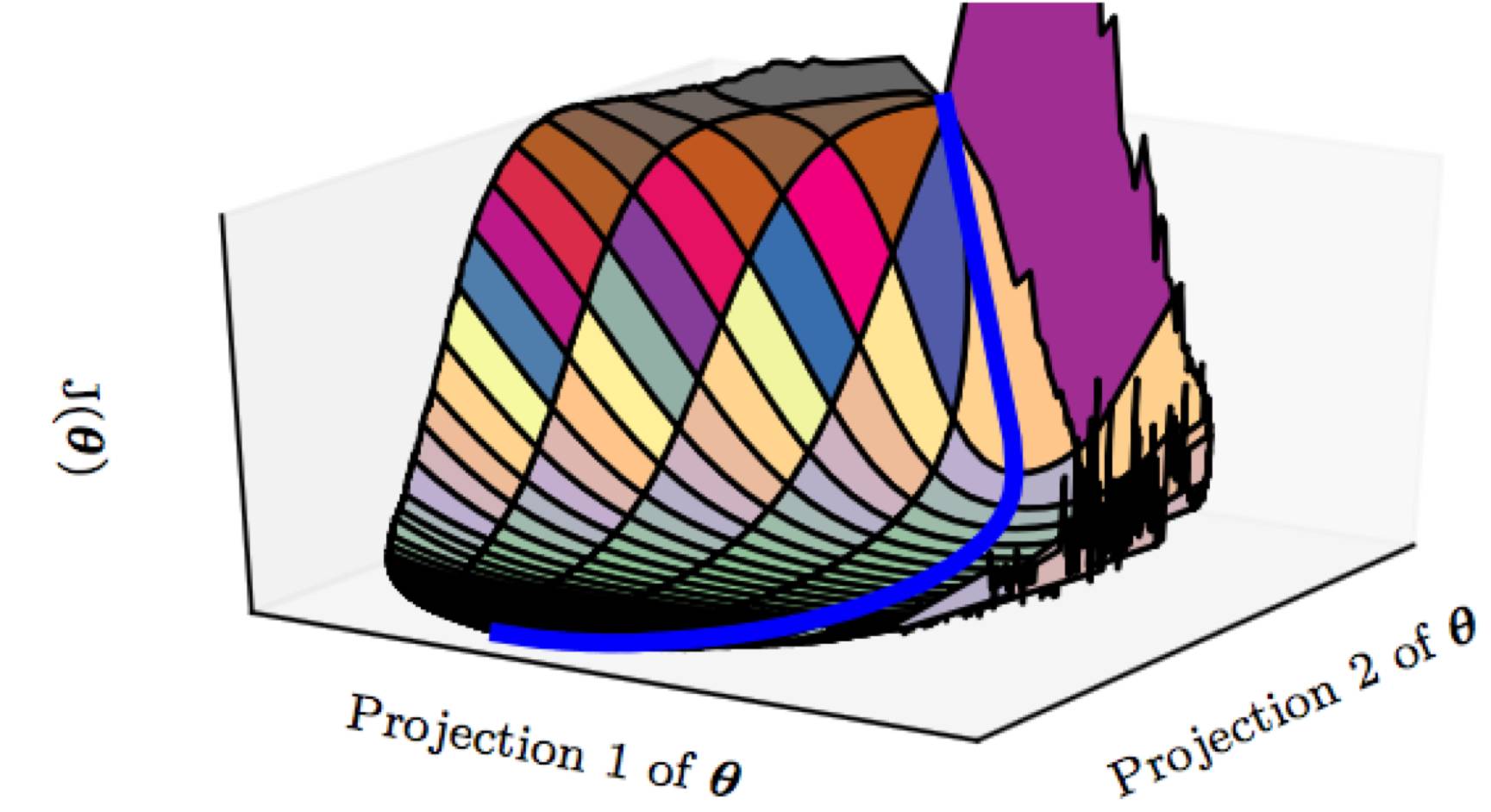
虽然高维空间中的鞍点数量远远大于最优点，但是鞍点的数量在整个空间中又是微不足道的：按前面的假设，假设在某个维度上随机一跳有10%的概率踩到导数为0的点，那么我们在101维的空间中的一步恰好踩到这个点上的概率为，也就是说在101维空间里随机乱跳的时候，有的可能性踩到鞍点身上。因此，即使有难以逃离的鞍点，那么被我们正好踩到的概率也是非常小的。

 

所以更令人信服的是，在高维空间里（深度学习问题上）真正可怕的不是局部最优也不是鞍点问题，而是一些特殊地形。比如大面积的平坦区域：

 

（图片来自《deep learning》）

 

在平坦区域，虽然导数不为0但是却不大。虽然是在不断下降但是路程却非常长。对于优化算法来说，它需要走很多很多步才有可能走过这一片平坦区域。甚至在这段地形的二阶导数过于特殊的情况下，一阶优化算法走无穷多步也走不出去（设想一下，如果终点在一米外，但是你第一次走0.5米，后续每一步都是前一步的一半长度，那么你永远也走不到面前的一米终点处）。

所以相比于栽到最优点和鞍点上，优化算法更有可能载到这种类似平坦区的地形中（如果这个平坦区又是“高原地带”，即loss值很高的地带，那么恭喜你悲剧了）。更糟糕的是，由于高维地形难以可视化，还有很多更复杂的未知地形会导致假收敛，一旦陷入到这些危险地形中，几乎是无解的。

 

所以说，在深度学习中，与其担忧模型陷入局部最优点怎么跳出来，更不如去好好考虑：

1. 如何去设计一个尽量没有“平坦区”等危险地形的loss空间，即着手于loss函数的设计以及深度学习模型的设计；

2. 尽量让模型的初始化点远离空间中的危险地带，让最优化游戏开始于简单模式，即着手于模型参数的初始化策略；

3. 让最优化过程更智能一点，该加速冲时加速冲，该大胆跳跃时就大胆跳，该慢慢踱步时慢慢走，对危险地形有一定的判断力，如梯度截断策略；

4. 开外挂，本来下一步要走向死亡的，结果被外挂给拽回了安全区，如batch normalization策略等。