《博弈论与美海军预算》2023最新52页论文

这是资本预算和随机组合优化中基于风险的决策分析的第二阶段后续工作。研究目的是提出一种新颖、可重复使用和可扩展的高级分析流程，采用战略博弈论和综合风险管理（IRM），协助美国防部在不确定情况下开展资本预算编制活动，并应用于蒙特卡罗风险模拟、预测和预测分析，以及具有多个利益相关者的收购和项目组合的随机组合优化（约束条件包括预算、进度、成本、风险和其他战略约束条件）。博弈论应用将包括具有战略和扩展形式的完全和不完全信息的重复有限和无限博弈领域。研究方法将酌情包括理论数学公式、建议的数据收集/整合和优化方法，以及实际实施建议，以测试建议方法的益处和可行性，从而根据其他国家或内部参与者（如美国国会、国防部内部组织）的反应生成最佳预算分配和战略。在适当情况下，将采用战略和扩展形式。博弈论的假设包括决策者的理性和使用贝叶斯定律的最新信息。我们的想法是分析在重复博弈中具有支配和被支配条件的纯策略和混合策略的伯特兰、库诺和纳什均衡，以确定推荐的方法。我们利用军事主题专家来确定参与连续和同时移动的概率报酬结构，以确定主博弈树中的均衡状态，从而确定子博弈完全纳什均衡，作为该方法的工作实例和说明。可交付成果包括书面报告、Excel 文件和研究中生成的相关脚本。

项目总结

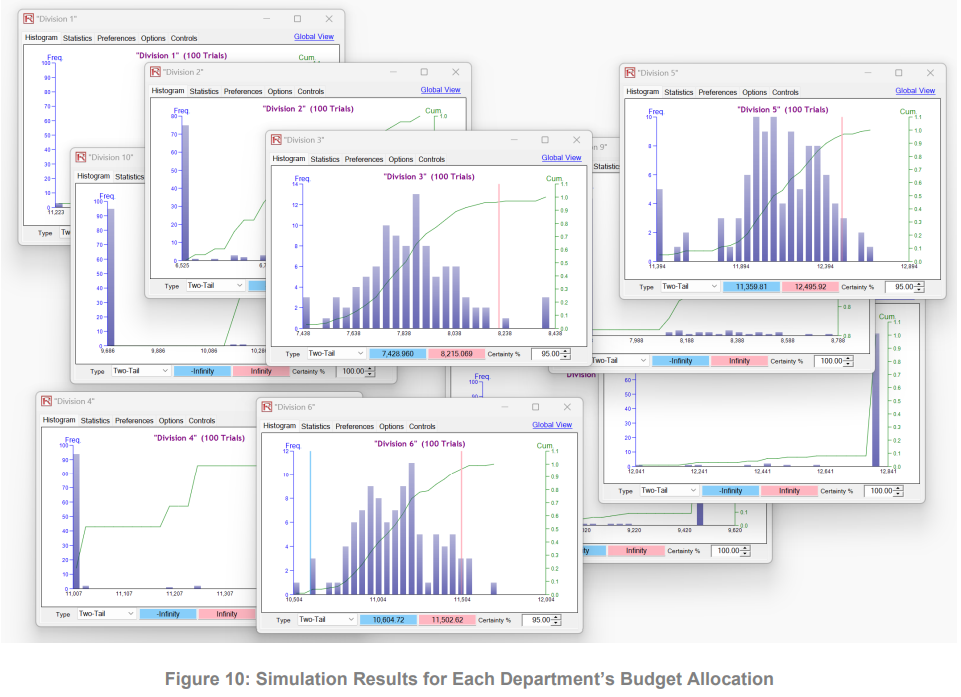
海军内部的许多机构都在争夺海军预算的一部分，以确保本机构获得尽可能多的预算。由于 24 财年的预算高达 2558 亿美元，美国海军必须尽一切可能做出最明智的决定。考虑到一个部门下设多个部门，这些部门将从该部门获得资金。本研究中应用的机械设计理论使我们能够创建一个博弈，其所需的纳什均衡是各部门准确预测预算。我们创建了一个博弈序列，对超出特定容差范围的不准确预算预测进行惩罚，并对准确预测预算的部门进行奖励。为了展示将博弈序列与传统预算分配理念相结合的方法，我们使用了仿真技术来模拟博弈序列中的实际决策。这些模拟的输出结果为每个分部提供了总预算分配部分的置信区间。利用军事价值和军事弊端的附加指标，在博弈序列模拟的置信区间内对预算进行随机优化，从而得出最终的预算分配结果。

推荐的方法和手段可以独立运行，也可以与综合风险管理方法结合使用，在综合风险管理方法中，蒙特卡罗模拟、预测预报和随机组合优化可以整合在一起，从而创造出一种更稳健、更全面的方法。研究得出结论，纳入博弈论可以提高各部门报告内容的稳健性，因为目标是可以实现的。该方法迫使各部门报告其最佳估计，并自我调节各部门，以逐步改善其预测。

研究背景

当前的研究在美国防部内使用博弈论结构和基于风险的随机资本预算程序，采用了几种独特的方法来提高其性能，以产生可信且合理的博弈论随机投资组合分配。相关性的关键点在于，该研究有助于为高级决策者提供有关最佳项目选择和资源组合分配的见解、方向和可操作的情报。成功的标准将是在不确定的情况下确定一个站得住脚的投资组合分配，并从多个角度和方法运用博弈论概念来三角测量一个有效和可靠的军事价值。这些技术可用于选择可能性的相关组合，利用马科维茨的有效前沿并在博弈论方法的框架内进行随机优化。这可以通过先前研究项目中的各种组合和计划选择技术得到进一步加强，以衡量它们与博弈论的配合程度，这些技术包括用于充实评估的偏好排序组织方法（PROMETHEE）、表达现实的消除和选择（ELECTRE）、多标准分析（MCA）和分层评分-排序（HSR）方法。

这项研究将综合风险管理（基于风险的蒙特卡罗模拟、预测和预测建模）和随机优化（涉及多个利益相关者，有预算、进度、成本、风险和其他战略约束）等各种方法与博弈论概念结合起来。具体来说，诺贝尔奖获奖方法涉及讨价还价中的信息不对称问题，将应用机制设计理论和启示原则，从纳什均衡开始，然后将其修改为博弈，旨在激发项目经理的诚实预测，从而在国防部内实现高效和有效的预算分配。

这项研究是资本预算和随机组合优化中基于风险的决策分析的第二阶段后续工作。研究目的是提出一种新颖、可重复使用和可扩展的高级分析流程，采用战略博弈论和综合风险管理，协助国防部在不确定情况下开展资本预算编制活动。博弈论应用将包括具有战略和扩展形式的完全和不完全信息的重复有限和无限博弈领域。研究方法包括理论数学公式、建议的数据收集和整合、优化方法以及实际实施建议，以测试建议方法的益处和可行性，从而根据其他参与者（国防部内的不同部门或组织）的反应生成最佳预算分配和战略。博弈论的假设条件包括决策者的理性和使用贝叶斯定律的最新信息。为了确定推荐的方法，我们的想法是分析重复博弈中具有支配和被支配条件的纯策略和混合策略的伯特兰、库诺和纳什均衡。我们使用模拟并确定连续和同时移动的报酬结构，以确定主博弈树中的均衡状态到子博弈完美纳什均衡，作为该方法的工作实例和说明。

研究结果和结论

根据研究结果，主要发现表明，所建议的博弈论方法需要是一种平衡的方法，并且要切实可行，以便决策者能够轻松理解。因此，建议的模型和方法符合许多理想的特性。建议的方法符合现代经济理论，模型符合现代机制设计理论和启示原则，这在减少信息不对称问题方面是最先进的。在实践中，该模型简单、直观、切实可行。建议的模型和方法只有几个参数，解释简单实用。在协商预算（第一年，第一轮）后，项目经理只需如实估计一个参数（η）。奖励真实的模型是直观的，看起来很有吸引力。

在研究意义方面，发现所提出的模型和方法具有应用灵活性，该模型可灵活地适应总部的偏好和具体条件。该模型在惩罚程度上具有灵活性，惩罚程度可以是对称的（λ1 和 λ2），允许预测误差的容忍度，并为诚实报告增加额外的溢价。最后，还要考虑动态效应，即随着时间的推移，该方法将揭示哪些是高生产率的项目经理，哪些是低生产率的项目经理。对于低生产率的计划管理人员，除了更换他们之外，还可以在某一年后稍微改变游戏规则，以激励他们克服自身的局限性。对于高生产率的计划管理人员，则需要反其道而行之：始终明确未来参数控制的选择权将属于他们而非总部，从而防止棘轮效应。

本文建议，在实施预算分配时，如果各部门或分部之间存在激烈竞争，而且正在实施的计划的结果存在足够的不确定性，那么就应该考虑博弈论。博弈论有助于减少未来的不确定性，使各部门对其计划的产出预测负责。通过让各部门承担责任，滚动组合就更有可能实现预期目标。