金融时间序列预测中的可解释人工智能（XAI）综述

人工智能（AI）模型已经达到了非常显著的准确性。尽管其优越的性能带来了巨大的好处，但其内在的复杂性往往降低了人类的信任，从而减缓了它们在高风险决策领域（如金融领域）的应用。可解释人工智能（XAI）领域旨在弥合这一差距，旨在使AI模型更易于理解。本综述重点关注过去五年发表的工作，对预测金融时间序列的XAI方法进行了分类。在本文中，可解释性和可理解性被区分开来，强调了需要分别对待这些概念，因为它们在实践中的应用方式不同。通过清晰的定义、严格的XAI方法分类、互补的特征描述以及XAI在金融行业应用的实例，本文全面展示了XAI在当前金融中的角色。它还可以作为选择最合适的XAI方法进行未来应用的指南。

引言

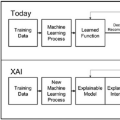
在过去的十年中，人工智能（AI）在准确性方面取得了显著进展，变革了商业、媒体、医疗、教育、金融、科学研究、司法等多个领域。尽管这些进步提供了前所未有的能力，但它们也在高风险、敏感领域如金融和医疗保健中引入了挑战。尽管AI模型的准确性很高，但由于其黑箱性质，用户信任度往往较低。伦理和法律框架已经演变以反映这些担忧；如[68]和[82]所指出的报告强调了在决策情境中理解AI系统的必要性。现有研究[10, 63, 68]指出，深度学习模型的可解释性差会显著增加投资风险，从而对实际应用造成重要限制。 为解决这一问题，新兴的可解释人工智能（XAI）领域致力于开发不仅准确而且对人类用户可理解的AI模型。XAI提供了两条主要途径来增强理解：可解释模型，它们本身就是可以理解的，以及需要额外方法进行解释的解释模型。然而，文献中存在显著的术语混淆；可解释和可解释的术语常被互换使用，导致对所呈现模型本质的误解。理解这些术语之间的差异至关重要，原因有几个。首先，实现可解释性和可解释性的途径不同，需采用不同的方法和评估。其次，准确的术语有助于根据金融应用的独特监管和伦理需求选择合适的模型。第三，清晰的定义改善了数据科学家、金融专家和政策制定者之间的跨学科沟通，促进更明智的决策。第四，区分可解释性和可解释性影响了对模型决策过程信任度的评估，从而影响风险评估和金融法规的合规性。此外，声称模型为XAI有时缺乏实质性支持，要么未能展示对模型的解释，要么缺乏帮助理解模型的解释。 金融行业加速采用AI用于复杂任务，如信用风险评估、欺诈检测、算法交易以及金融时间序列预测，这进一步突显了本综述的必要性。尽管这些技术有望提高效率和准确性，但它们也引发了关于公平性、可解释性和监管合规性的重大担忧。AI算法的黑箱性质不仅是技术挑战；它对公众信任、伦理治理和监管遵从有深远影响。本文旨在介绍用于金融时间序列预测的最新可解释模型和解释方法。通过提供可解释和解释模型的详细综述，本文旨在为两个读者群体服务：希望设计和开发XAI用于时间序列预测（无论是金融的还是其他领域）的数据科学家，以及希望将XAI整合到其分析环境中以预测金融时间序列的金融专业人士。事实上，本文综述的用于预测金融时间序列的可解释和解释方法也可用于预测多种类型的时间序列。此外，本综述提供了XAI所实现的金融见解，这些见解和方法对于金融专业人士同样有用。此外，本综述为持续研究提供了严格的基础，指导从业者选择最合适的方法，并让他们了解各种方法的优缺点。总之，本综述旨在促进AI在金融中的负责任和透明应用，将最前沿的机器学习技术与该行业严格的伦理和监管标准相结合。据我们所知，这是首个专注于预测金融时间序列的XAI综述。 本文对过去五年中用于预测金融时间序列或预测金融时间序列变化的XAI模型进行了分类。首先，在第二部分中定义了一些重要概念。其次，介绍了本综述的方法论及由分类法得出的图表（第三和第四部分）。第三，介绍并根据XAI原则分类了可解释模型和解释方法（第五和第六部分）。在第七部分，根据社区已知的解释特征[6, 27, 49]对相同的方法进行了不同标准的描述。然后，介绍了XAI在行业中的应用（第八部分）。最后，提出结论及有待完成的工作（第九部分）。

分类法

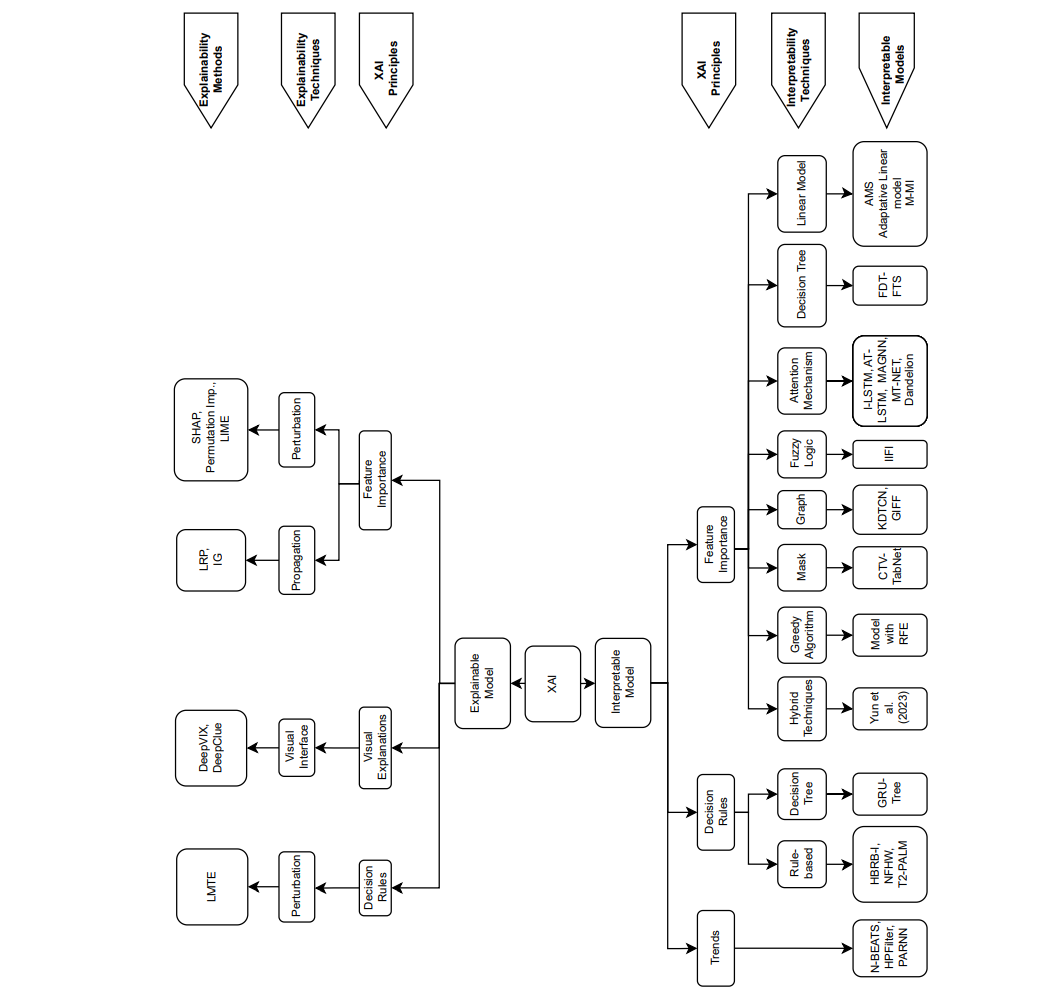
如图1所示，本文所呈现的分类法旨在帮助读者为其特定环境识别合适的XAI方法。最初，XAI方法分为可解释模型和解释方法。每个类别根据XAI的原则进一步分类，包括特征重要性、视觉解释和时间序列分析。之后，解释方法和可解释模型根据用于阐述XAI原则的技术进行分类。对于可解释模型，包括线性回归、注意力机制、决策树、图等。对于解释方法，包括扰动、传播和视觉界面。按照图1所示的图表，本文在第5和第6部分中介绍了所审查的方法。

可解释模型

本节介绍了综述中审查的可解释模型。这些模型提供了特征重要性（参见第5.1小节）、决策规则（参见第5.2小节）或关系分析，如时间序列中的趋势（参见第5.3小节）。模型可解释性的评估将在第5.4小节中讨论。

一些呈现的模型可能看起来更像黑箱模型而不是可解释模型。由于它们的复杂性，这些模型不符合传统意义上的仅包含基本模型的可解释模型定义。例如，神经网络、注意力模型和其他复杂模型通常被社区视为黑箱模型。这是因为与线性模型和决策树等基本可解释模型相比，它们更加复杂。基于这一标准，复杂模型如注意力模型将被排除在可解释模型类别之外。然而，XAI模型不是根据其复杂性分类的。为了被视为可解释模型，模型需要提供一些帮助用户理解它们的信息，特别是通过XAI原则。因此，XAI原则的来源是决定模型在可解释性和可解释性方面性质的关键因素。如果原则直接来自模型本身，则该模型被视为可解释模型。否则，如果XAI原则来自另一个算法，即解释方法，则该模型将被视为可解释模型。因此，即使一些模型是复杂的，它们仍然可以生成可以被用户解释的信息，以更好地理解模型背后的过程。这就是为什么包括我们在内的许多作者称它们为可解释模型。例如，注意力模型，如第5.1.3小节中介绍的那些，包含表示特征重要性的注意力权重。由于这些权重来自模型本身，它们被归类为可解释模型。同样，复杂神经网络也因其结构中的某个组件，如掩码[84]或模糊逻辑组件[94]，能够向用户揭示一些关于网络的信息，因此被归类为可解释模型。 可能存在其他对可解释性和可解释性的定义，这些定义可能会导致对这些复杂模型的不同分类。我们认为，本文中的定义有助于在可解释性和可解释性之间划清明确的界限，并且根据这些定义对模型进行分类是合乎逻辑且易于理解的。