如何做生成更好的视频图像？Meta&MIT最新《流匹配（Flow Matching, FM）》指南和代码

Yaron Lipman¹, Marton Havasi¹, Peter Holderrieth², Neta Shaul³, Matt Le¹, Brian Karrer¹, Ricky T. Q. Chen¹, David Lopez-Paz¹, Heli Ben-Hamu³, Itai Gat¹

¹Meta FAIR, ²麻省理工学院计算机科学与人工智能实验室（MIT CSAIL）, ³魏兹曼科学研究所 流匹配（Flow Matching, FM）是一种新兴的生成建模框架，在图像、视频、音频、语音以及生物结构等多个领域中实现了最先进的性能。本指南提供了一份全面且自成体系的FM综述，涵盖其数学基础、设计选择及其扩展内容。同时，我们还提供了一个基于PyTorch的代码包，其中包含相关示例（例如图像和文本生成），旨在为有兴趣理解、应用和进一步开发FM的初学者和资深研究人员提供资源。发布日期：2024年12月10日 代码库：https://github.com/facebookresearch/flow_matching

流匹配（Flow Matching, FM）简介

参考文献

Lipman等人, 2022; Albergo和Vanden-Eijnden, 2022; Liu等人, 2022 流匹配（Flow Matching, FM）是一个简单的生成建模框架，在包括图像生成（Esser等人, 2024）、视频生成（Polyak等人, 2024）、语音生成（Le等人, 2024）、音频生成（Vyas等人, 2023）、蛋白质建模（Huguet等人, 2024）和机器人学（Black等人, 2024）等多种领域的大规模应用中实现了最先进的成果。 本手稿及其配套代码库的主要目标包括以下两个方面：

为流匹配提供一个全面且自成体系的参考资料，详细说明其设计选择及研究社区开发的多种扩展。 1. 帮助新手快速采用并基于流匹配开发他们自己的应用。

**

**流匹配框架概述

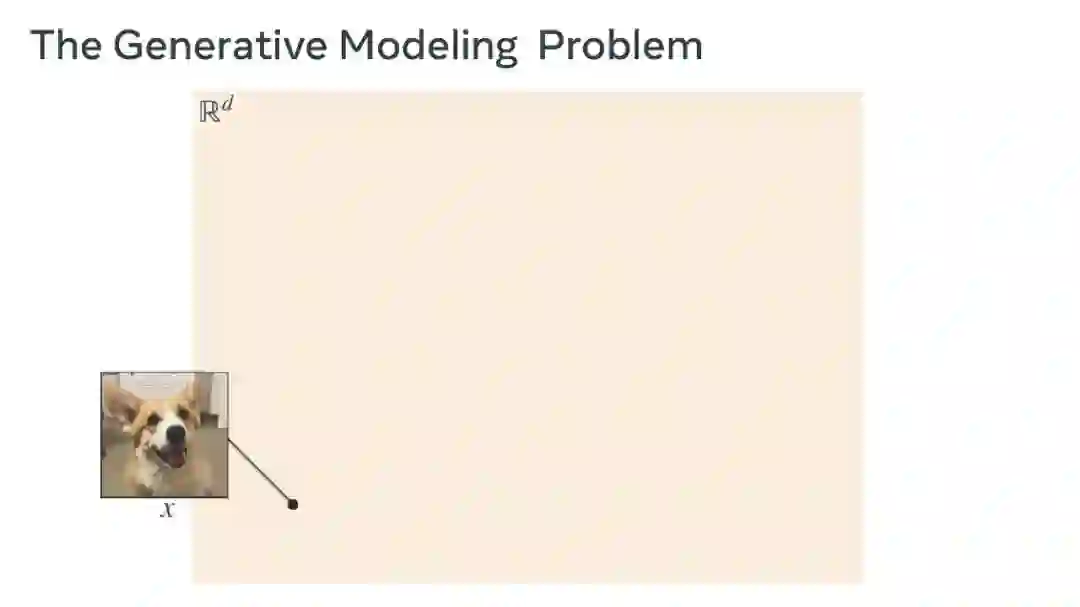
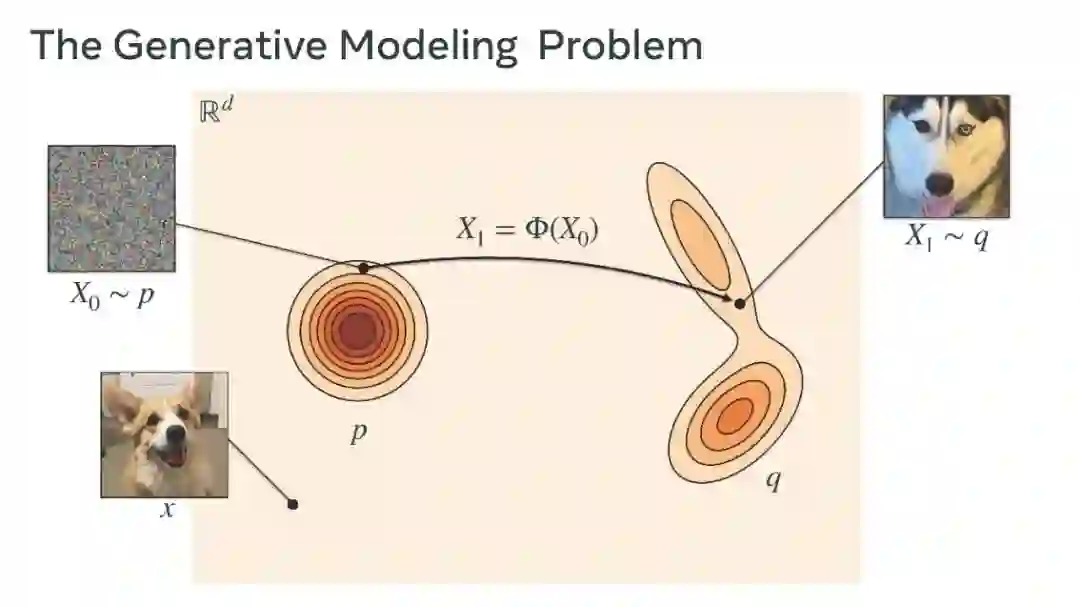
流匹配的核心是学习一个速度场（也称为矢量场）。每个速度场通过解决一个常微分方程（ODE）定义一个流ψt\psi_tψt，这一过程称为模拟。流是对d维欧几里得空间Rd\mathbb{R}^dRd的确定性、时间连续、可逆的变换。流匹配的目标是构建一个流，使其将从源分布ppp中采样的样本X0∼pX_0 \sim pX0∼p转化为目标样本X1:=ψ1(X0)X_1 := \psi_1(X_0)X1:=ψ1(X0)，从而使得X1∼qX_1 \sim qX1∼q符合目标分布qqq（见图1a）。

**流模型的历史背景

流模型最早由Chen等人（2018）和Grathwohl等人（2018）引入机器学习社区，称为连续正则化流（Continuous Normalizing Flows, CNFs）。最初，这些流通过最大化训练样本X1X_1X1的似然概率p(X1)p(X_1)p(X1)进行训练，这需要在训练期间进行模拟和对其求导。由于计算负担较重，后续研究尝试在没有模拟的情况下学习CNFs（Rozen等人, 2021; Ben-Hamu等人, 2022），最终发展为现代的流匹配算法（Lipman等人, 2022; Liu等人, 2022; Albergo和Vanden-Eijnden, 2022; Neklyudov等人, 2023; Heitz等人, 2023; Tong等人, 2023）。

**流匹配的步骤

该框架包含两个关键步骤（Lipman等人, 2022，见图2）： 1. 选择一个概率路径ptp_tpt，在源分布ppp和目标分布qqq之间插值。 1. 训练一个速度场（神经网络）定义的流变换ψt\psi_tψt，实现概率路径ptp_tpt。

**扩展到离散状态和其他过程

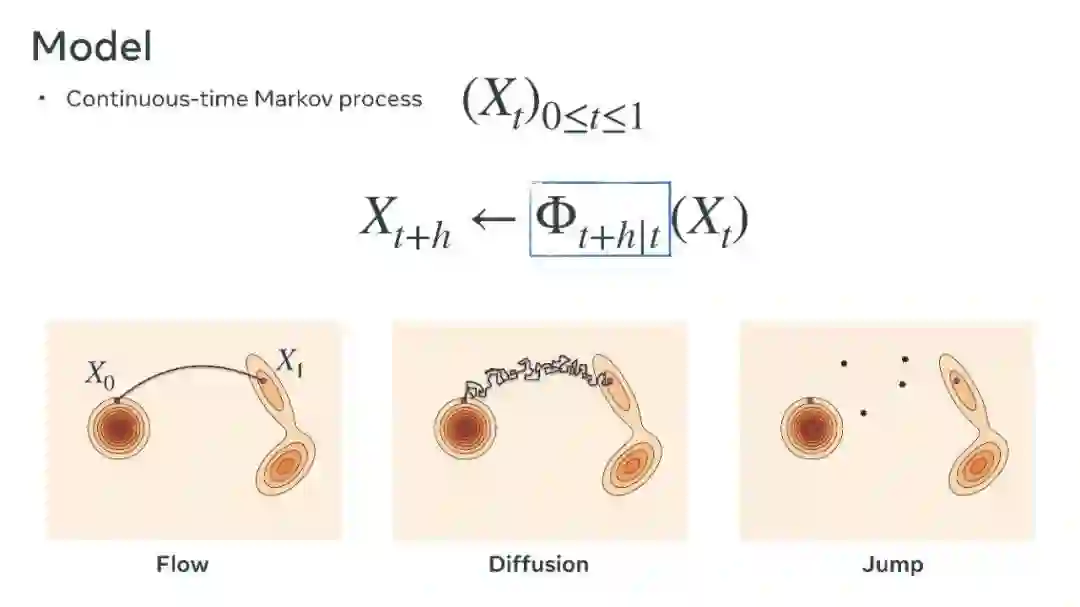
流匹配的原则可以扩展到Rd\mathbb{R}^dRd以外的状态空间SSS，甚至非流的演化过程。离散流匹配（Discrete Flow Matching, Campbell等人, 2024; Gat等人, 2024）开发了一种针对离散状态空间上的时间连续马尔可夫过程（CTMC）的流匹配算法（见图1c），为离散生成任务（如语言建模）提供了可能性。黎曼流匹配（Riemannian Flow Matching, Chen和Lipman, 2024）将流匹配扩展到黎曼流形上的流（S=MS = MS=M），目前已成为化学中许多应用（如蛋白质折叠）的最先进模型（Yim等人, 2023; Bose等人, 2023）。更一般地，生成器匹配（Generator Matching, Holderrieth等人, 2024）表明流匹配框架适用于任何模态和一般的连续时间马尔可夫过程（CTMP），包括连续空间中的流、扩散和跳跃过程，以及离散空间中的CTMC。

**生成模型的统一视角

在流匹配的视角下，扩散模型通过前向噪声过程（由特定SDE建模）构建插值路径ptp_tpt，并使用得分函数（Song和Ermon, 2019）参数化扩散过程的生成器（即漂移和扩散系数）。扩散桥（Diffusion Bridges, Peluchetti, 2023）提供了设计扩散过程生成器的新方法，使用Doob的h变换构造生成器。

**本文内容组织

本文其余部分组织如下： * 第2节提供一个“速查表”，帮助读者在PyTorch中理解和实现基础流匹配。 * 第3节讨论流模型在连续状态空间中的应用。 * 第4节介绍流匹配框架在Rd\mathbb{R}^dRd中的设计选择和扩展。 * 第5节探讨流匹配如何扩展到黎曼几何中。 * 第6节介绍连续时间马尔可夫链（CTMC）及其在离散状态空间生成模型中的应用。 * 第7节讨论流匹配在CTMC过程中的扩展。 * 第8节介绍CTMP在任意状态空间中的生成应用。 * 第9节介绍生成器匹配（GM），它统一了之前章节的所有模型，并提出了CTMP的可扩展训练方法。 * 第10节探讨去噪扩散模型作为流匹配家族模型的一个具体实例。