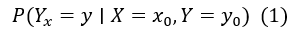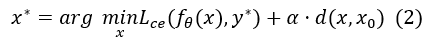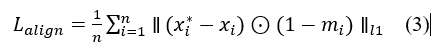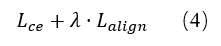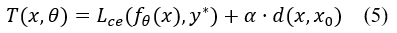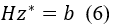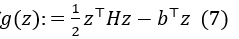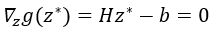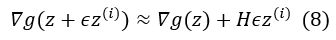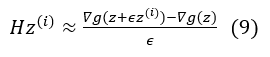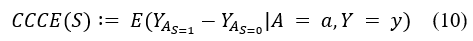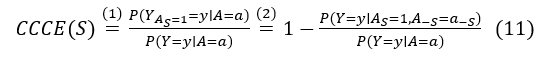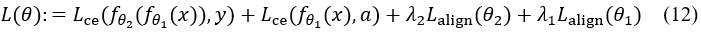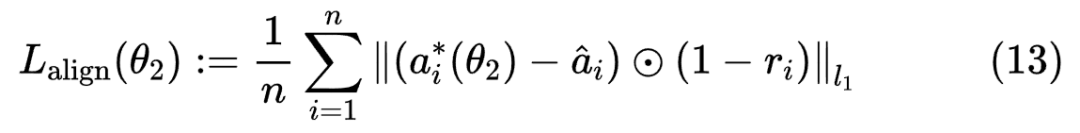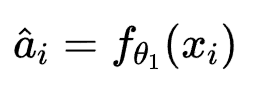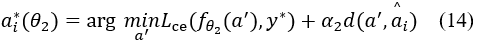ICLR 2025 | 因果对齐学习在疾病可靠诊断中的应用

关键词**：**对齐学习；反事实推断；决策模型

导 读

本文是对发表在 ICLR 2025 的论文 Learning Causal Alignment for Reliable Disease Diagnosis 的解读。该论文由北京大学王亦洲课题组、复旦大学孙鑫伟副教授和上海交通大学乔宇教授团队共同完成，第一作者为北京大学博士生刘鸣洲。

本文提出了一种旨在对齐因果决策机制的学习框架，通过反事实推断和对齐损失函数，在模型训练中引导其关注因果特征，实现模型与人的决策机制的对齐。

论文链接：

https://arxiv.org/abs/2310.01766 开源代码：

https://github.com/lmz123321/Causal_alignment

01

方法概览

在决策问题中，模型是否对齐专家的决策过程，直接决定了其决策结果的可靠性。许多已有研究尝试实现这种对齐，如通过输入梯度限制模型关注医生标注区域，或通过多任务学习同时预测标签和解释。然而，这些方法仅实现了相关性层面的对齐，模型可能仍然依赖与病灶具有伪相关性的特征，从而无法泛化。

为解决这一问题，本文提出一种因果对齐框架，旨在对齐模型和专家的因果决策机制。其核心思想是，首先通过反事实生成来识别模型自身的因果决策路径。进而，通过构造损失函数将模型的决策机制与专家的决策机制进行对齐。本文还引入了层级因果结构建模，将模型的决策机制拆解为“图像 → 属性 → 决策”的因果链进行对齐学习。在优化方面，针对反事实生成涉及的隐函数问题，本文引入隐函数定理与共轭梯度法进行高效的梯度估计。

与传统基于相关性的对齐方法相比，本文方法具有更强的可泛化性，能够显著减少对伪相关特征的依赖，提升了模型决策问题中的鲁棒性。

02

背景介绍

**问题设定。**以医学影像中的分类任务为例，我们的目标是训练一个诊断模型，使其不仅能准确预测疾病标签 y，还能在决策过程中与医生因果决策路径保持一致。具体地，对于每个样本，系统输入影像 x，输出医生标注的诊断标签 y 以及相应解释 e。其中解释由两个部分组成：病灶区域的二值掩码 m 与一组属性标签 a。我们希望学习一个从 x 预测 y 的分类器 fθ，它的预测准确且决策依据和医生认知的对齐的。

**结构性反事实建模。**为判断模型是否依赖于真正的因果特征，我们引入反事实分析框架。参考 Pearl[1]提出的定义，因果影响的概率可表示为：

即“在观测到 X=x0, Y=y0 的前提下，若将 X 干预为 x，Y 会取值为 y 的概率”。在本研究中，我们不关心整张图像，而是关注图像中哪些区域真正对模型的预测起到决定性作用。

**反事实生成。*给定原始样本 (x0, y0)，我们生成一个反事实图像x，使得模型的预测类别发生改变（即预测为y*≠y0），且图像修改尽可能小。该过程可形式化为如下优化：

其中 Lce 为交叉熵损失，d 为衡量图像改动范围的距离函数，α 为正则系数。最终，supp(x*-x0) 即为模型为预测 y0 所依赖的关键区域。

**挑战与对策。*由于反事实图像 x 是模型参数 θ 的隐函数，求解包含反事实的损失函数梯度（如因果对齐损失）并不容易。为此，本文借助隐函数定理并结合共轭梯度法进行高效的梯度估计。相关细节将在方法部分展开。

03

方 法

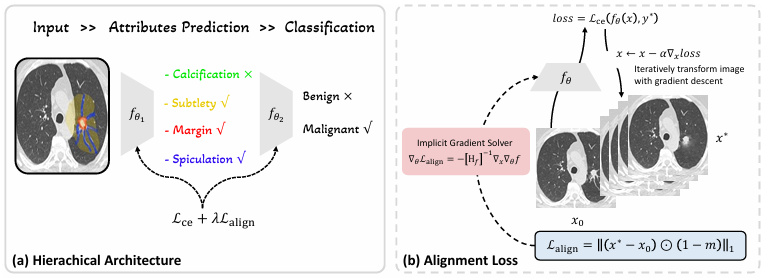
本文提出了一种因果对齐框架，以实现深度学习模型与医生决策过程在因果路径上的一致性。整体方法分为三个关键模块：因果对齐损失的设计、反事实损失的优化求解、以及层级式因果对齐策略。图1展示了整体流程。

图1. (a) 采用分层结构，先预测图像属性,再输出诊断结果。(b) 训练阶段，前向传播中生成反事实图像 x*，并根据专家标注 m 计算对齐损失 Lalign；反向传播中通过隐式梯度求解器计算梯度并更新参数 θ。

1. 因果对齐损失

传统视觉对齐方法大多依赖于输入梯度或注意力图（如CAM）对专家注释区域进行约束，然而这类方法往往容易受到伪相关特征的干扰。为此，本文基于反事实区域构造对齐损失，从源头上约束模型依赖的因果特征与医生注释区域一致。

具体而言，对于每个样本，我们生成反事实图像 x*，并以医生提供的掩码 m 为参考，定义因果对齐损失如下：

其中 xi*- xi 表示反事实修改区域。损失项鼓励模型将决策所依赖的区域限制在医生注释内，从而对齐模型与医生的因果关注点。

最终训练目标为分类损失与因果对齐损失的加权和：

2. 优化方法

如前所述，本文的因果对齐损失依赖于反事实图像 x*，而 x* 又是通过优化问题生成的，因此它是模型参数 θ 的隐函数。这导致我们无法直接使用链式法则计算损失函数对模型参数的梯度，即 Lalign 对 θ 的梯度不可显式求导。为此，本文引入了隐函数定理来间接求解梯度。

隐函数建模

假设我们将生成反事实图像的优化目标记为：

在最优解处（即 x*），该函数关于 x 的梯度为0，即：T(x*,θ) 对 x 梯度为0。

基于隐函数定理[2]，我们可以对该等式对参数 θ 求导，并得到如下梯度求解公式：

其中，z*:=∇θx*, H:=∇x2T(x*,θ) 是二阶导数（Hessian 矩阵）；b:=－∇θ(∇xT)。

然而，对于图像处理任务，通常 θ 是高维神经网络的参数，这使得计算 Hessian 矩阵及其逆变得不可行。为了解决这个问题，我们采用了共轭梯度算法[3]来估算方程的解，而不显式计算或存储 Hessian 矩阵。

根据共轭梯度的概念，解方程 (6) 等价于求解：

其中

因为最小点 z*满足：

在这种情况下，我们可以实现梯度下降法来最小化 g，其中最小点给出了方程 (6) 的解。在最小化过程中，梯度更新的方向设置为与残差 b-Hz(i) 共轭（即正交），其中 z(i) 是第 i 次迭代中 z*的估计，以实现最佳收敛速度。为了在不显式计算 H 的情况下实现这一点，我们可以利用 Hessian 向量积[4]。具体地，对于 z 附近一个小的变化，我们有：

由此得到：

3. 层次对齐

在许多医学影像任务中，医生不仅会给出疾病的最终诊断标签（如“良性”或“恶性”），还会提供一组与病灶相关的属性标签（如“边缘毛刺”“钙化”“密度”等），这些属性反映了医生在决策过程中的中间推理步骤。为了更好地模拟医生的诊断路径，本文提出了一种层级因果对齐机制，明确建模“图像 X → 属性 A → 标签 Y”的因果链条，从而提升模型的因果可解释性与可靠性。

因果图与假设

我们假设从图像 X 到属性 A 之间存在因果边。由于这些属性是直接从图像中标注的，我们假设它们之间没有额外的依赖关系，即在给定X的条件下，它们是条件独立的。在这些属性的基础上，我们进一步假设 A->Y 之间存在因果关系，表示从属性到最终决策标签的决策过程。

具体来说，我们的分类器 fθ 由两个部分组成，fθ1:X->A，它从图像 x 中预测属性，以及 fθ2:A->Y，它基于预测的属性对标签进行分类。为了生成反事实，我们首先通过改变预测的属性为反事实属性 a*，找到负责预测 y 的属性。然后，我们通过对图像的反事实优化过程，定位图像特征，这些特征解释了 |a*-a^| 的变化，并得到反事实图像 x*。对于层次对齐，我们要求 |a*-a^| 和 |x*-x^| 分别与专家对因果属性和图像区域的注释对齐。

属性注释的因果归因

尽管在许多情况下可以获得属性注释，但很难知道这些属性中哪些属性决定了放射科医生对每个特定患者的标注。为了识别用于对齐的因果属性，我们采用基于反事实因果效应的因果归因方法[5]，来量化在条件化整个属性向量的情况下，任何属性子集的因果概率。具体来说，给定属性 A=a 和标签 Y=y 的情况下，我们可以计算每个属性子集 S 的条件反事实因果效应（CCCE）得分：

CCCE(S) 是可识别的[5]，且等于：

其中 A-s 表示超出子集S的属性,公式里的 (1) 源于外生性条件，即 A 和 Y 之间没有混杂因素，公式里的 (2) 基于单调性条件，如果 a≤a’，那么 Ya≤Ya’。这两个条件在我们的场景中是自然成立的。具体来说，外生性条件成立的原因是：首先，放射科医生的决策 Y 仅基于属性；其次，对于单调性条件，对任何属性从0到1的干预（例如，从没有推测到有推测）都会提高恶性肿瘤的概率。

在计算每个属性子集的 CCCE 得分后，我们选择得分最高的子集 S 作为与标签因果相关的属性集。

层级对齐

为模拟专家“先识别属性、再作判断”的决策逻辑，我们构建了一个两阶段模型结构，并引入层次对齐机制，确保各阶段输出与因果路径一致。模型由两部分组成：fθ1(x)，从输入 x 预测结节属性 a；fθ2(a)，基于属性 a 预测最终标签 y；整体优化目标函数为：

其中，前两项为分类与属性预测的交叉熵损失，后两项为对齐损失。

属性-标签对齐通过以下损失函数实现：

其中：

为当前属性预测。

ai*(θ2) 是在标签 y 发生变化条件下，以下目标函数最小化后生成的反事实属性：

输入－属性对齐通过如下构造：

即在属性变更的条件下，寻找最小扰动的输入 xi*，使模型预测出新的属性。

基于目标函数（公式12），我们对参数 θ 进行优化时，将算法1应用于各对齐项。优化完成后，模型的决策流程 y:=fθ2(fθ1(x)) 与专家的推理路径高度一致：其中 fθ1 利用图像中的因果因素预测中间属性，fθ2 则基于这些因果属性进一步预测最终标签 y。

04

实 验

我们在 LIDC-IDRI 数据集（用于肺结节分类）和 CBIS-DDSM 数据集（用于乳腺肿块分类）上进行实验。为评估模型学习与专家一致特征的能力，我们在每张图像左上角添加一个正负符号，作为伪相关特征。在训练集中，符号与恶性标签相关联（y = 1 时标注“+”，y = 0 时标注“-”），但在验证集和测试集中则随机分配。一个合理对齐的模型应关注医生标注区域而非该符号。

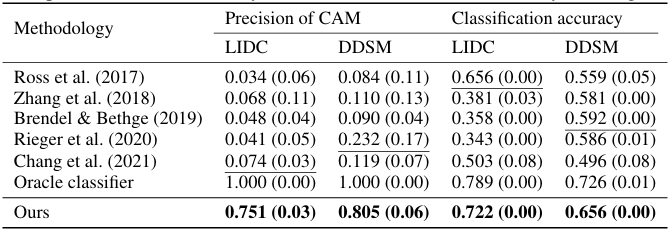
本文将所提方法与一系列具代表性的可解释性基线方法进行了对比。由图2可见，我们的方法在两个指标上均显著优于除 Oracle 外的所有基线，充分体现了其在因果特征建模方面的优势。相比于仅捕捉表面相关性的伪特征，本方法关注的区域具备真实的因果关系，因而在测试集上具有更强的泛化能力。

图2. 在 LIDC-IDRI 和 CBIS-DDSM 数据集上与基线方法的比较。表中加粗表示我们方法的结果，下划线表示各基线方法中的最优结果。

05

结 论

本文提出了一种因果对齐框架，用以缩小机器学习模型与专家在决策过程中的差距。通过识别影响模型决策的因果特征，并引入因果对齐损失函数，我们实现了模型激活区域与专家关注区域的一致性，从而训练出贴近专家诊断流程的分层决策模型。实验结果在肺癌和乳腺癌诊断任务中均验证了该方法的有效性。

参考文献：

[1] Judea Pearl. Causal inference in statistics: An overview. 2009. [2] Steven George Krantz and Harold R Parks. The implicit function theorem: history, theory, and applications. Springer Science & Business Media, 2002. [3] Nisheeth K Vishnoi et al. Lx= b. Foundations and Trends® in Theoretical Computer Science, 8 (1–2):1–141, 2013. [4] Lili Song and Luis Nunes Vicente. Modeling hessian-vector products in nonlinear optimization: new hessian-free methods. IMA Journal of Numerical Analysis, 42(2):1766–1788, 2022. [5] Ruiqi Zhao, Lei Zhang, Shengyu Zhu, Zitong Lu, Zhenhua Dong, Chaoliang Zhang, Jun Xu, Zhi Geng, and Yangbo He. Conditional counterfactual causal effect for individual attribution. In Uncertainty in Artificial Intelligence, pp. 2519–2528. PMLR, 2023.