基于强化学习的扩散模型微调：教程与综述

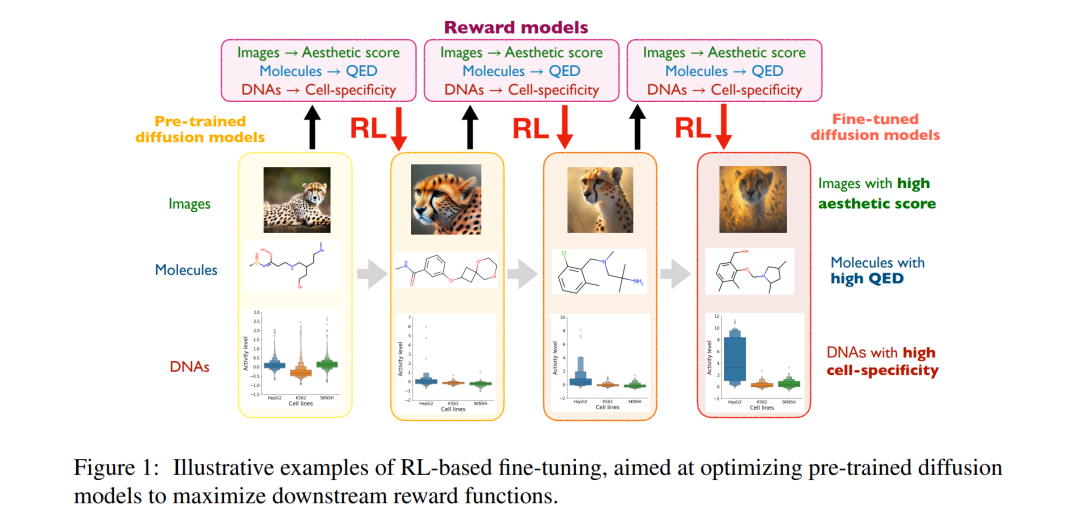
本教程全面调查了用于微调扩散模型以优化下游奖励函数的方法。虽然扩散模型因其出色的生成建模能力广为人知，但在生物学等领域的实际应用中，需要生成最大化某些期望指标（如RNA的翻译效率、分子的对接评分、蛋白质的稳定性）的样本。在这些情况下，扩散模型不仅可以生成逼真的样本，还可以明确地最大化感兴趣的度量。这些方法基于强化学习（RL）的概念。我们解释了各种RL算法的应用，包括PPO、可微优化、奖励加权最大似然估计（MLE）、价值加权采样和路径一致性学习，这些算法专门用于微调扩散模型。我们旨在探索基本方面，例如不同RL微调算法在各种场景中的优缺点、RL微调相对于非RL方法的好处，以及RL微调的正式目标（目标分布）。此外，我们还将探讨它们与相关主题的联系，如分类器指导、Gflownets、基于流的扩散模型、路径积分控制理论和从非标准化分布（如MCMC）中采样。本教程的代码可在https://github.com/masa-ue/RLfinetuning Diffusion Bioseq获得。

扩散模型（Sohl-Dickstein等，2015；Ho等，2020；Song等，2020）被广泛认为是强大的生成建模工具。它们能够通过紧密模拟训练数据的特征来准确地建模复杂的分布。扩散模型在多个领域有许多应用，包括计算机视觉（Podell等，2023）、自然语言处理（Austin等，2021）、生物学（Avdeyev等，2023；Stark等，2024；Li等，2023）、化学（Jo等，2022；Xu等，2022；Hoogeboom等，2022）以及生物学（Avdeyev等，2023；Stark等，2024；Campbell等，2024）。尽管扩散模型在捕捉训练数据分布方面表现出显著的能力，但常常需要根据特定的下游奖励函数对这些模型进行定制。例如，在计算机视觉领域，Stable Diffusion（Rombach等，2022）作为一个强大的预训练模型骨干，但我们可能希望通过优化下游奖励函数（如美学评分或人类对齐评分（Black等，2023；Fan等，2023））来进一步微调它。同样，在生物学和化学等领域，已经开发出各种复杂的扩散模型用于DNA、RNA、蛋白质序列和分子，有效地建模生物和化学空间。然而，生物学家和化学家通常旨在优化特定的下游目标，如DNA序列中的细胞特异性表达（Gosai等，2023；Lal等，2024；Sarkar等，2024）、RNA序列的翻译效率/稳定性（Castillo-Hair和Seelig，2021；Agarwal和Kelley，2022）、蛋白质序列的稳定性/生物活性（Frey等，2023；Widatalla等，2024）或分子的QED/SA评分（Zhou等，2019）。为了实现这一目标，已经提出了许多通过强化学习（RL）微调扩散模型的算法（如Black等，2023；Fan等，2023；Clark等，2023；Prabhudesai等，2023；Uehara等，2024），旨在优化下游奖励函数。RL是一种机器学习范式，代理通过学习进行顺序决策以最大化奖励信号（Sutton和Barto，2018；Agarwal等，2019）。在我们的背景下，RL由于扩散模型固有的顺序结构，自然而然地成为一种合适的方法，其中每个时间步涉及一个“决策”，对应于该步样本的去噪方式。本教程旨在回顾最近的研究成果，为对从整体角度理解基于RL的微调基础知识感兴趣的读者提供帮助，包括基于RL的微调相对于非RL方法的优势、不同RL微调算法的优缺点、RL微调的正式目标及其与分类器指导等相关主题的联系。本教程的内容主要分为三个部分。此外，作为实现示例，我们还发布了利用RL微调进行引导的生物序列（DNA/RNA）生成的代码，地址为：https://github.com/masa-ue/RLfinetuning Diffusion Bioseq。

我们旨在提供当前算法的全面概述。特别是，鉴于扩散模型的顺序特性，我们可以自然地将微调框架为马尔可夫决策过程（MDP）中的强化学习（RL）问题，如第3和第4节所述。因此，我们可以采用任何现成的RL算法，例如PPO（Schulman等，2017）、可微优化（直接奖励反向传播）、加权MLE（Peters等，2010；Peng等，2019）、价值加权采样（类似于Dhariwal和Nichol（2021）中的分类器指导）以及路径一致性学习（Nachum等，2017）。我们在第4.2和第6节详细讨论了这些算法。我们不仅仅列出每个算法，还旨在呈现它们的优缺点，以便读者可以根据自己的具体目的选择最合适的算法。
我们在第7节根据奖励反馈的获取方式分类了各种微调场景。这一区分对实际算法设计至关重要。例如，如果我们可以获得准确的奖励函数，计算效率将成为我们的主要关注点。然而，在奖励函数未知的情况下，必须从具有奖励反馈的数据中学习它们，从而需要考虑反馈效率和分布转移的问题。特别是，当需要从静态离线数据中学习奖励函数而没有任何在线交互时，我们必须解决过度优化的问题，即微调模型被分布外样本误导，生成低真实奖励的样本。这一点非常重要，因为在离线场景中，具有反馈的离线数据分布的覆盖范围有限，因此分布外区域可能非常广泛（Uehara等，2024）。
我们详细讨论了基于RL的微调方法与文献中密切相关的方法之间的关系，如第8节中的分类器指导（Dhariwal和Nichol，2021）、第9节中的基于流的扩散模型（Liu等，2022；Lipman等，2023；Tong等，2023）、第10节中的非标准化分布采样（Zhang和Chen，2021）、第6.3节中的Gflownets（Bengio等，2023）以及第6.2.3节中的路径积分控制理论（Theodorou等，2010；Williams等，2017；Kazim等，2024）。我们总结了以下关键信息：

第6.3节：Gflownets中使用的损失本质上等同于从一种特定RL算法——路径一致性学习中导出的损失。
第8节：在条件生成中使用的分类器指导被视为一种特定的基于RL的微调方法，我们称之为价值加权采样。正如Zhao等（2024）中形式化的那样，这一观察表明，任何现成的基于RL的微调算法（如PPO和可微优化）都可以应用于条件生成。
第10节：从非标准化分布（通常称为吉布斯分布）中采样在各个领域都是一个重要且具有挑战性的问题。尽管MCMC方法传统上用于解决这一任务，但认识到其与基于RL的微调目标的相似性，表明现成的RL算法也可以有效地解决从非标准化分布中采样的挑战。