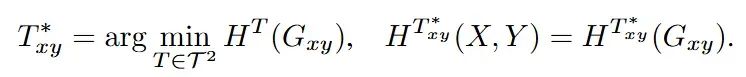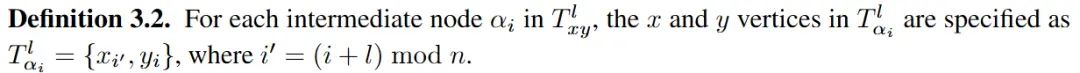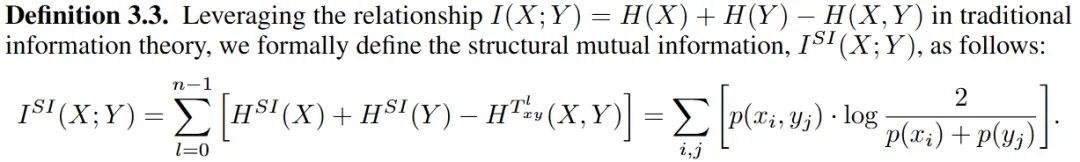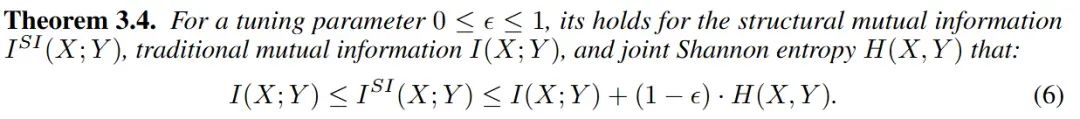【NeurlPS2024】结构信息原理指导的高效智能体探索

本文介绍来自北京航空航天大学彭浩老师团队发表在NeurlPS 2024上的一篇文章“Effective Exploration Based on the Structural Information Principles”。为了解决当前基于传统信息论的探索方法由于忽略状态-动作空间内在结构而导致效率低下的问题，作者提出了一种基于结构信息原理的探索框架，即SI2E。SI2E通过定义结构互信息，提出一种新的状态动作表征原则，捕捉状态-动作对之间的动态关系，构建最优编码树。通过分析状态-动作对之间的价值差异，定义策略条件结构熵，构造内在奖励机制，实现对于状态-动作空间更为有效的覆盖。在MiniGrid、MetaWorld和DeepMind Control Suite等测试环境中，SI2E在最终性能与采样效率等方面的表现遥遥领先，最大提升幅度分别达到了37.63%和60.25%。 论文名称：Effective Exploration Based on the Structural Information Principles 论文链接：Effective Exploration Based on the Structural Information Principles 代码链接：https://github.com/SELGroup/SI2E

1. 引言

在强化学习（RL）领域，智能体探索和利用行为之间平衡至关重要，尤其在高维度观测和稀疏奖励的场景中。最近，基于传统信息论的探索方法在自监督设置中最大化对于状态空间与动作空间的覆盖，以优化智能体策略并减轻次优结果的风险。然而，上述方法存在两个挑战，目前尚未解决：

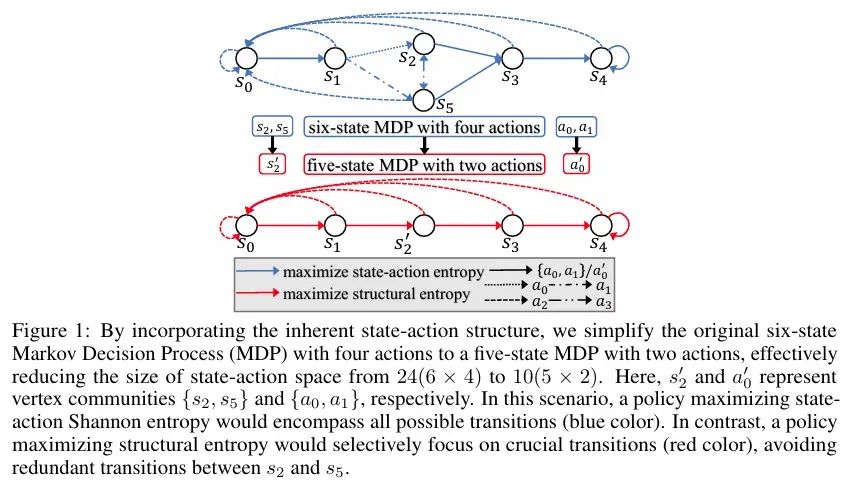
挑战1：传统最大熵策略容易受到价值分布影响，导致偏向于低值状态的不平衡探索 为减轻这一问题，该团队引入了以策略值为条件的高维结构熵。基于对状态-动作对的价值估计解析层次化社区结构，并依据智能体探索行为定义内在奖励，构建奖励塑形机制，在最大化整个状态-动作空间的覆盖的基础上，避免对于低值社区的无效覆盖。 挑战2：当前的结构信息研究存在单一变量限制，并未涉及对多变量之间的关系建模 在这项工作中，作者提出了结构互信息的概念，首次实现对于多变量之间结构相似性的度量，进一步提出对于状态-动作对的表征原则，在捕捉环境动态信息的同时，避免无效的观测干扰。 图1说明了一个简单的六状态马尔可夫决策过程 (MDP)，其中包含四个动作。如图例所示，蓝线和红线的不同密度代表不同的动作，导致状态转换，旨在返回初始状态$s_0$。实线特别表示动作$a_0$和$a_1$。状态$s_2$和$s_5$之间的转换被视为冗余，因为它们不利于实现有效返回$s_0$的主要目标。因此，状态-动作对$(s_2,a_3)$和$(s_5,a_3)$具有较低的策略值。最大化状态-动作香农熵的策略将涵盖所有可能的转换（蓝色）。相反，整合固有状态-动作空间结构的最大熵策略会将这些冗余的状态-动作对划分为顶点子社区，并最小化该子社区的熵以避免不必要地访问它。同时，它最大化了状态-动作熵，从而最大限度地覆盖了更有可能在简化的五状态 MDP 中促成期望结果的转换（红色）。 2. 结构互信息 该团队解决了现有结构信息原理中普遍存在的单变量约束，并引入了结构互信息的概念，以便在SI2E 框架内进行后续的状态-动作表示学习。 给定随机变量对(X,Y)，|X|=|Y|=n，构造一个带权无向二分图$G_{xy}$来表示X和Y变量间的联合分布，同时限制该图上的编码树为二层近似二叉结构，并得到最优的近似二叉树$T_{xy}^*$：

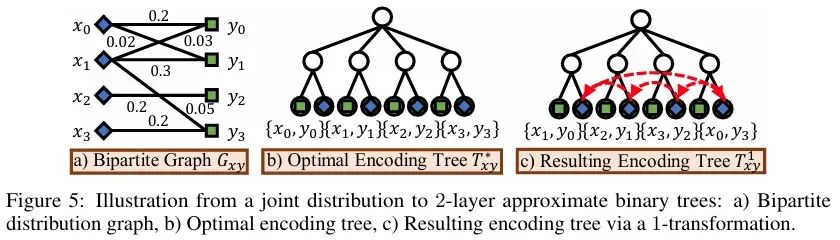
最优近似二叉树$T_{xy}^$中的每个中间节点α对应一个包含单一顶点x与单一顶点y的子集，从而在变量X与Y之间建立一个一一匹配结构。对于$T_{xy}^$中从左到右排序的第i个中间节点标记为$α_i$，在对应的子集中x和y顶点分别被标记为$x_i$和$y_i$。 为了准确定义结构互信息，需要考虑不同划分结构下两个变量的联合熵。作者引入一个应用于$T_{xy}^*$的$l-$转换算子，以系统地遍历这些变量的所有潜在一对一匹配结构，从而提供对于结构相似性的全面度量。给定一个整数参数$l>0$，该算子生成一个新的二层近似二叉树$T_{xy}^l$。

下图给出了一个对于上述过程的直观解释。

结构互信息定义：

结构互信息与传统互信息之间的关系：

3. SI2E框架设计

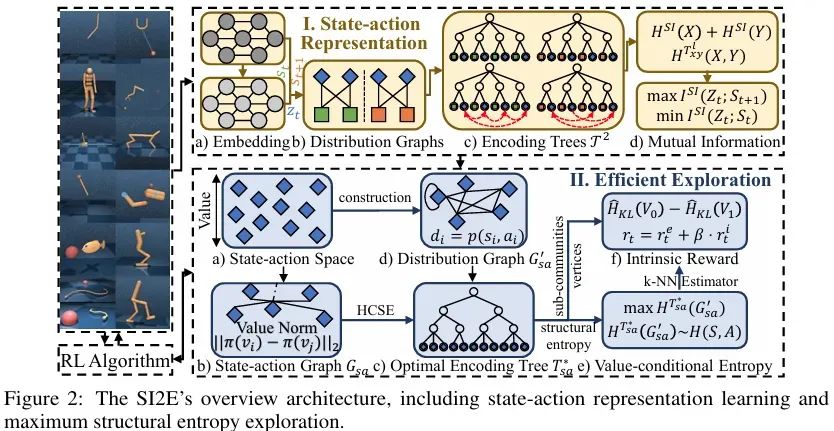
所提出SI2E框架的详细设计如下图所示，主要包含状态动作表征与智能体探索模块。

3.1 状态动作表征

3.1.1 结构互信息原理 为了有效地学习与环境动态信息相关的状态-动作表示，作者提出了一种创新的表征原则，该原则最大化了与后续状态的结构互信息，并最小化了与当前状态的结构互信息。 在该阶段，作者利用编码器$f_s$和$f_z$将当前观察值$O_t$和$O_{t+1}$表示为状态$S_t$和$S_{t+1}$，并生成对于元组$(S_t,A_t)$的潜在表示$Z_t$。通过构建无向二部图$G_{zs}$和$G_{zs'}$，作者分析$Z_t$与当前状态$S_t$和随后状态$S_{t+1}$的联合分布。通过计算互信息$I^{SI} (Z_t; S_t)$和$I^{SI} (Z_t; S_{t+1})$，作者基于信息瓶颈(IB)，提出了一种表征原则，旨在最小化$I^{SI} (Z_t; S_t)$同时最大化$I^{SI} (Z_t; S_{t+1})$。当$Z_t$与$S_{t+1}$之间的联合分布呈一一对应时，它们的互信息达到最大值，这表明每个$Z_t$值都有唯一$S_{t+1}$值与之对应，反之亦然。因此，结构互信息可以被认为是获取动态相关状态-行为表示的理想学习目标。 3.1.2 表征学习目标

在研究中，由于直接最小化$I^{SI} (Z_t; S_t)$存在计算挑战，作者提出了一个变分上界$I(Z_t; S_t) + H(Z_t |S_t) + H(S_t)$，将最小化$I^{SI} (Z_t; S_t)$转化为最小化$I(Z_t; S_t)$和$H(Z_t |S_t)$。通过利用一个可行的解码器来近似$Z_t$的边缘分布，得出了$I(Z_t; S_t)$的一个上界。同时，为了降低条件熵$H(Z_t |S_t)$，作者引入了一个预测目标，通过解码器$q_{z|s}$来近似条件概率$p(z_t |s_t)$。同时，为了有效优化$I^{SI} (Z_t; S_{t+1})$，作者最大化其下界$I(Z_t; S_{t+1})$。通过使用一个替代解码器$q_{z|s}$来近似条件概率$p(S_{t+1} |Z_t)$，得到了$I(Z_t; S_{t+1})$的一个下界。 3.2 最大结构熵探索 作者设计了一个独特的内在奖励机制，以解决传统熵策略中对低价值状态的不平衡探索的挑战。具体来说，基于策略函数生成了状态-动作空间的层次化社区结构，并依据智能体访问概率定义价值条件结构熵，实现更为有效的最大化覆盖探索。 3.2.1 分层状态-动作结构 作者从智能体与环境的交互历史中提取状态-动作对，形成一个完整的图$G_{sa}$，其中反映了智能体策略引起的价值关系。在这个图中，任意两个顶点$v_i$和$v_j$通过一条无向边连接，其权重$w_{ij}$由状态-动作对$(s_t^i,a_t^i)$和$(s_t^j,a_t^j)$的策略值差异确定。通过最小化图$G_{sa}$的二维结构熵，生成了二层最优编码树$T_{sa}^$。该树描述了状态-动作顶点之间的分层社区结构，根节点涵盖所有顶点，每个中间节点对应于一个子社区，其中的顶点共享相似的策略值。 3.2.2 值条件结构熵 为了衡量智能体探索在状态-动作空间中的覆盖程度，作者构建了一个额外的分布图$G'{sa}$，与原图$G{sa}$共享相同的顶点集。对于所有状态-动作对，给定正的访问概率，作者证明了该加权、无向、连通图$G'{sa}$的存在性，其中每个顶点的度数与其访问概率成正比。 在图$G'{sa}$中，状态-动作顶点集合为$V_0$，状态-动作子社区集合为$V_1$。与这些集合的访问概率分布相关联的香农熵分别表示为$H(V_0)$和$H(V_1)$，其中$H(V_0)$等同于整个状态-动作空间的香农熵。在二层状态-动作社区$T_{sa}^$内，定义了$G'{sa}$的结构熵$H^{T{sa}^* } (G'{sa})$。理论证明了结构熵$H^{T{sa}^* } (G'{sa})$和香农熵$H(S_t,A_t)$之间存在如下关系： $ζ · H(S_t,A_t) ≤ H(V_0) - H(V_1) ≤ H^{T{sa}^* } (G'{sa}) ≤ H(S_t,A_t)$ 其中，$H(V_0) - H(V_1)$是$H^{T{sa}^* } (G'_{sa})$的一个变分下界。因此，在确保整个状态-动作空间最大覆盖的同时，缓解了状态-动作子社区之间不均匀覆盖的问题。通过识别智能体策略引起的分层状态-动作结构，SI2E实现了更为有效的最大覆盖探索，确保了其探索优势。 3.2.3 评估和内在奖励

在面对直接获取访问概率的不可行性时，作者研究采用了k-NN熵估计器来估计条件结构熵下界，以评估状态-动作空间的覆盖程度。通过使用这个估计器得到的结果，可以定义内在奖励，并结合外部任务奖励，训练强化学习智能体来解决目标任务。

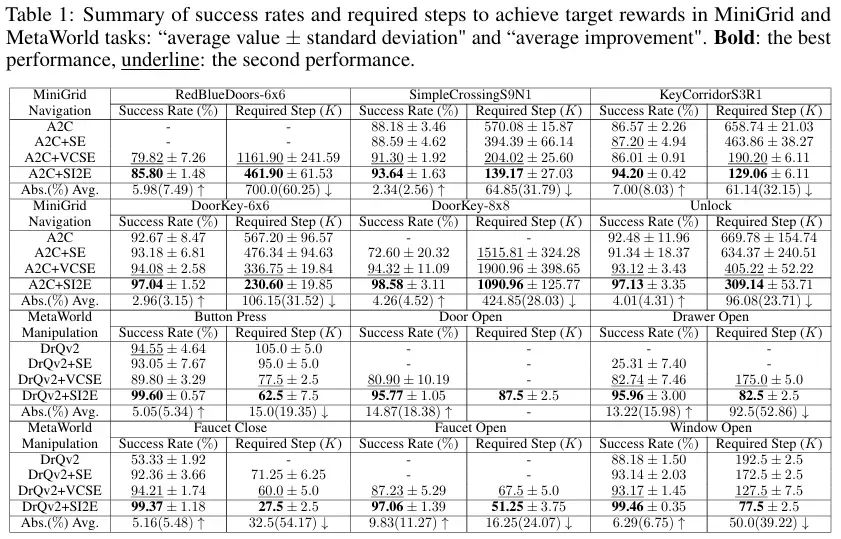
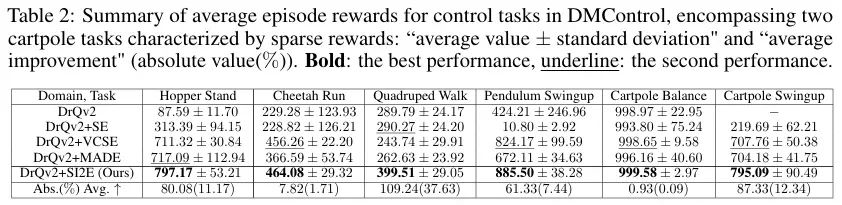
4. 实验与评估 为了验证该框架的性能优势，作者在MiniGrid、MetaWorld和DMControl等环境中进行了一系列综合性的对比实验。 4.1 MiniGrid实验对比 在MiniGrid基准测试中，作者评估了SI2E在导航任务中的表现，这些任务旨在在稀疏奖励环境中实现目标。该设置是部分可观察的，智能体接收到周围网格的7×7×3嵌入而不是整个网格环境。作者采用A2C智能体作为基准，并将香农熵和基于价值的状态熵（VCSE）作为对比。实验结果显示，在各种导航任务中，包括带障碍物的导航、长期导航以及带障碍物的长期导航，如表1所示，SI2E在最终性能和样本效率方面表现出显著改善。 4.2 MetaWorld实验对比 作者进一步在MetaWorld基准测试中的视觉操作任务上评估SI2E框架，该基准测试由于其庞大的状态空间而提出了探索性挑战。作者选择DrQv2算法作为基础RL方法。采用相同的摄像头配置，并将奖励标准化为1。同时，表1中总结了所有探索方法在六个MetaWorld任务中的成功率和所需步骤，从而证明了SI2E的性能优势。 4.3 DMControl实验对比 此外，该团队在DMControl套件中的连续控制任务中对SI2E框架进行了评估，同样选用了DrQv2算法作为基础智能体，该算法基于像素观察进行操作。为了更全面地比较，引入了MADE作为状态-动作探索基线。通过评估六个连续控制任务中所有探索方法的表现并记录在表2中，观察结果显示，SI2E显著提高了每个DMControl任务的平均集奖励。

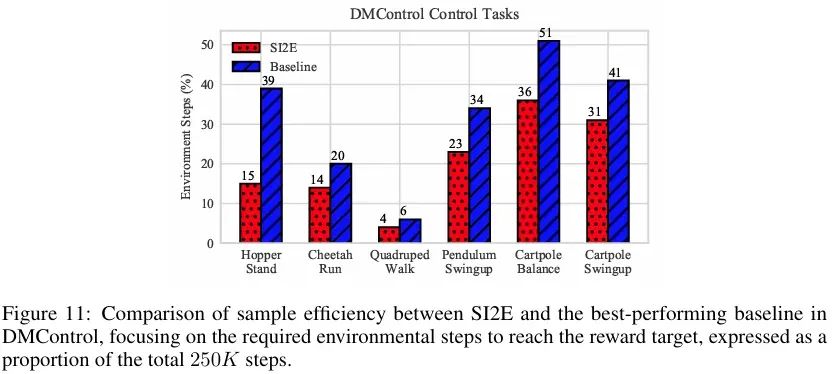
下图中对比了SI2E和最佳基线的样本效率。这些结果不仅展示了SI2E在获取与动态相关的状态-动作表示方面的有效性，还突显了其激励智能体探索状态-动作空间的潜力。

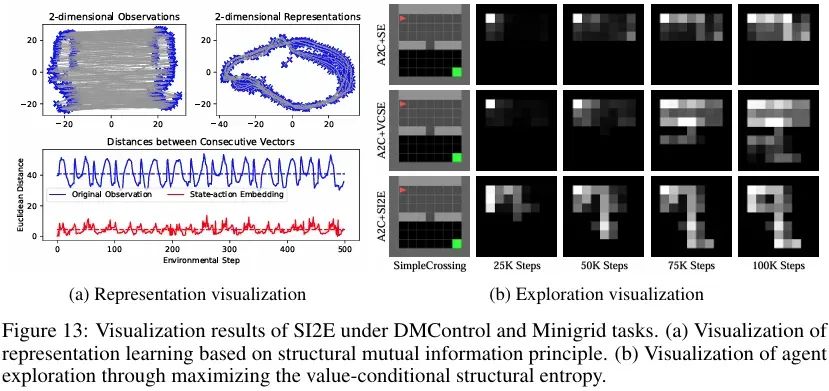
为了更好地理解SI2E框架的合理性和优势，下图提供了SI2E表征结果与探索行为的可视化实验：(a) 基于结构互信息原理的表示学习可视化，(b) 通过最大化价值条件结构熵实现智能体探索的可视化。

4.4 消融实验

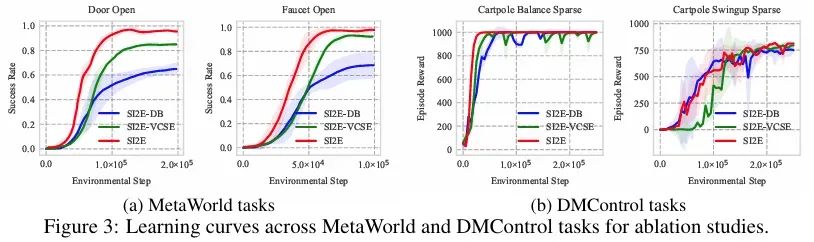
通过对MetaWorld和DMControl任务进行消融实验，作者专注于研究SI2E框架中嵌入原则和内在奖励机制这两个关键组成部分的影响。关注了两个不同变体：(i) SI2E-DB，利用DB瓶颈来学习状态-动作表示，(ii) SI2E-VCSE，采用最先进的VCSE方法来计算内在奖励。结果显示，如下图所示，SI2E在最终性能和样本效率方面均优于所有变体，这表明这些关键组件在赋予SI2E卓越能力方面起着重要作用。

5. 结论及展望

作者提出了一种基于结构信息原理的新型智能体探索框架SI2E。该框架定义了结构互信息，以有效捕获与环境动态相关的状态-动作表示。它最大化了以价值为条件的高维结构熵，以增强对于整个状态-动作空间更为有效的覆盖。同时，建立了SI2E与传统信息论探索方法之间的理论联系，凸显了该框架的合理性和优势。通过广泛的对比评估，与最先进的探索方法相比，SI2E显著提高了最终性能和取样效率。作者未来的工作包括扩展编码树的高度和实验环境的范围。作者的目标是让SI2E在强化学习中保持一个强大和适应性强的工具，特别适合高维和稀疏奖励的环境。 篇幅原因，我们在本文中省略了诸多细节，更多细节可以在论文中找到。感谢阅读！