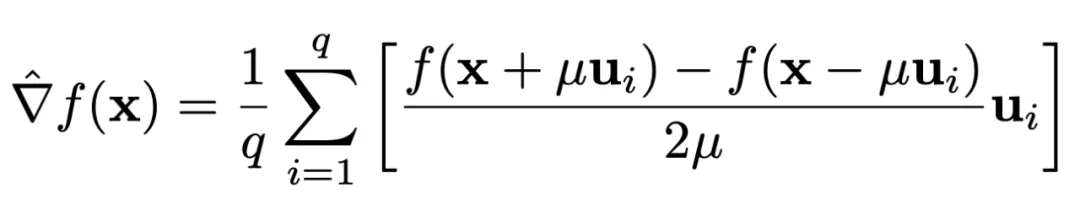【ICML 2024】零阶优化器微调大模型，大幅降低内存

转载机器之心

开源大语言模型（LLM）百花齐放，为了让它们适应各种下游任务，微调（fine-tuning）是最广泛采用的基本方法。基于自动微分技术（auto-differentiation）的一阶优化器（SGD、Adam 等）虽然在模型微调中占据主流，然而在模型越来越大的今天，却带来越来越大的显存压力。因此，如何高效地在微调中降低显存使得单卡可以满足微调需求已经成为一个热门研究问题。值得注意的是，虽然反向传播是这些一阶优化器的基石，被用于计算神经网络每个权重的梯度，同时却也是显存杀手，其中庞大计算图的保存所带来的开销也在大模型时代被凸显得尤为突出。与此同时，零阶优化器（Zeroth-Order Optimization）则完全无需保存计算图，转而使用有限差分来近似计算网络的梯度，通过完全避免反向传播（back-propagation; BP）来大大减少神经网络更新中的内存开销。

类似于一阶优化器中随机梯度下降的各式变种，零阶优化器也有着各种此前无人探索的改进算法。近日，来自密歇根州立大学、北卡罗来纳大学教堂山分校、德克萨斯大学奥斯汀分校、明尼苏达大学双城分校、IBM 研究中心、普林斯顿大学、以及阿里巴巴达摩院的众多研究者联合推出全面评测（benchmark）文章：Revisiting Zeroth-Order Optimization for Memory-Efficient LLM Fine-Tuning: A Benchmark 。这篇文章覆盖六种无需反向传播（BP-free）的优化器、五类大模型、三种复杂度的各项任务、四类微调方案，以及三项增强零阶优化器的全新算法。目前，相关论文已被 ICML 2024 高分接收，代码已开源；详情如下。

• 论文地址：https://arxiv.org/abs/2402.11592
• 代码地址：https://github.com/ZO-Bench/ZO-LLM
• 零阶优化讲义地址 (AAAI 2024 Tutorial)：https://sites.google.com/view/zo-tutorial-aaai-2024/

零阶优化器是什么？为何如此重要？

零阶优化器（Zeroth-Order Optimization）仅仅依靠神经网络的输出进行梯度估计，以完全不需要计算反向传播和极少的内训消耗而闻名。尽管在零阶优化器领域也存在不同的梯度估计方法，本文特指基于随机梯度估计器（Random Gradient Estimator, RGE）的一系列算法。简单来说，就是通过从高斯分布中抽取的随机扰动来计算有限差分，并将其作为梯度的近似估计，RGE 数学公式如下所示。

在此之前，零阶优化已经大量应用于机器学习问题中，比如对抗样本生成和防御，黑箱模型解释，强化学习和自动机器学习；详细的算法和应用介绍请参看 [1]。在大模型领域，MeZO [2] 率先提出将零阶随机梯度下降法（ZO-SGD）用作大模型微调，并展示了零阶优化器的无限潜力。于此同时，ZO-SGD 是最简单、基本的 BP-free 优化器，它的许多更高级的变种 [3] 能否在大模型微调领域带给我们更多惊喜，是一个亟待研究的课题。本文系统地评测了以下无需反向传播（BP-free）的优化算法在大模型微调任务上的性能、效率和兼容性，目的是向社区展示零阶优化器在多种大模型任务上的广泛潜力：

• ZO-SGD：零阶随机梯度下降 [4]
• ZO-SGD-Sign：基于符号的（sign-based）零阶随机梯度下降 [5]
• ZO-SGD-MMT：带有动量（momentum）的零阶随机梯度下降 [6]
• ZO-SGD-Cons：保守（conservative）梯度更新的零阶随机梯度下降 [7]
• ZO-Adam：零阶 Adam 优化器 [8]

本研究还包括了 Forward-Grad [9] 方法，该方法基于沿随机方向向量的方向导数来无偏估计梯度。值得注意的是，Forward-Grad 虽然不直接使用梯度回传，但是却仍然用到了自动微分算法，因此它是一种一阶的 BP-free 算法。 综上所述，本文的评测包含了上述 5 种零阶优化器以及 Forward-Grad 方法，同时对比一阶优化器中最常用的 FO-SGD 和 FO-Adam。在具体微调形式上，评测全面覆盖了 5 种 LLM 架构（RoBERTa, OPT, LLaMA, Vicuna, Mistral），3 种不同复杂度的任务（SST2, COPA, WinoGrande），以及 4 种微调方案（full-tuning, LoRA, prompt tuning, prefix tuning）。 大模型微调准确性评测

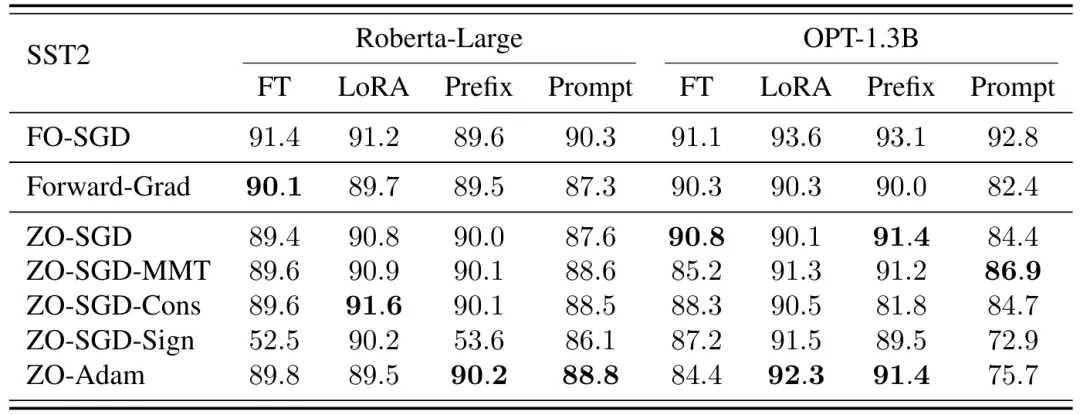
作者指出，为了有效地利用零阶优化器对大型模型在下游任务上进行微调，必须合理地运用输入模板，以便将下游任务与预训练任务进行对齐。例如对于 SST2 来说，使用模板 “ SENTENCE. It was [terrible|great]. ” 能够在 ZO-SGD 上带来约 10% 的性能提升。然而对于一阶优化器（如 FO-SGD），无论是否使用模板性能差异都不大，衬托出零阶优化器的独特性。 SST2 作为一个较为基础的任务，其实验结果可以支持以下结论：

• ZO-Adam 似乎是最有效的零阶优化器：在 8 个微调设置中的 4 个中表现最佳。
• Forward-grad 是一种竞争力强但以前被忽视的方法，特别是在全模型微调 (full fine-tuning) 中。
• ZO-SGD-Cons 和 ZO-SGD-MMT 也展示了强大的性能，而 ZO-SGD-Sign作为最简单的零阶优化器，往往是最弱的方法。

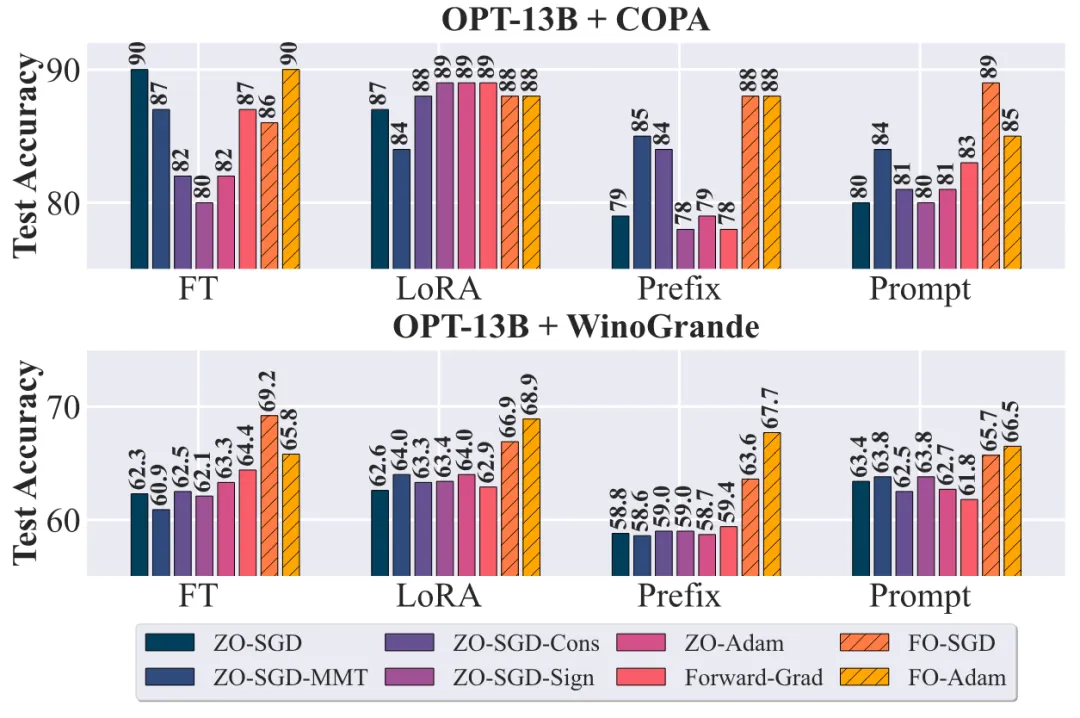
进一步，该研究使用更大的模型 OPT-13B，在更复杂、更困难的任务（COPA 和 WinoGrande）上进行实验，得出以下结论：

• 在更复杂的任务中，不同优化器的性能差异被进一步放大。
• ZO-Adam 和 ZO-SGD-MMT 在各种实验下展示了非常好的稳定性，这可能归因于减少了方差的设计。
• LoRA 微调对于零阶算法始终表现出强大的鲁棒性，在各种实验环境中稳定且可靠。

---

**大模型微调内存开销评测与详解

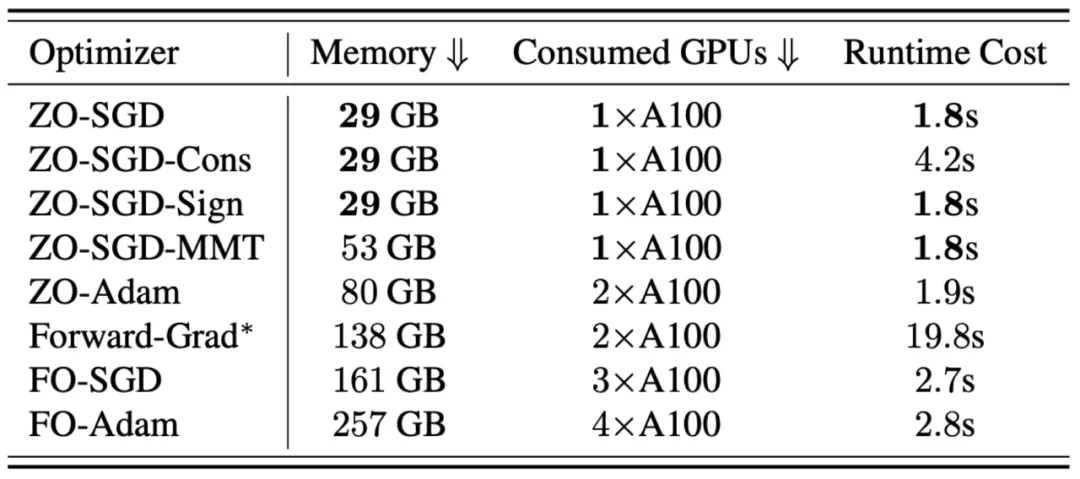
以 OPT-13B 模型在 MultiRC 数据集上微调为例，作者还进一步对比分析了不同零阶和一阶优化器的内存与时间成本。如下表所示：首先，从内存效率的角度看，ZO-SGD、ZO-SGD-Cons 和 ZO-SGD-Sign 显示出了类似的高内存效率，只需要一个 A100 GPU 来进行大型语言模型的微调。这并不令人惊讶，因为这些零阶优化器采用相对简单的优化步骤，主要依赖于零阶梯度估计器 RGE 的利用。其次，Forward-Grad 似乎是零阶优化方法在内存效率方面超过一阶方法的临界点（例如与 ZO-Adam 相比）。最后，与一阶方法相比，零阶优化每次迭代的运行时间成本降低了约 41.9%（以 ZO-SGD 与 FO-SGD 为例）。

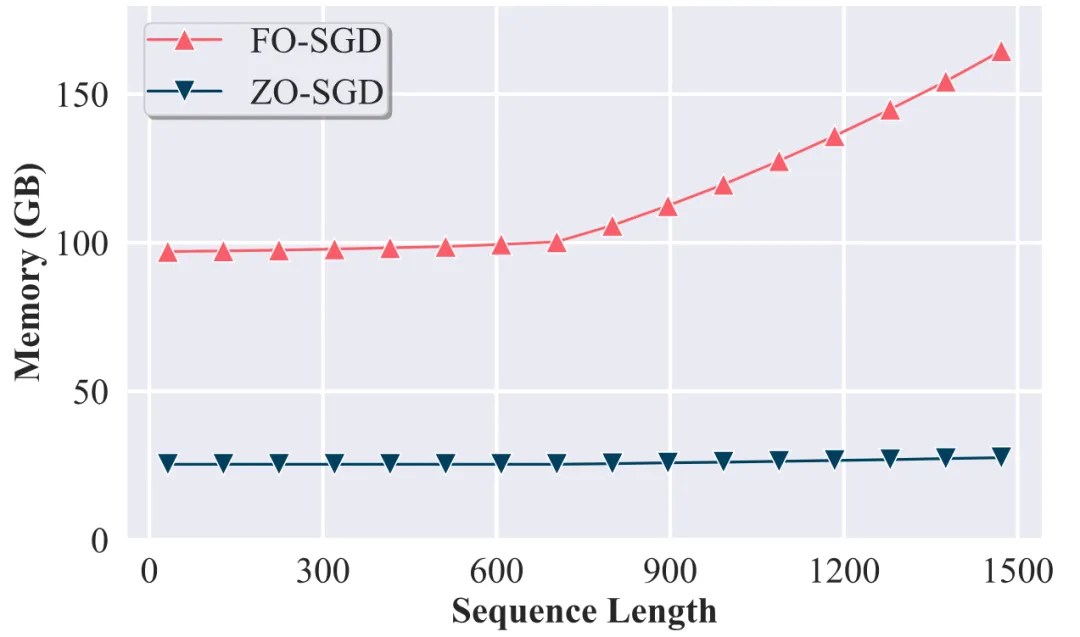
作者进一步深入比较了 ZO-SGD 与 FO-SGD 在不同序列长度下的内存效率。可以看到，ZO-SGD 的内存消耗保持一致，因为其峰值内存消耗仅由模型参数大小决定，相比之下，随着序列长度的增加，FO-SGD 的峰值内存消耗先保持不变，然后开始增加。因此，在长上下文长度的设置中，ZO-SGD 将展示出更好的内存效率优势。具体的内存理论值和实验值可参见原论文。

三种改进算法用以增强零阶优化器

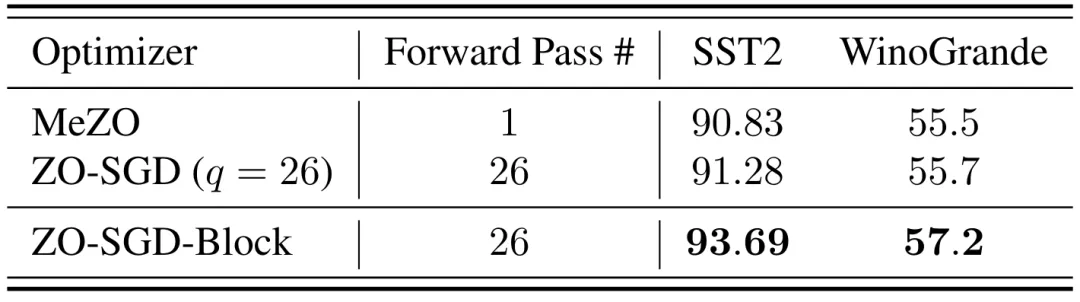
零阶优化器在应用于 LLM 时收敛效率受限，主要是因为它们在梯度估计上的方差较大。为了进一步增强零阶优化器，作者从降低梯度估计方差的角度入手，提出了三种进阶算法，包括：分块零阶微调（block-wise ZO fine-tuning）、零阶和一阶混合微调（hybrid ZO and FO fine-tuning）、引入稀疏性的零阶梯度估计（sparsity-induced ZO gradient estimation）。 **分块零阶微调（Block-wise ZO fine-tuning）**此方法的主要出发点在于，如果零阶优化器在估计梯度时，对 LLM 中参数分块分别进行扰动，通过降低问题规模的方式来见效每次对梯度估计的方差，从而改进优化性能。这种方法的优点体现在能够对模型梯度进行更准确的估计，但是完成一次梯度估计所需要的前向传播的次数会增加。例如，OPT-1.3B 可以分成 26 个参数块（24 个 Transformers 层、嵌入层和 LM 分类头），那么零阶优化器每次计算模型梯度时就会计算 26 次前向传播。为了公平比较 ZO-SGD 和 ZO-SGD-Block，作者还比较了另一种 ZO-SGD 变体的性能，该变体每次对完整的模型进行参数扰动，并将多次扰动后的梯度估计求平均（例如 OPT-1.3B 的 26 次），以此来保证比较时的前向传播次数相同。OPT-1.3B 上实验结果表明，ZO-SGD-Block 大幅超越了两种 ZO-SGD。

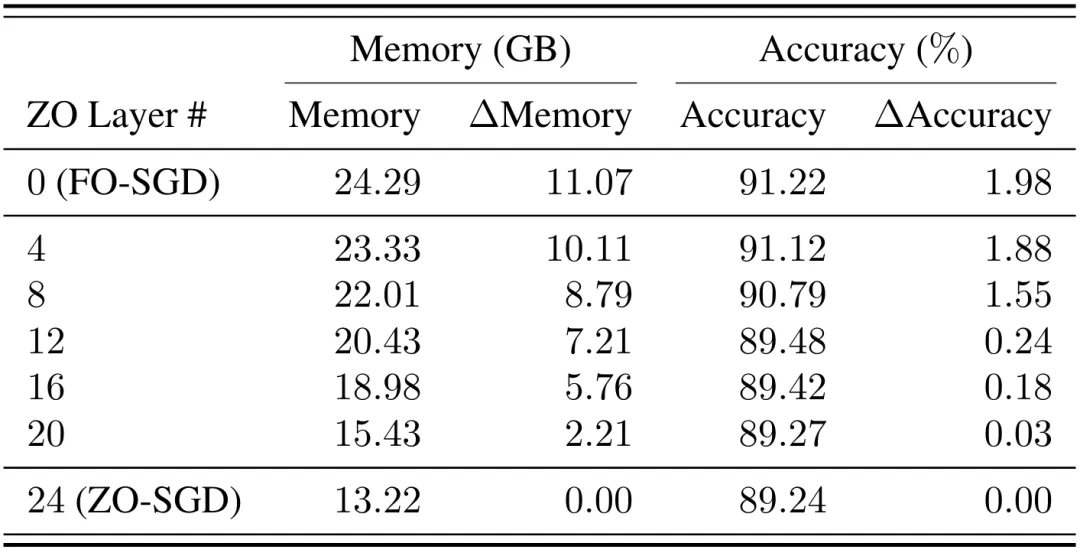
**零阶和一阶混合训练（Hybrid ZO and FO fine-tuning）**反向传播（BP）从深层至浅层神经网络依次计算权重梯度。由于零阶优化器在内存占用上有远超传统一阶优化器的优势，但一阶优化器的性能往往更好。因此，采用零阶和一阶优化器的结合将达到一种内存使用和性能之间的平衡（trade-off）。具体而言，对于较深层次网络，可以利用一阶优化器通过反向传播精确计算梯度；对于浅层网络，则可以通过零阶优化器进行梯度估算。实验结果表明，在浅层部分（例如 OPT-1.3B 的前 8/24 层）采用零阶优化器，而在剩余的深层部分使用一阶优化器，可以在节约大约三分之一的显存的同时，达到与完全使用一阶优化器相同的性能水平。

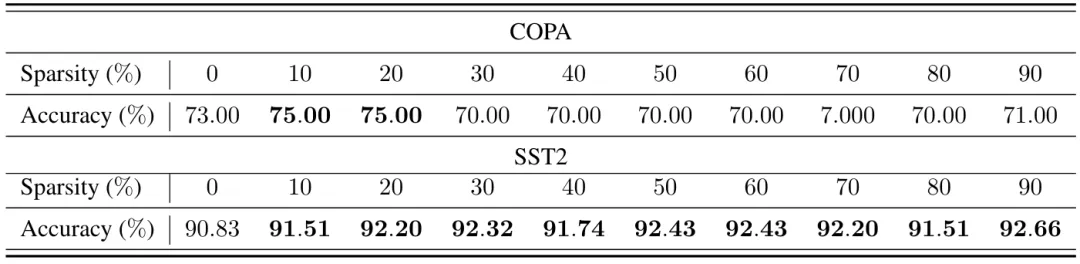
**使用稀疏梯度的零阶优化器（ZO with gradient pruning）**在一阶优化器中，梯度剪裁通常用于加速训练过程；而在零阶优化器中，通过梯度剪裁引入的稀疏梯度可以进一步降低梯度估计的方差，从而提高性能。本文研究了在零阶优化器中应用基于幅值的剪裁策略来获取每一层的稀疏率，然后根据这些稀疏率生成随机的稀疏梯度掩码（mask），并将其应用于随机梯度估计的扰动上。实验结果显示，适度的梯度稀疏性（约 20% 左右）能给零阶优化器带来一定程度的性能提升。

结语

在本文中，我们展示了零阶优化器在大型语言模型微调中的有效应用。通过利用损失差分来近似梯度，零阶优化方法避免了反向传播和激活存储的需求，极大地节省了内存资源。我们通过扩大已有的研究范围，将不同的零阶优化方法、任务类型及评估指标容纳到了本次评测中，进行了首次系统的零阶优化技术基准研究。我们的研究不仅揭示了这些方法在精度和效率方面的表现，还深入探讨了任务对齐和前向梯度的关键作用。利用这些实验分析，我们提出了诸如分块优化、零阶与一阶混合训练、梯度稀疏化等技术，以进一步增强基于零阶优化的大模型微调。这些改进技术旨在在保持内存效率的同时，提高微调的准确性。 我们坚信，这些发现和技术的应用可以大力降低大模型研究对硬件资源的要求，使得大模型微调在低端 GPU 也成为可能，从而进一步推动学术研究并在工业界产生实际而有价值的影响。我们鼓励广大研究人员和技术开发者关注我们的研究成果，并探索更多利用 ZO 优化的可能性。未来的研究将继续探索这一领域的深层问题，以解锁 LLM 微调中的更多潜力。 了解更多内容请参考论文与 GitHub 仓库，获取更多信息和资源。 Reference:[1] Liu, et al,. "A primer on zeroth-order optimization in signal processing and machine learning." IEEE Signal Processing Magazine 37, no. 5 (2020): 43-54.[2] Malladi, et al., “Fine-Tuning Language Models with Just Forward Passes.” NeurIPS’ 2023.[3] Liu, et al., “A Primer on Zeroth-Order Optimization in Signal Processing and Machine Learning.” IEEE Signal Processing Magazine.[4] Ghadimi, et al., “Stochastic First- and Zeroth-order Methods for Nonconvex Stochastic Programming.” [5] Liu, et al., “signSGD via Zeroth-Order Oracle. ” ICLR’ 2019.[6] Huang, et al., “Accelerated Zeroth-Order and First-Order Momentum Methods from Mini to Minimax Optimization.” JMLR’ 2022. [7] Kim, et al., “Curvature-Aware Derivative-Free Optimization.”[8] Chen, et al., “ZO-AdaMM: Zeroth-Order Adaptive Momentum Method for Black-Box Optimization.”[9] Baydin, et al., “Gradients without Backpropagation.”