【ICML2024】更快的自适应去中心化学习算法

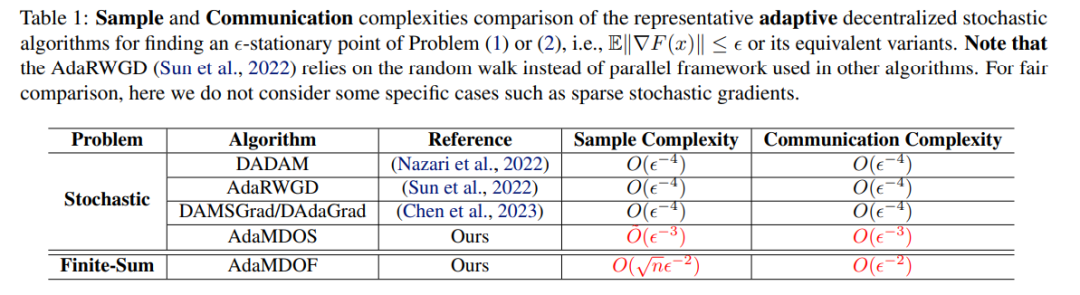
近年来，去中心化学习因其在实现简便性、系统鲁棒性和数据隐私方面的优势而在机器学习中受到越来越多的关注。同时，自适应梯度方法在许多机器学习任务中（如神经网络训练）表现出卓越的性能。尽管已有一些工作专注于研究具有自适应学习率的去中心化优化算法，但这些自适应去中心化算法仍然面临高样本复杂度的问题。为填补这些空白，我们提出了一类更快的自适应去中心化算法（即AdaMDOS和AdaMDOF），分别适用于分布式非凸随机优化和有限和优化。此外，我们为这些方法提供了坚实的收敛性分析框架。特别是，我们证明了AdaMDOS在求解非凸随机优化的ϵ-平稳解时，具有接近最优的样本复杂度O˜(ϵ⁻³)。同时，我们的AdaMDOF在求解非凸有限和优化的ϵ-平稳解时，达到了接近最优的样本复杂度O(√nϵ⁻²)，其中n表示样本大小。据我们所知，AdaMDOF算法是首个针对非凸有限和优化的自适应去中心化算法。一些实验结果展示了我们算法的高效性。