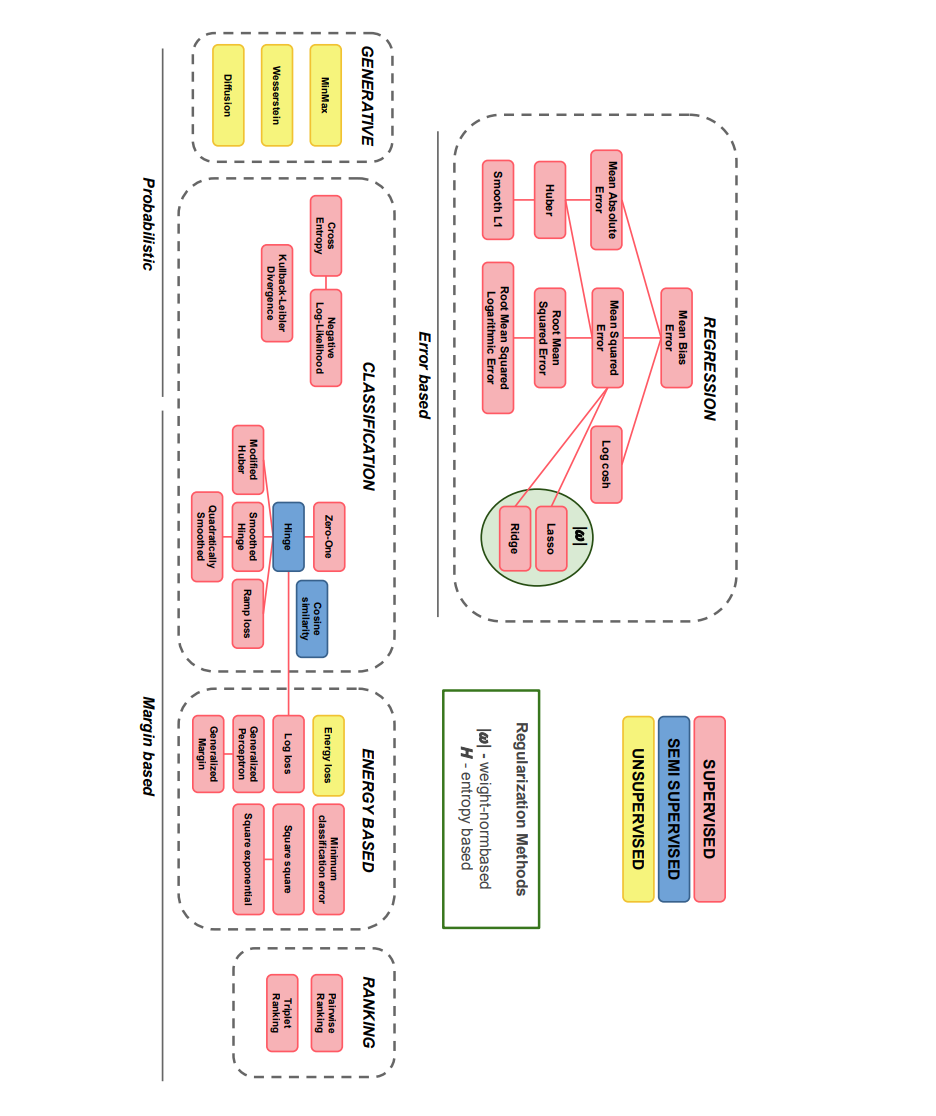
大多数最先进的机器学习技术都围绕着损失函数的优化。因此,定义适当的损失函数对于成功解决该领域的问题至关重要。本文对不同应用中最常用的损失函数进行了调研,分为分类、回归、排序、样本生成和基于能量的建模。**总的来说,引入了33个不同的损失函数,并将它们组织成一个直观的分类。**每个损失函数都有一个理论支持,我们描述了它的最佳使用场合。本综述旨在为初学者和高级机器学习从业者提供最基本的损失函数的参考。
https://www.zhuanzhi.ai/paper/3e64149d97a56cf39dd70626539f829c
1. 引言
**在过去的几十年里,人们对机器学习的兴趣呈爆炸式增长[52,76]。该领域的重点是算法的定义和应用,这些算法可以在数据上进行训练,以建模基础模式[11,73,77,88]。机器学习方法可以应用于许多不同的研究领域,包括生物医学[59,84,95,126],自然语言理解[22,83],[97]异常检测[17],图像分类[71],数据库知识发现[32],机器人学习[3],在线广告[86],时间序列预测[13],脑机接口[78]等[98]。**为了训练这些算法,有必要定义一个目标函数,它可以给出算法性能的标量度量[77,116]。然后可以通过优化目标函数的值来训练它们。在机器学习文献中,这种目标函数通常以损失函数的形式定义,当它们最小化时是最优的。损失函数的确切形式取决于待解决问题的性质、可用的数据和被优化的机器学习算法的类型。因此,寻找合适的损失函数是机器学习中最重要的研究工作之一。随着机器学习领域的发展,许多不同的损失函数被提出。因此,总结和理解它们是非常有用的。然而,很少有工作试图在整个领域这样做[119]。文献中现有的损失函数综述要么缺乏一个良好的分类来构建不同的损失并将其上下文化,要么特别关注机器学习应用的一个特定子集[49,117]。也没有任何一个来源将最常用的损失函数放在相同的形式设置中,列出每个函数的优点和缺点。
**因此,本文致力于建立一个适当的损失函数分类,展示每种技术的优缺点。我们希望这对新用户有用,他们希望熟悉机器学习文献中最常见的损失函数,并找到适合他们试图解决的问题的损失函数。**我们也希望这个总结对高级用户来说是有用的综合参考,使他们能够快速找到最好的损失函数,而不必广泛搜索文献。此外,这可以帮助研究人员找到进一步研究的可能途径,或了解在哪里放置他们提出的任何新技术。例如,他们可以通过这项调研来了解他们的新提案是否符合我们提出的分类方法,或者是否属于一个全新的类别,也许可以以新颖的方式组合不同的想法。总的来说,我们包含了33个最广泛使用的损失函数。在这项工作的每个部分中,我们根据它们可用于的任务的广泛分类对损失进行细分。每个损失函数都将被数学定义,并列出其最常见的应用,突出其优点和缺点。这项工作的主要贡献可以在图1所示的分类中找到。首先,根据每个损失函数的具体任务进行划分:回归、分类、排序、样本生成和基于能量的建模。按其可应用的学习范式类型将它们分为有监督和无监督。最后,我们根据它们所基于的底层策略对它们进行分类,例如它们是否依赖于概率形式化,或基于预测和实际值之间的误差或间隔。
**这项工作的组织如下:**在第2节中,我们提供了损失函数的正式定义并介绍了分类方法。在第3节中,我们将介绍用于降低模型复杂度的最常用正则化方法。在第4节中,我们描述了回归任务和用于训练回归模型的关键损失函数。在第5节中,我们将介绍分类问题和相关的损失函数。在第6节中,我们介绍了生成模型及其损失。第7节介绍排序问题及其损失函数,第8节介绍基于能量的模型及其损失。最后,我们在第9节得出结论。
图1所示。拟议的分类法。确定了损失函数应用于的五个主要任务,即回归、分类、排序、生成样本(生成)和基于能量的任务。我们用不同的颜色指定学习范式的类型,每个损失函数从监督到无监督。最后,在每组损失下阐述了优化它们的基本策略,即基于间隔、基于概率和基于误差的策略。
正则化方法
正则化方法可以应用于几乎所有的损失函数。它们用于降低模型复杂度,简化训练模型,减少其过拟合训练数据的倾向[5,30,61]。模型复杂度,通常由参数的数量及其大小[5,77,79]来衡量。有许多技术属于正则化方法的范畴,其中相当一部分是基于损失函数的增广[30,77]。对正则化的一个直观解释是,它对最终模型的复杂性施加了奥卡姆剃刀。从理论上讲,许多基于损失的正则化技术等价于对模型参数施加某些先验分布。
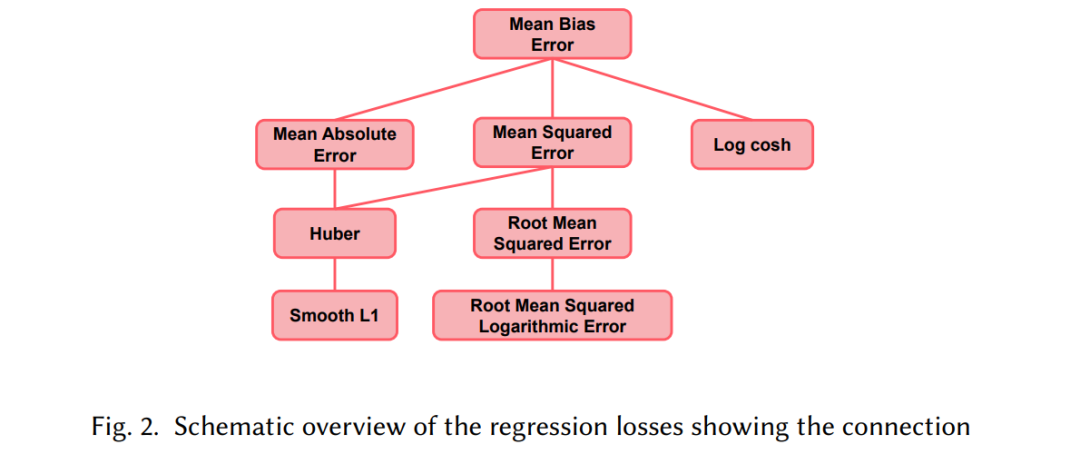
回归损失
回归模型的目的是根据一个或多个预测变量x(自变量)的值来预测连续变量𝑦(因变量)的结果。更准确地说,设𝑓Θ为一个通用模型,参数为Θ,映射自变量x∈{x0,…, x𝑁},x𝑖∈R𝐷转化为因变量𝑦∈R。最终目标是通过最小化损失函数𝐿来估计模型Θ的参数,该参数最接近于拟合数据。
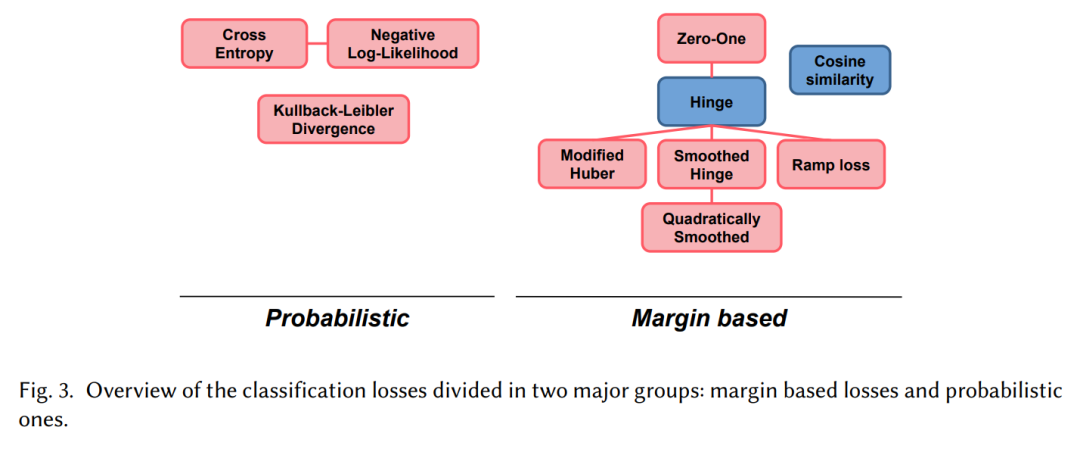
分类损失
分类是监督学习问题的一个子集。目标是将输入x分配给𝐾离散类之一。可以通过最小化损失函数𝐿来训练模型𝑓Θ及其参数Θ来实现这一目标。让𝑓的目标空间离散,并考虑返回输出标签的模型。
生成式损失
近年来,生成模型在理解数据分布的复杂性和能够重新生成数据方面变得特别有用[36,37]。在本节中,如图4所示,我们描述了与生成对抗网络(GANs)和扩散模型相关的损失。然而,生成模型并不局限于这些情况,而是扩展到包括更多的模型。例如,变分自动编码器(VAE)[2,55,87],其中第5.3.2节中描述的KL散度是使用的损失函数。VAE损失的目的是减小原始分布与预测分布之间的差异。其他模型,如像素递归神经网络[113]和实值非体积保持(realNVP)模型[27],在本综述中没有考虑。
排序损失
机器学习可以用来解决排序问题,在信息检索系统中有着重要的工业应用。这些问题通常可以通过使用监督、半监督或强化学习来解决[15,47]。与交叉熵损失或MSE损失等其他损失函数不同,对损失进行排序的目标是预测输入之间的相对距离,而不是学习预测给定输入的标签、值或一组值。这也被称为度量学习。然而,交叉熵损失可以用于top- 1概率排序。在这种情况下,给定所有对象的分数,该模型中一个对象的前一个概率表示它将排名第一的可能性[16]。训练数据的排序损失函数可以高度定制,因为它们只需要一种方法来衡量两个数据点之间的相似性,即相似性分数。例如,考虑一个人脸验证数据集,属于同一个人的照片对将具有较高的相似性分数,而不属于同一个人的照片对将具有较低的分数[118]一般来说,排序损失函数需要对两个(或三个)数据实例进行特征提取,从而返回每个数据实例的嵌入表示。然后可以定义一个度量函数来度量这些表示之间的相似性,如欧几里得距离。最后,对特征提取器进行训练,以便在输入相似时为两个输入生成相似的表示,在输入不相似时生成距离较远的表示。与第6节类似,两两排序损失和三重排序损失均以一般形式呈现,如图5所示。根据所选择的度量函数确定损失函数的属性(CONT、DIFF等)。
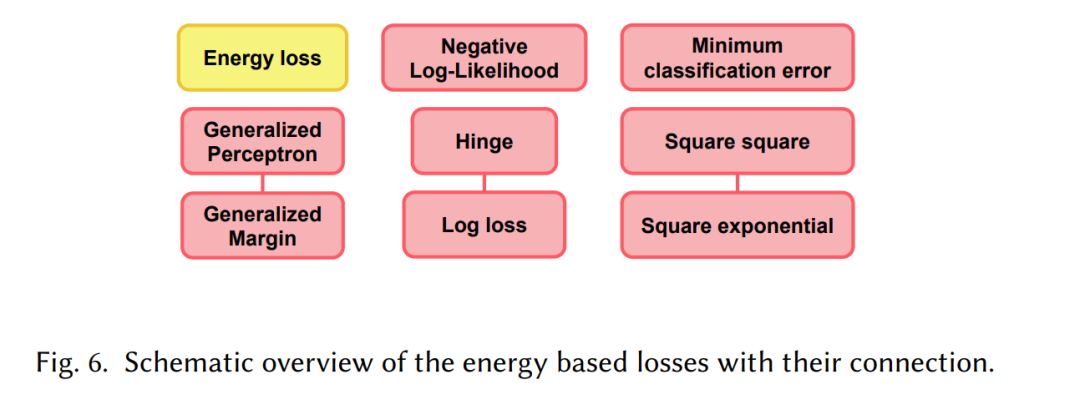
基于能量的损失
基于能量的模型(energy - based Model, EBM)是一种使用标量能量函数来描述模型变量之间依赖关系的概率模型**。