【阿姆斯特丹博士论文】等变和坐标无关的卷积网络，528页pdf

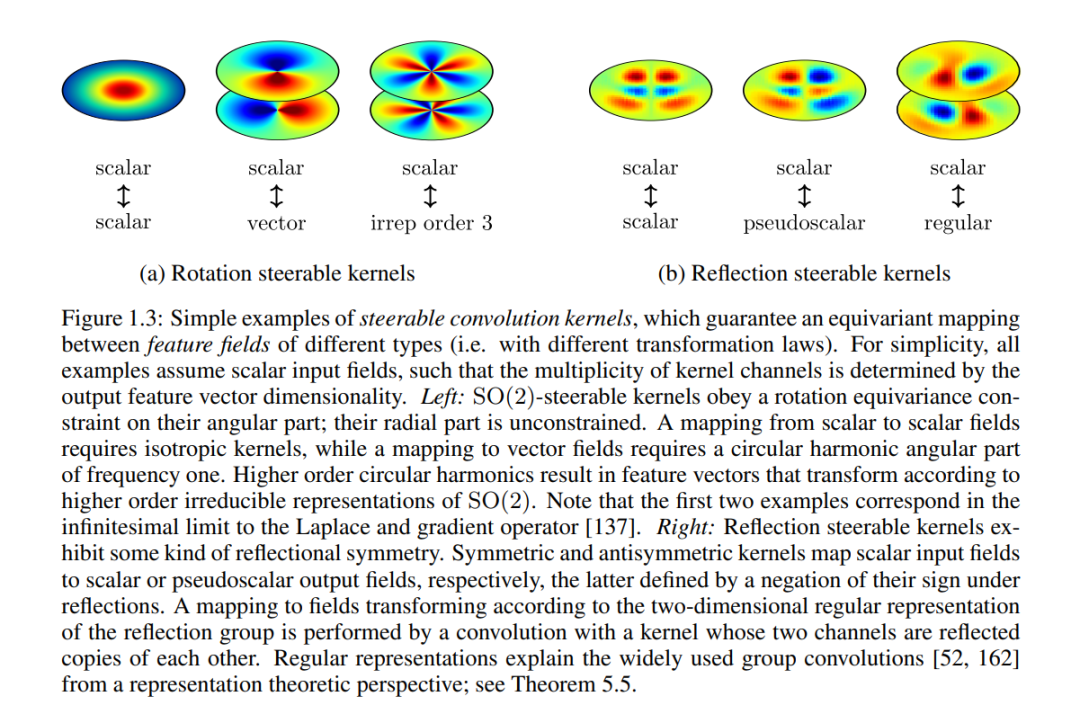
在这篇论文《等变与坐标独立卷积网络》中，我们为处理图像、音频或视频等空间结构化数据开发了一种人工神经网络的规范理论。标准的神经网络架构用于此类数据的是卷积网络，其特点是位置无关的推理。卷积网络能够将其学习内容在空间位置上进行泛化，与非卷积模型相比，卷积网络在数据效率和稳健性方面具有显著优势。这一特性在医疗成像等训练数据稀缺的领域尤为重要。卷积网络对空间位置的独立性通过其平移群等变性形式化地体现出来，即其性质是与输入信号的平移相交换。我们表明，卷积网络设计不仅足以实现平移等变性，实际上是一个必要条件——因此，通过要求模型的等变性可以推导出卷积。本文的第一部分利用这一见解定义了在更大对称群下等变的广义卷积网络。此类模型可以对额外的几何变换进行泛化推理，例如图像中模式的旋转或反射。我们通过实验证明，与传统卷积网络相比，它们在数据效率、收敛速度和最终性能方面显著提升。我们的公开实现广泛应用于研究社区。在第二部分中，我们进一步扩展卷积网络以处理黎曼流形上的信号。除了平坦的欧几里得图像外，这一设定还包括例如地球表面的全球天气模式等球面信号，或动脉壁或大脑皮层等一般表面上的信号。我们表明，如果要求网络推理具有坐标独立性，则流形上的卷积核必须在局部规范变换下保持等变。结果得出的坐标独立网络被证明相对于流形的全局对称性（等距变换）是等变的。我们的目标不是为狭窄的应用领域提出另一个等变网络设计，而是设计一个统一的卷积网络数学框架。论文的最后一部分展示了我们关于卷积网络的微分几何公式的普遍性，证明其能够解释文献中大量的等变网络架构。

在过去的几十年中，计算方法在广泛的应用中变得越来越重要。传统上，这些底层算法是硬编码的，即程序员明确指定算法如何处理数据。虽然这种方法适用于输入和输出空间严格控制的任务，但对于诸如计算机视觉或语音识别等更复杂的任务来说，这种方法很快变得不可行，因为要处理的数据表现出相当大的变异性。机器学习算法旨在通过用适应性模型代替硬编码算法来解决这一问题，这些模型根据数据进行调整。 虽然机器学习范式减轻了程序员硬编码算法的负担，但随着任务复杂性的增加，问题依然存在——这在这里表现为对训练数据需求的增加，而这也很快变得不可行。大量的机器学习研究集中于通过将关于学习任务的先验知识纳入机器学习模型来缓解这一问题。其中一个最成功的方法是群等变模型。等变学习算法将学习任务的对称性或不变性直接硬编码到模型的空间中进行优化，这大大提高了数据效率。

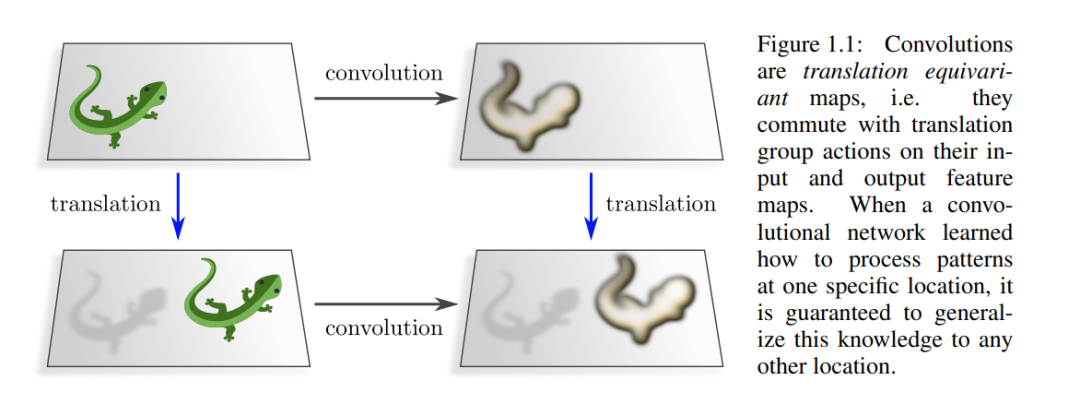
这种设计原则的一个典型例子是卷积神经网络 (CNN) [175, 166]。传统的卷积神经网络处理欧几里得空间上的信号，例如图像，并通过具有空间共享突触权重的局部神经连接来利用其空间结构。由于相同的卷积核（神经连接）应用于空间中的每个点，卷积是平移等变映射——其输入的任何平移都会导致输出的相应平移，如图1.1所示的交换图表所示。因此，卷积网络自动将其推理泛化到空间位置上，也就是说，当某个模式在不同位置重新出现时，它们不需要显式地重新学习如何处理该模式。由于其数据效率和稳健性得到了改进，卷积网络如今已成为处理空间结构化数据（如音频、图像、体积信号或视频）的事实标准模型。 鉴于传统欧几里得卷积神经网络的显著经验成功，人们对扩展卷积模型的兴趣很大：

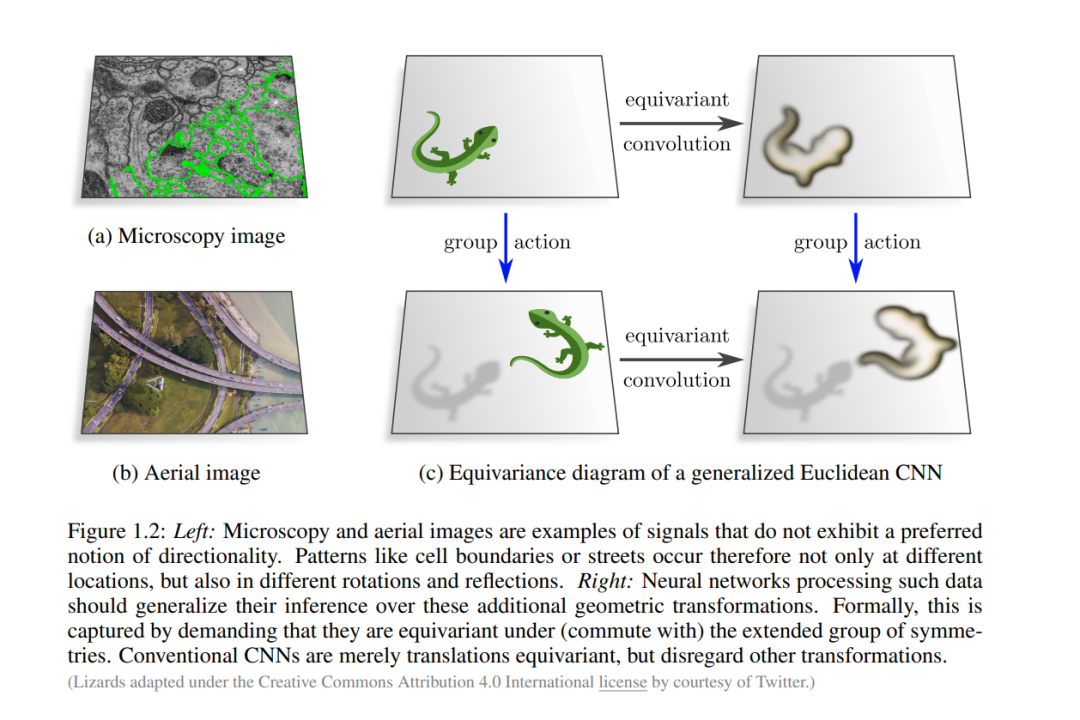
1. 在更大的对称群下具有等变性，参见图1.2
2. 处理更一般域上的信号，参见图1.4 本工作提出了一种黎曼流形上的等变与坐标独立卷积网络的规范理论，解决了这两点。为了提供一个简单的入门，并遵循历史发展，第一部分首先介绍了欧几里得空间上的等变卷积（“可转向CNN”），然后第二和第三部分开发了完整的微分几何公式。第四部分通过解释文献中的大量卷积网络作为坐标独立卷积网络的具体实例，展示了这种公式的普遍性；参见第293页的表15.1。 本介绍部分的其余部分相应地分为欧几里得和黎曼公式的坐标独立卷积网络及其应用的高层次概述。详细的内容大纲见第15页。前言部分提供了一个较少技术但更具视觉的介绍和动机。