大模型数学推理数据合成相关方法

© 作者｜王家鹏 机构｜中国人民大学研究方向｜大语言模型 数学推理能力作为大模型的核心能力之一，近年来受到学术界广泛关注，其性能表现也取得了显著提升。研究表明，高质量的训练数据是提升大语言模型数学推理能力的关键基础。然而，由于数学领域专业标注成本高昂、优质监督数据稀缺，大规模高质量数据集的获取成为制约模型性能提升的主要瓶颈。为突破这一限制，研究者们提出了多种创新性的数据合成方法，这些方法不仅有效解决了数据稀缺问题，还为模型性能提升提供了新的思路。本文将介绍大模型数学推理数据合成的几种相关方法和研究工作。

文章也同步发布在 AI Box 知乎专栏（知乎搜索 AI Box 专栏），欢迎大家在知乎专栏的文章下方评论留言，交流探讨！

一、增强现有数据

MetaMath: Bootstrap Your Own Mathematical Questions for Large Language Models

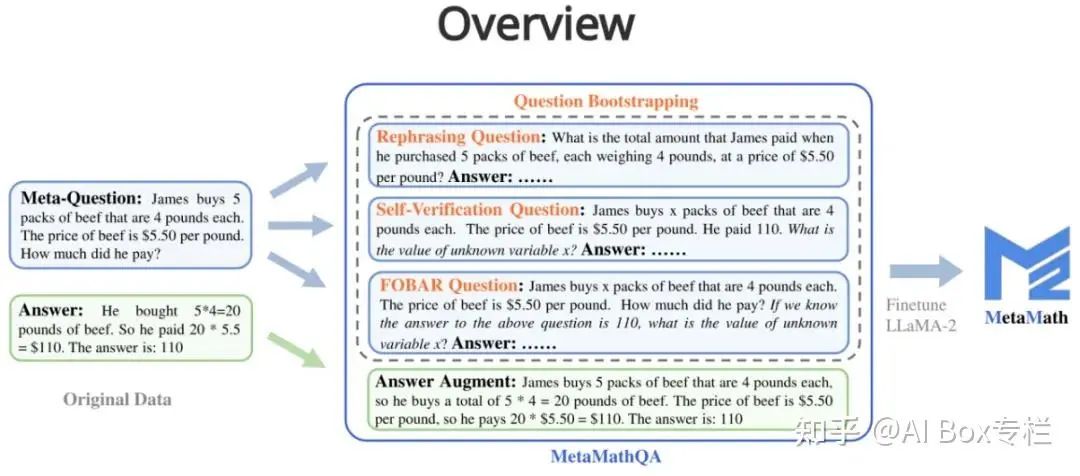
MetaMath通过重写技术来增加训练数据集中的数学问题多样性，并在新的数据集MetaMathQA上微调模型。重写包括以下几种：

1. Answer Augmentation (答案增强)：给定问题，通过大语言模型生成能得到正确结果的思维链作为数据增广。
2. Rephrasing Question (问题改写增强)：给定元问题，通过大语言模型重写问题并生成得到正确结果的思维链作为数据增广。
3. FOBAR Question (FOBAR 逆向问题增强)：给定元问题，通过掩码条件中的数字为 x，给定原有答案并反推 x 来产生逆向问题，并基于该逆向问题生成正确的思维链过程来进行数据增广（反推样例：“If we know the answer to the above question is 110, what is the value of unknown variable x?”）。
4. Self-Verification Question (Self-Verification 逆向问题增强)：在 FOBAR 的基础上，通过大语言模型改写逆向问题部分为陈述的语句来进行数据增广（改写样例：“How much did he pay?” (with the answer 110) 被改写成 “He paid 110”）。 实验表明，MetaMathQA提高了思维链数据的质量和多样性，显著提升了模型准确率。相比之下，简单地使用答案增强会导致明显的准确率饱和。

MuggleMath: Assessing the Impact of Query and Response Augmentation on Math Reasoning

论文试图回答以下三个问题：

1. 哪些数据增强策略更有效？ 论文研究了不同的数据增强策略，以确定哪些方法在提升数学推理任务中最为有效。
2. 增强数据量与模型性能之间的扩展关系是什么？ 论文探讨了增加增强数据量对模型性能的影响，并试图找到它们之间的量化关系。
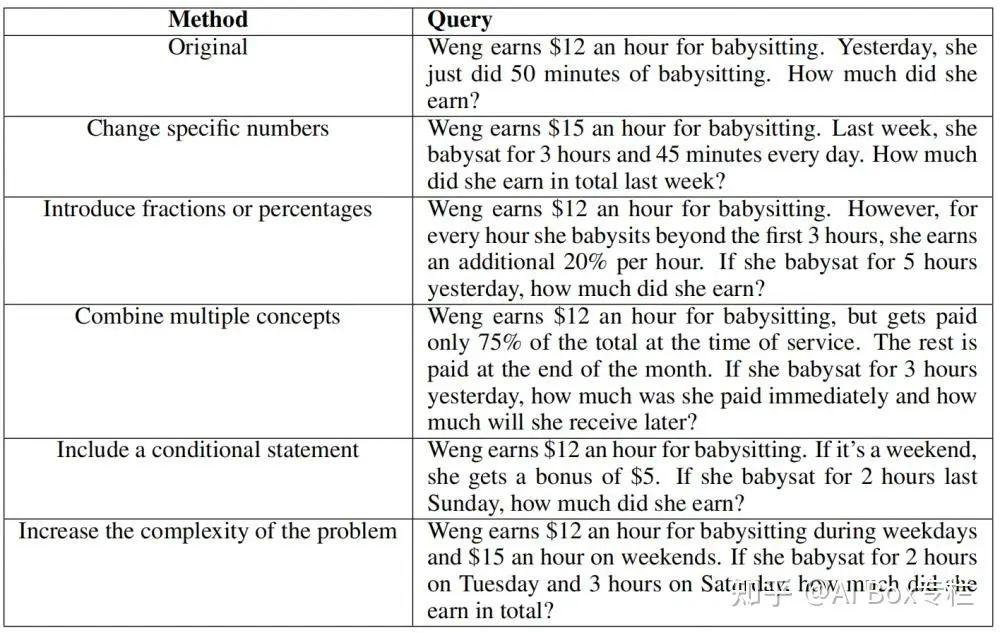
3. 数据增强是否能促进模型对领域外数学推理任务的泛化？ 论文考察了通过数据增强训练得到的模型是否能够泛化到不同的数学推理领域。 通过对原有问题进行改写（后文称作问题增强），并通过对改写后的新问题采样不同的回答（后文称作回复增强），文章获得了新的增强数据集。 问题增强的改写方式为根据人类知识设计的五条规则：Change specific numbers; Introduce fractions or percentages; Combine multiple concepts; Include a conditional statement; Increase the complexity of the problem. 回复增强则是通过对 GPT-3.5 和 GPT-4 推理时的温度系数进行设置，获得多样化的推理路径。

作者发现不同问题增强的方式都可以对不同尺度的 LLaMA 模型有效的增强，但是 Increase complexity 这种方式的相对效果最好。随着数据增强产生的问题-答复增加时，这些模型在 GSM8K 的测试集上的准确率也保持增长，而这个关系可以用对数线性关系表示；但仅仅做回复增强则会出现性能增长上限。最后，作者发现不论是问题增强还是回复增强对于领域内的数学推理能力提升都是巨大的，但是对于其他领域的数学问题的是否同样有效是一个值得探究的问题：例如相对于GSM8K数据增强在本基准上的性能提升，在 MATH 上的提升则不稳定且不明显。

WizardMath: Empowering Mathematical Reasoning for Large Language Models via Reinforced Evol-Instruct

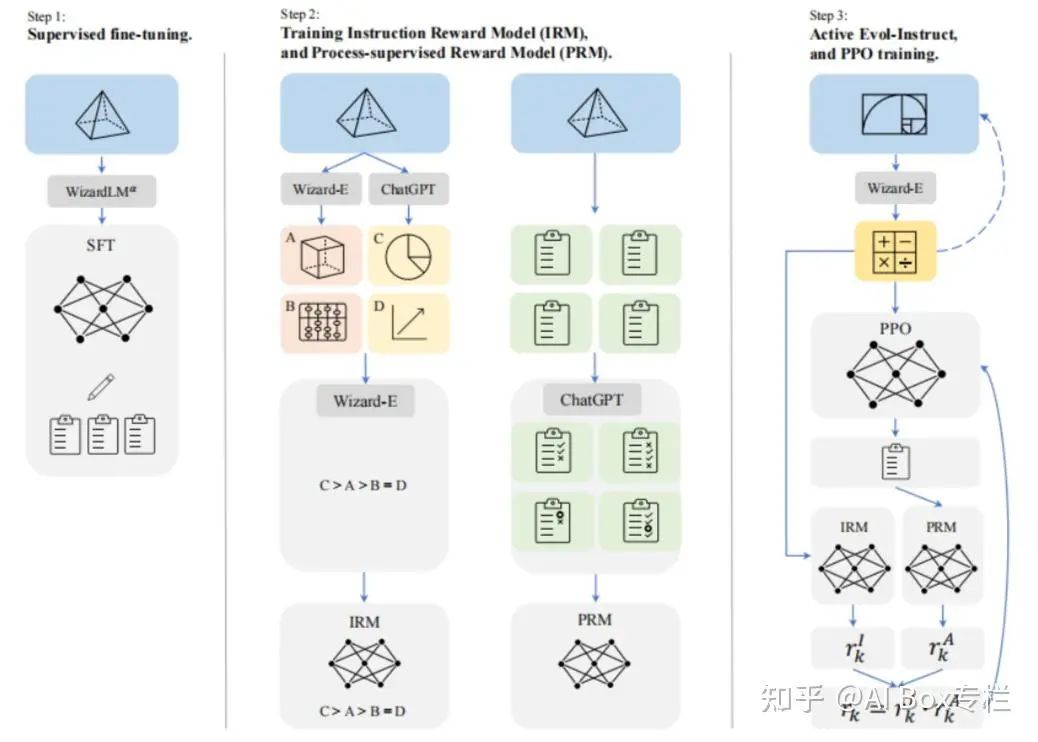
受WiazrdLM提出的Evol-Instruct方法及其在WizardCoder上的有效应用的启发，本工作试图合成具有各种复杂性和多样性的数学指令，以增强大语言模型的数学能力。具体而言，本文采用了包含两条进化线的新范例。

1. 下行演化：通过降低问题难度来改进指导，例如将高难度问题改为低难度问题，或者产生一个新的、与原题不同的简单问题。
2. 上行演化：源自原始的Evol-Instruct方法，通过增加限制条件、具体化和增加推理来深化和生成新的更难的问题。 作者训练了两个奖励模型来分别预测指令的质量和答案中每一步的正确性，并最终进行强化学习PPO训练。

以上合成数据方法通常基于有限的预设问题和知识生成新问题。然而，随着数据规模的扩大，这种生成方式逐渐暴露出局限性，导致生成的问题趋于重复和同质化，降低了数据的多样性。结果是，随着训练数据的不断扩展，模型性能难以持续提升，形成了扩展瓶颈。研究人员逐渐转向根据知识点/种子数据/直接合成大规模新问题。

二、直接合成新问题

Key-Point-Driven Data Synthesis with its Enhancement on Mathematical Reasoning

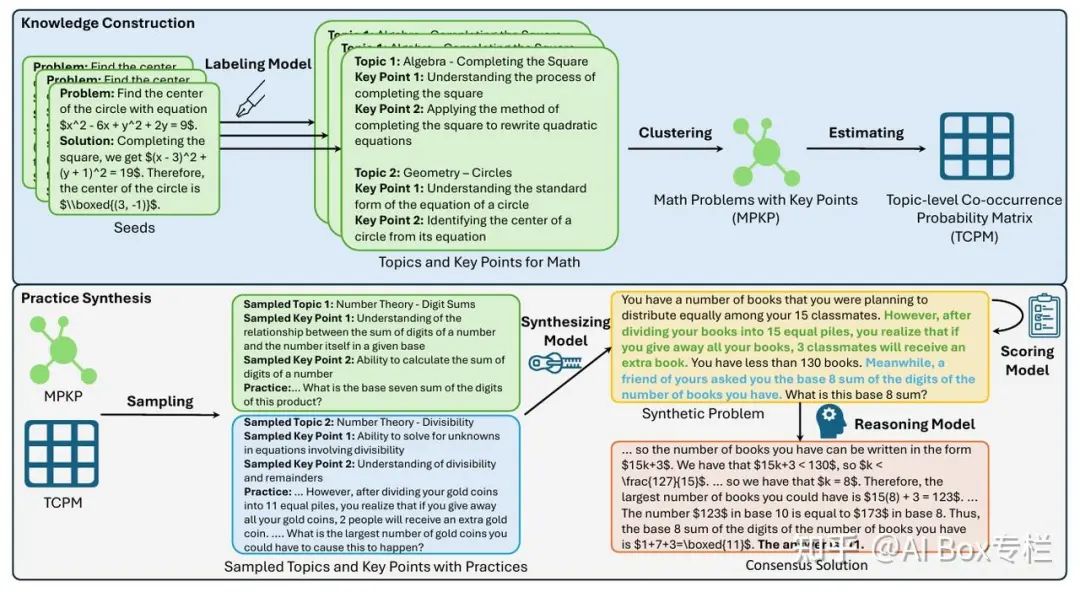
这篇工作提出了关键点驱动的数据合成（KPDDS）框架，这是一种新颖的数据合成方法。研究利用来自真实数据源的关键点和示例对来合成问题-答案对，确保了生成具有严格的质量控制和可扩展性的新问题整个框架包括以下几个步骤：1）知识提取与构建；2）通过质量评估合成问题；3）通过共识评估合成答案；4）问题-答案对构建。

1. 知识提取与构建：使用标签模型（Labeling Model）从种子问题提取与数学问题相关的主题和关键点（KPs）。通过聚类算法对提取的KPs进行去重和整合，确保每个聚类包含至少10个KPs，从而构建了包含多个主题和KPs的数学实践数据集（MPKP）。计算MPKP数据集中主题对的共现频率，构建TCPM，用于理解数据集中主题对的出现频率和分布情况。
2. 通过质量评估合成问题：利用TCPM作为指导，从MPKP中随机采样多个主题和KPs，形成基础信息集，用于生成新的问题。使用GPT-4根据这些信息集生成新的问题，并进行质量评估，确保问题符合预设的关键点且无逻辑或事实错误。
3. 通过共识评估合成答案：采用少样本策略和核采样为问题生成多种可能的解答。并通过投票机制，从多个生成的解答中整合出共识解答，确保答案的正确性和可靠性。
4. 问题-答案对构建：为了增加数据的数量和多样性，对共识的问答对进行了问题改写。因此，对于每个唯一的问题，我们生成了一系列改写的问题和一组答案，尽管它们具有相同的最终答案，但其推理过程是不同的。通过随机配对这些问题和答案，为每个唯一的问题生成了30对。通过筛选机制，保留质量最高的问答对，构建最终的合成数据集KPMath。

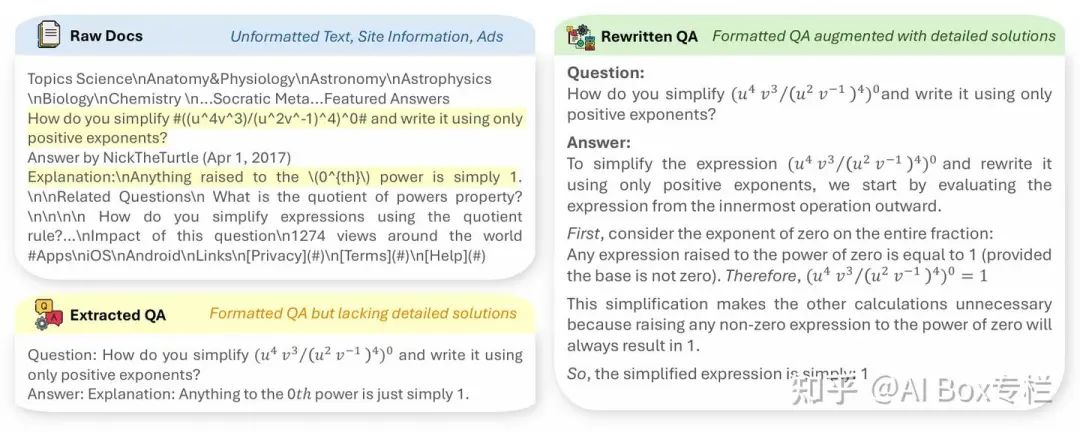
MAmmoTH2: Scaling Instructions from the Web

本文提出了一种范式，从预训练的网络语料库中高效地收集1000万个自然存在的指令数据，以增强LLM推理。该方法使用一个三步流程：1) 检索相关文档，2) 提取指令-响应对，以及 3) 使用开源LLMs精炼提取。

1. 检索相关文档：通过爬取几个测验网站创建一个多样化的种子数据集。论文使用这些种子数据训练一个fastText模型，并用它从Common Crawl中召回文档。使用GPT-4根据根URL对召回的文档进行修剪。通过这一步骤，论文获得了1800万份文档。
2. 提取指令-响应对：论文利用开源LLM如Mixtral从这些文档中提取问答对，产生大约500万个候选问答对。
3. 精炼提取：提取后，进一步采用Mixtral-8x7B和Qwen-72B来优化这些候选问答对。这一优化操作旨在去除无关内容，修正措辞，并为候选问答对补充缺失的解释。这一优化操作对于保持挖掘问答对的质量至关重要。 最终，论文通过这些步骤收获了总计1000万个指令-响应对。与现有的指令微调数据集不同，论文的WEBINSTRUCT数据集完全是从网络挖掘获得的，而无需任何人工众包或GPT-4蒸馏。

JiuZhang3.0: Efficiently Improving Mathematical Reasoning by Training Small Data Synthesis Models

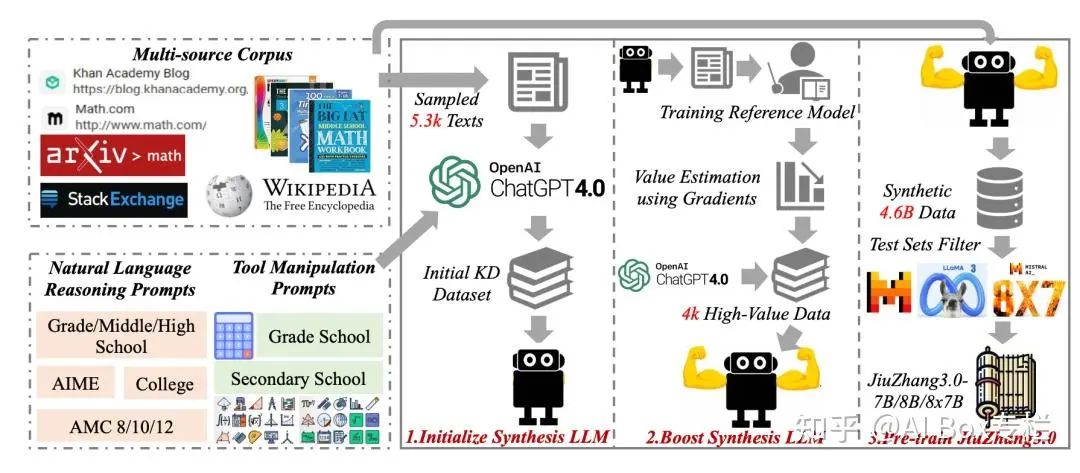
论文通过提出一个高效的方法来解决提升大型语言模型数学推理能力的问题，核心是训练一个小型的LLM根据种子数据来合成高质量的数学问题。JiuZhang3.0的数据合成流程包含以下关键阶段：

1. 构建多源语料库：考虑不同类型的数据，如网页、书籍、论文、问答数据和维基百科等，以构成丰富的数学相关多源语料库。
2. 初始化数据合成模型：首先，通过训练一个小型的LLM，使用知识蒸馏（KD）数据集来模仿GPT-4的数据合成能力。这个KD数据集由一系列手工制作的提示、随机抽样的数学相关文本以及GPT-4生成的相应数学问题和解决方案组成。
3. 提升数据合成模型：在初始化之后，通过使用高价值的KD数据来进一步提升数据合成LLM的能力。这里采用了基于梯度的方法来估计每个合成实例对下游数学相关任务的影响力，并选择排名最高的实例来更新KD数据集，以便重新训练数据合成LLM。 合成数据用于预训练JiuZhang3.0：使用数据合成模型基于多源语料库生成大量的数学问题和解决方案，这些合成数据用于预训练JiuZhang3.0模型。

Unleashing Reasoning Capability of LLMs via Scalable Question Synthesis from Scratch

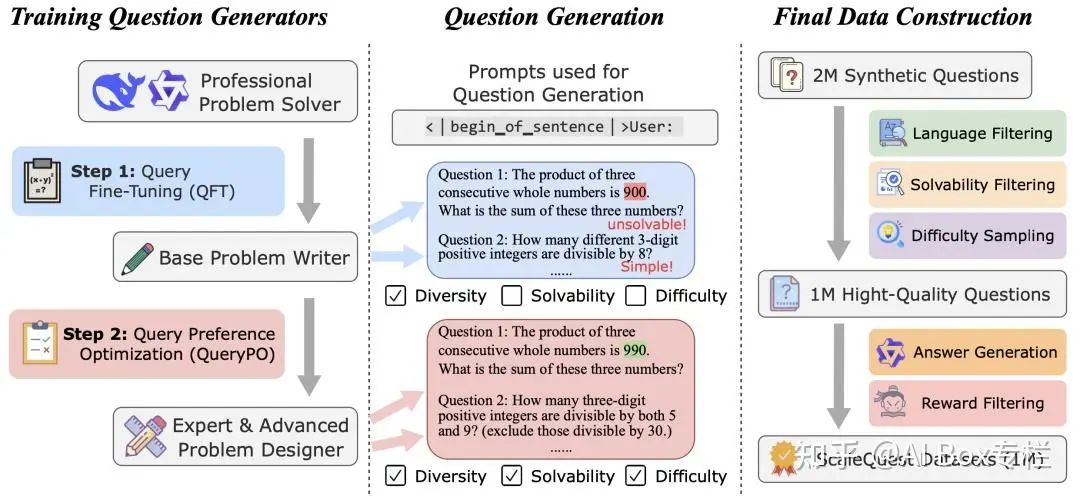
ScaleQuest首先通过QFT和QPO训练出一个问题生成器（仅仅给模型提供一个“ ”词元就可以让模型逐词生成一个问题，和 Magpie类似），然后利用这些生成器进行开放式问题采样，并对生成的问题进行进一步筛选，最终基于筛选出的高质量问题生成相应的解答。

1. 问题微调 (Question Fine-Tuning, QFT) 为了激活模型的问题生成能力，首先进行问题微调（QFT），即使用一小部分问题对现有模型进行训练。基于DeepSeekMath-7B-RL和Qwen2-Math-7B-Instruct，使用了来自GSM8K和MATH训练集的约15,000道问题训练了两个问题生成器。
2. 问题偏好优化（Question Preference Optimization, QPO） 我们进一步通过偏好微调（QPO）优化了这两个问题生成器，重点关注问题的可解性（solvability）和难度（difficulty）。ScaleQuest使用经过QFT训练后的模型生成问题集合，并通过GPT-4o-mini对问题的可解性和难度进行进一步优化。优化后的问题作为正样本，源问题作为负样本，构建偏好对进行DPO优化。
3. 问题筛选 生成的问题至此仍存在一些小问题，因此采用了筛选方法进行处理，包括语言筛选、可解性筛选和难度采样。 语言筛选: 问题生成模型仍然会生成大量其他语言的数学问题，约占 20%。由于我们的重点是英文数学问题，因此我们通过识别包含非英文字符的问题并筛除这些样本，来去除非英文问题。 可解性筛选: 尽管 QPO 有效地提升了生成问题的可解性，但仍有一些问题不合逻辑。主要原因包括：(1) 问题约束不完善，出现缺失条件、冗余条件或逻辑不一致的情况，(2) 问题没有产生有意义的结果（例如，涉及人数的问题应得到非负整数作为答案）。为筛除此类样本，我们使用 Qwen2-Math-7B-Instruct 评估问题是否有意义以及条件是否充分。 难度采样: 基于DeepSeekMath-7B训练了一个难度打分器模型，然后去除生成数据中难度很低的一些样本。
4. 回答生成与奖励筛选 使用Qwen2-Math-7B-Instruct生成回答，并将奖励模型的评分作为评估回答质量的指标。从5个候选回答中选择奖励评分最高的回答，作为最终的回答。