现实世界中诸多问题需进行序列决策,其中每个决策的结果具有概率性与不确定性,且后续行动的可选性受先前行动结果制约。生成适应不确定性、全局最优且随状态空间扩展仍可扩展的策略至关重要。本文提出生成最优决策树(规定不同结果场景下的应执行动作,同时最大化策略期望收益),结合动态规划与混合整数线性优化方法,利用问题特定信息剪除状态空间中无收益贡献的子集,使方案适用于大规模有限状态空间问题。实验证明所提方法能以线性时间复杂度(相对于探索状态数量)找到全局最优决策树。
序列决策是兵棋推演、医疗与网络作战等领域的核心问题。在此类场景中,智能体采取行动达成目标,但每项行动的产出具有离散性、概率性与不确定性,导致面对多可能未来时难以确定最优行动。此外,可用行动存在复杂条件依赖性(制约策略可能性),同时需考虑远期收益。本文开发了一种方法,用于定义适应不同行动结果的最优决策序列,并以决策树形式呈现。
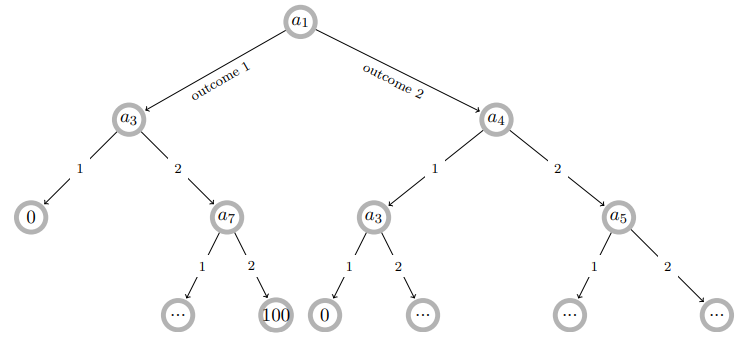
尽管决策树是机器学习中成熟模型,但其传统用途为预测——预测型决策树(DT)的每个分叉对应已知数据特征的组合(其对应结果未知)。而在行动方案(CoA)生成场景中,决策树的应用转向策略生成,允许基于先前行动的不确定结果定义最优行动序列。如图1所示:CoA树的每个节点代表系统状态并规定一项行动,其执行结果引发状态变迁(通过行动结果的概率性分支转移至子节点,可触发新行动)。树终止于叶节点(行动预算耗尽、状态不允许新行动或目标达成获取收益)。
图1:含二元分叉的最优决策树示例(各节点为带行动指令的状态)
本研究核心贡献为生成全局最优决策树的算法与优化模型。这些决策树在最大化策略期望收益的同时,兼顾行动与结果间的复杂依赖关系。通过动态规划(DP)与混合整数优化(MIO)结合,利用问题特定信息剪除状态空间无效子集,使方法可扩展至大规模状态空间问题。虽非首个提出通过部分行动剪枝缩减状态空间的研究(如Pinto与Fern 2014年工作),但本方法在最终决策模型中不牺牲全局最优性。通过示例验证方法有效性,并在随机生成测试案例中展示计算效率——尤其值得注意的是,本方法能以线性时间复杂度(相对于探索状态数)找到最优决策树。
所提框架可生成符合以下特征问题的全局最优决策树:
- 智能体采取具离散概率结果的行动(改变环境状态)
- 状态捕获环境所有相关信息及智能体历史行动信息
- 决策空间有限,终止于目标达成或无可用行动
- 行动可具复杂依赖关系,例如:
• 先决条件:须先执行某行动并达成特定结果方可尝试后续行动
• 排除条件:若执行某行动并达成特定结果则禁止尝试其他行动
如第3节示例所示,行动间依赖关系可通过行动与结果的逻辑关系集进行数学与图形化表达。