【NeurIPS2023】因果成分分析

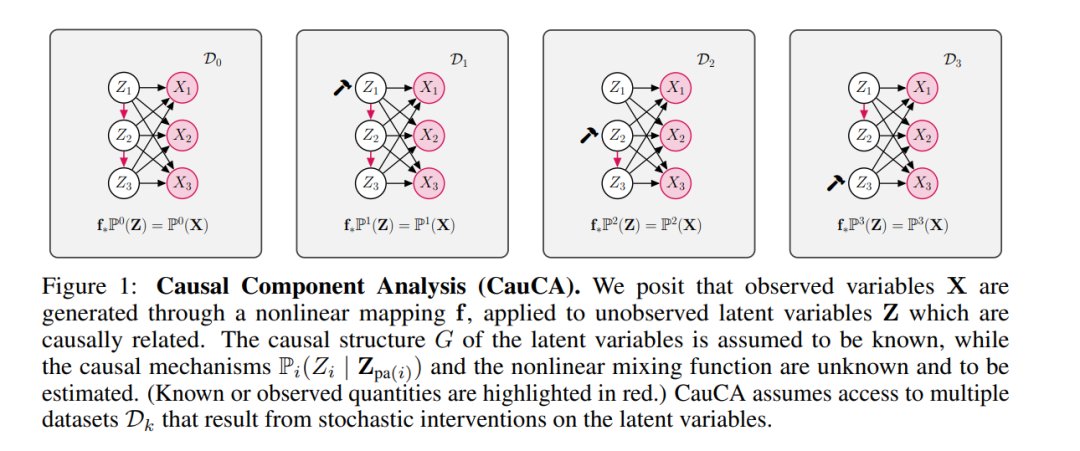
独立成分分析（ICA）旨在从观测混合物中恢复独立的潜在变量。因果表示学习（CRL）则旨在推断因果相关（因此通常统计上依赖的）潜在变量，以及编码其因果关系的未知图。我们引入了一个中间问题，称为因果成分分析（CauCA）。CauCA可以被视为ICA的泛化，模拟潜在成分之间的因果依赖性，并作为CRL的一个特殊情况。与CRL相比，它预设了因果图的知识，专注于学习解混函数和因果机制。在CauCA中恢复基本真理的任何不可能性结果也适用于CRL，而可能性结果可能作为扩展到CRL的垫脚石。我们从通过对潜在因果变量进行不同类型干预生成的多个数据集中，表征了CauCA的可识别性。作为一个推论，这种干预视角还为非线性ICA带来了新的可识别性结果——CauCA的一个特殊案例，具有一个空图——相比以往的结果需要明显更少的数据集。我们引入了一种基于似然的方法，使用规范流来估计解混函数和因果机制，并通过在CauCA和ICA设置中的广泛合成实验来证明其有效性。