【纽约大学博士论文】对称神经网络理论，148页pdf

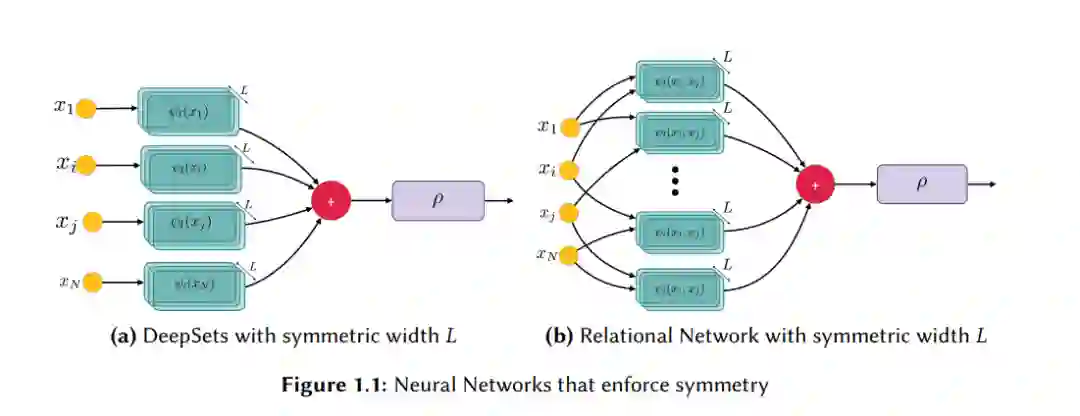
这篇论文探讨了对称神经网络的理论，这是一种在设计、实现和分析保持对称性质的神经网络时使用的概念和数学框架。在这里，对称性可能涉及到神经网络架构或其组件在某些变换下保持不变的性质。例如，这可能包括旋转或平移不变性。 对称函数，它们以一个无序的、固定大小的集合作为输入，在基于不可区分点或粒子的多种物理场景中找到了实际应用，并且也被用作构建具有其他不变性网络的中间构建块。已知通过强制执行排列不变性的神经网络可以普遍表示对称函数。然而，表征典型网络的近似、优化和泛化的理论工具未能充分表征强制执行不变性的架构。 这篇论文探讨了何时可以将这些工具适应于对称架构，以及何时不变性质本身导致了全新的理论发现。我们研究并证明了对称神经网络扩展到无限大小输入时的近似限制、对称和反对称网络相对于集合元素之间的互动的近似能力，以及通过梯度方法学习简单对称函数的可学习性。 深度学习理论始于通用逼近定理，乐观地说，人们可能希望这就是理论的全部。在无限数据的极限情况下，似乎没有必要超越两层的标准神经网络。但无论数据集变得多大，实践者仍然寻求应用某种先验知识来改善优化和泛化。 通常，这种先验知识是根据数据的性质来适配的。例如，自注意力机制似乎是处理序列数据的适当先验[Vaswani et al. 2017]。但往往，这种先验知识采取的是底层对称性的形式。 经典地，图像数据从强制执行平移等变性的架构中获得巨大益处[LeCun et al. 1998]。同样，对于图数据，我们执行对节点重新标记的不变性[Scarselli et al. 2008]；对于分子，我们执行旋转不变性[Cohen et al. 2018]；对于费米子波函数，我们执行反对称性[Moreno et al. 2021]等等。 对于集合，适当的几何先验是排列不变性[Zaheer et al. 2017; Qi et al. 2017; Santoro et al. 2017]。集合数据在粒子物理或人口统计的设置中自然出现。但排列不变性也是其他架构内部应用的基本原语，特别是对于图[Kipf and Welling 2016]和反对称波函数[Pfau et al. 2020]。因此，我们将排列不变性架构视为自成一体的首要公民，值得显式研究。 这段讨论强调了在深度学习架构中应用先验知识的重要性，特别是当这些先验与数据的内在对称性相关时。通过理解和应用这些对称性原则，可以设计出更有效的深度学习模型，这些模型不仅能够更好地理解数据的几何和结构特性，而且能够更有效地进行优化和泛化，即使在数据量巨大的情况下也是如此。