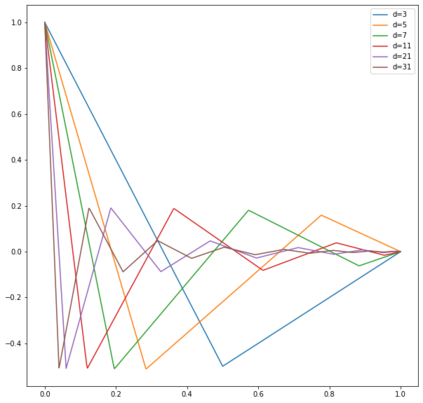
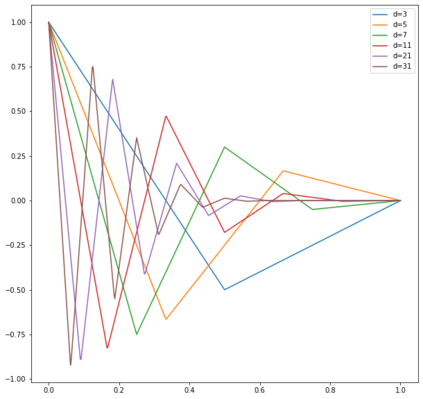
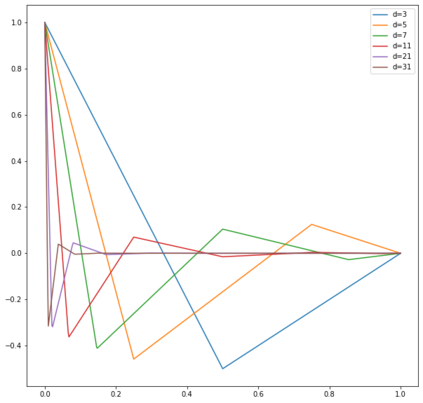
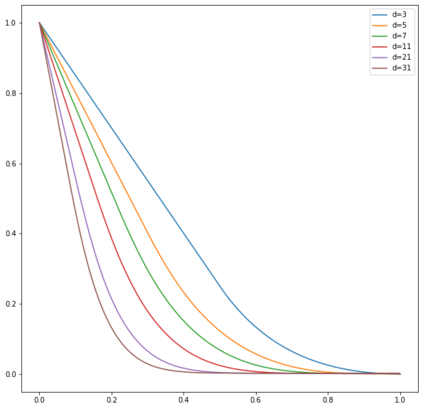
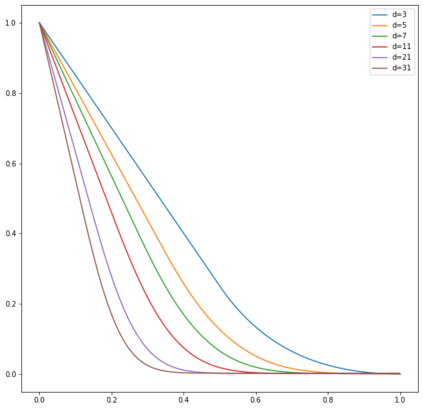
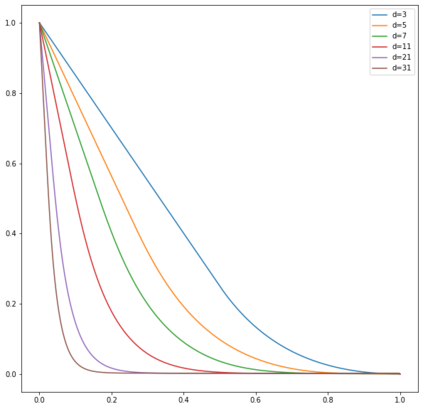
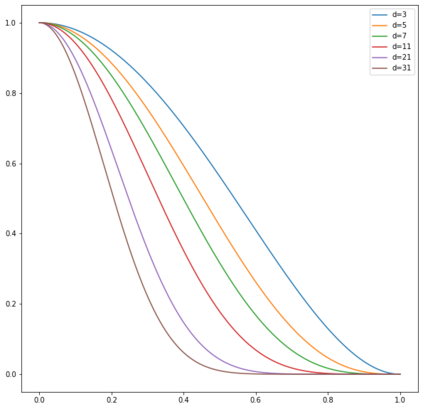
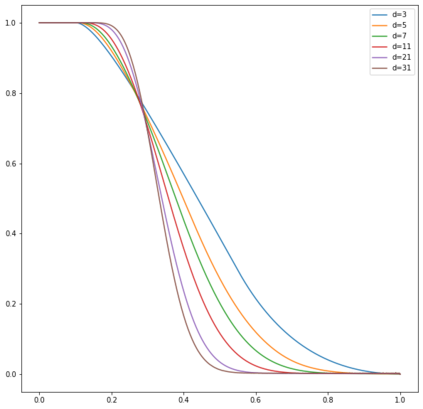
In this note, we study how neural networks with a single hidden layer and ReLU activation interpolate data drawn from a radially symmetric distribution with target labels 1 at the origin and 0 outside the unit ball, if no labels are known inside the unit ball. With weight decay regularization and in the infinite neuron, infinite data limit, we prove that a unique radially symmetric minimizer exists, whose weight decay regularizer and Lipschitz constant grow as $d$ and $\sqrt{d}$ respectively. We furthermore show that the weight decay regularizer grows exponentially in $d$ if the label $1$ is imposed on a ball of radius $\varepsilon$ rather than just at the origin. By comparison, a neural networks with two hidden layers can approximate the target function without encountering the curse of dimensionality.
翻译:在本说明中,我们研究了单隐层神经网络和RELU激活的内插数据如何从一个目标标签1的对称分布中得出,目标标签1在源头和单元球外0,如果单球内没有已知的标签。随着重量衰变和无限神经,无限数据限制,我们证明存在一个独特的对称最小化器,其重量衰变常数分别增长为美元和美元。我们进一步表明,如果将1美元标注加在半径$\varepsilon的球上,而不是仅仅在源头,则重量衰减定器会以美元指数增长。相比之下,两个隐藏层的神经网络可以在不遭遇天性诅咒的情况下接近目标功能。