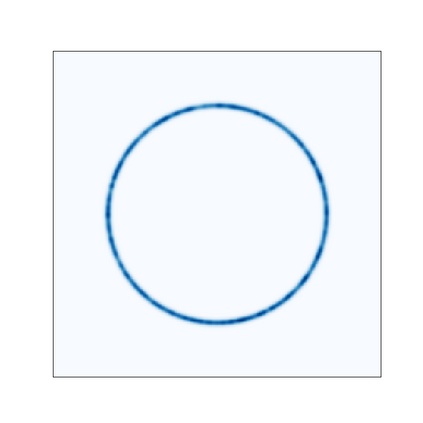
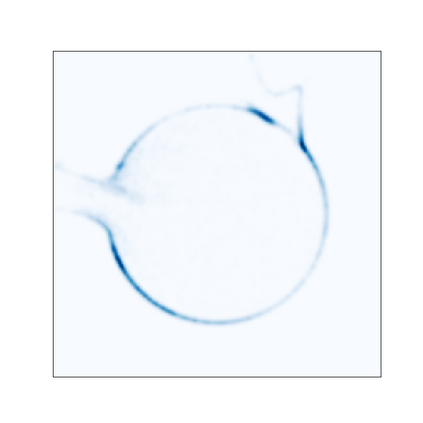
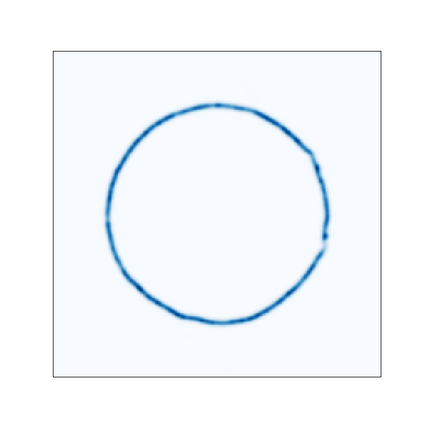
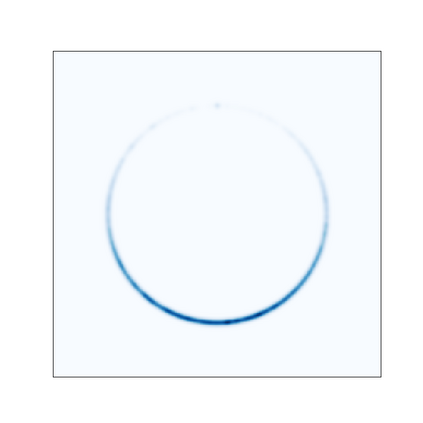
Normalizing Flows (NFs) are flexible explicit generative models that have been shown to accurately model complex real-world data distributions. However, their invertibility constraint imposes limitations on data distributions that reside on lower dimensional manifolds embedded in higher dimensional space. Practically, this shortcoming is often bypassed by adding noise to the data which impacts the quality of the generated samples. In contrast to prior work, we approach this problem by generating samples from the original data distribution given full knowledge about the perturbed distribution and the noise model. To this end, we establish that NFs trained on perturbed data implicitly represent the manifold in regions of maximum likelihood. Then, we propose an optimization objective that recovers the most likely point on the manifold given a sample from the perturbed distribution. Finally, we focus on 3D point clouds for which we utilize the explicit nature of NFs, i.e. surface normals extracted from the gradient of the log-likelihood and the log-likelihood itself, to apply Poisson surface reconstruction to refine generated point sets.
翻译:普通化流程(NFs)是灵活的、明显的基因模型,已经展示了这些模型,以准确模拟复杂的真实世界数据分布。然而,它们的不可视性制约限制了位于高维空间内低维元体的数据分布。实际上,这一缺陷往往被绕过,在影响所产生样品质量的数据中添加噪音。与先前的工作不同,我们通过从原始数据分布中生成样本来解决这一问题,同时充分了解周遭分布和噪声模型。为此,我们确定,在受过环数据培训的NFs隐含地代表了最大可能性区域的多元。然后,我们提出了一个优化目标,即从透度分布样本中回收该元体上最可能的点。最后,我们侧重于3D点云,为此我们使用了NFs的明确性质,即从原木状分布的梯度和对日志相似性本身提取的表层正常值。我们用Poisson表面重建来改进生成的点集。