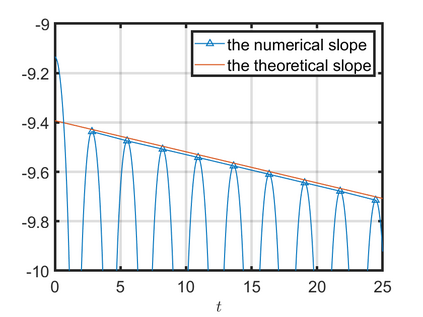
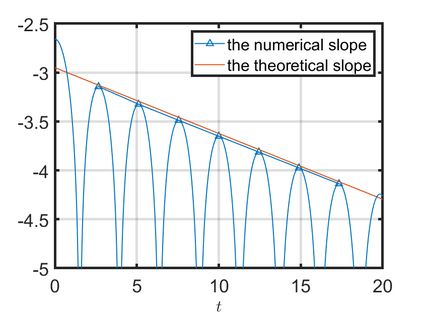
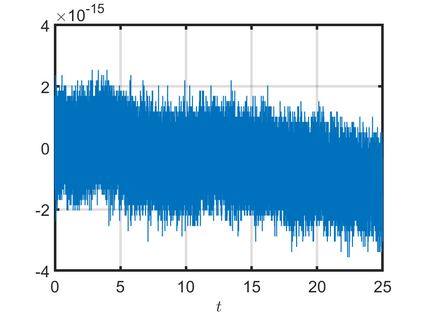
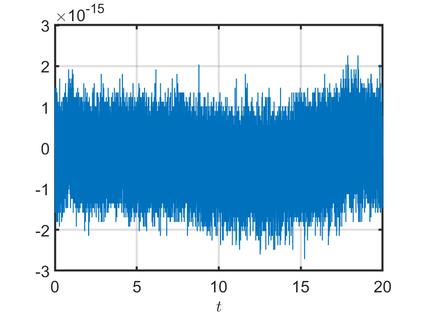
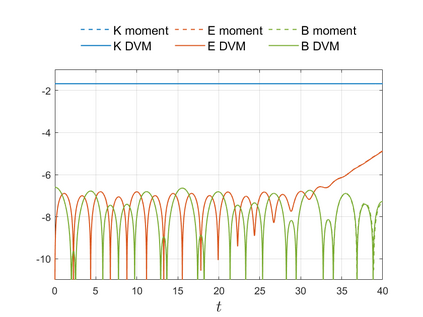
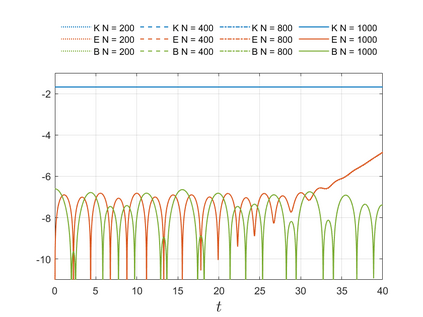
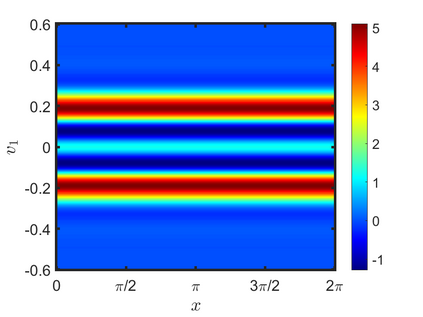
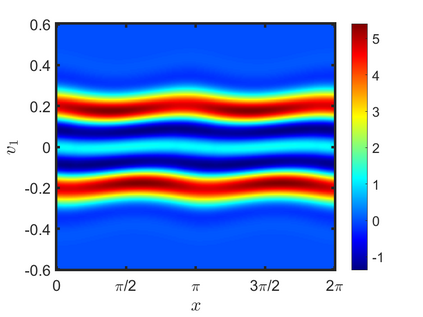
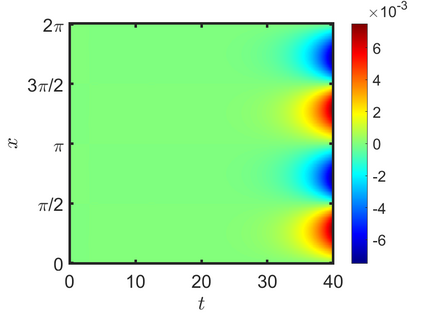
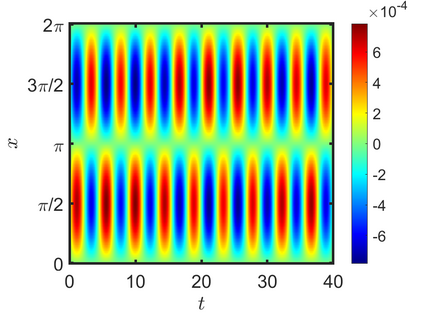
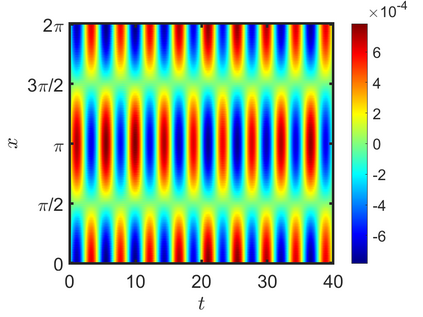
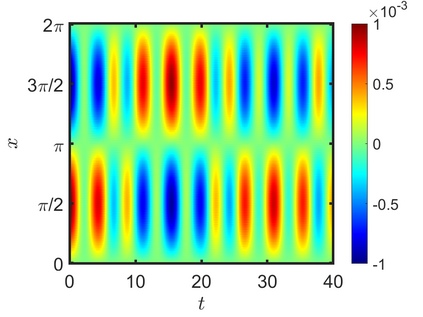
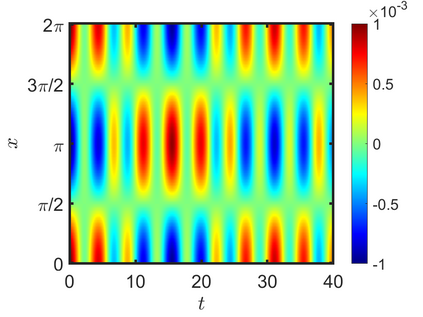
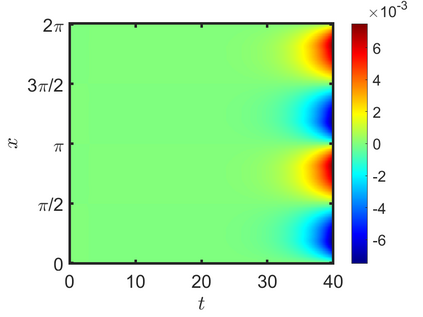
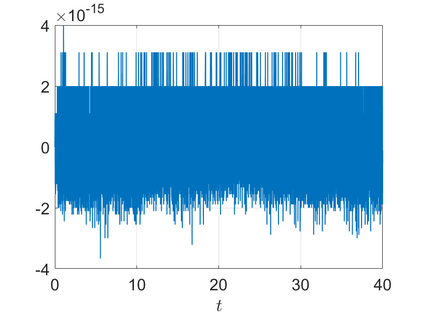
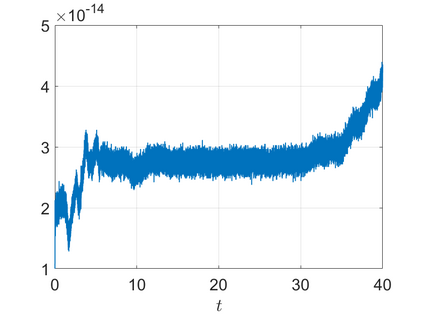
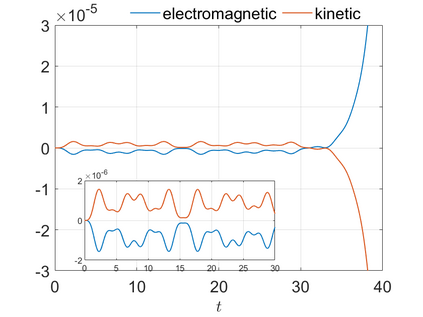
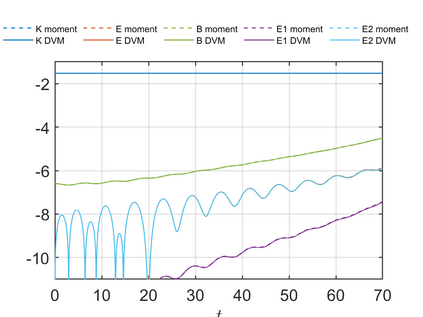
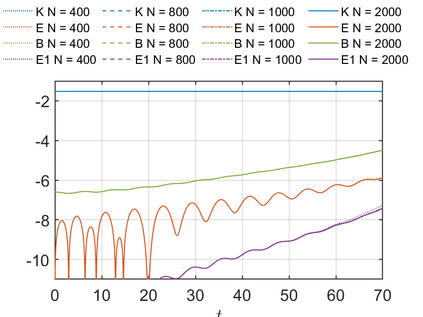
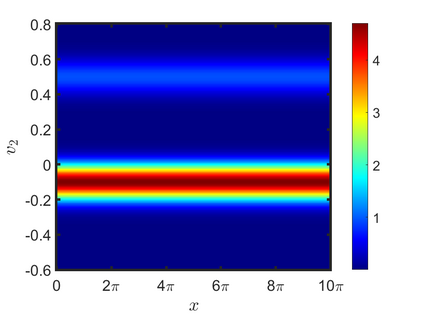
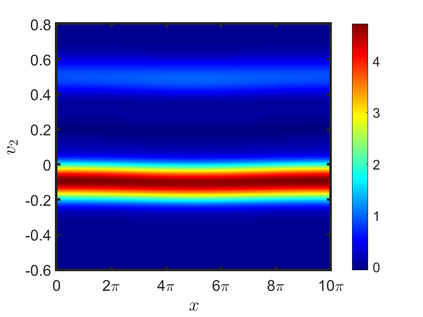
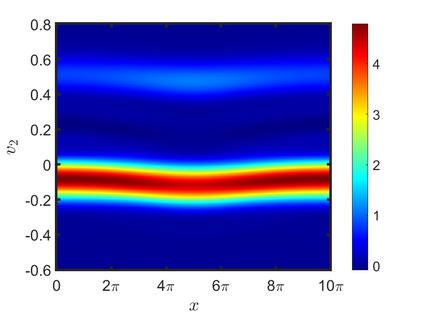
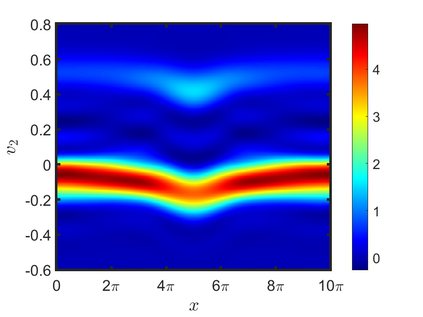
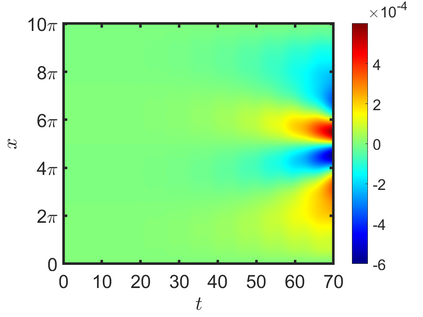
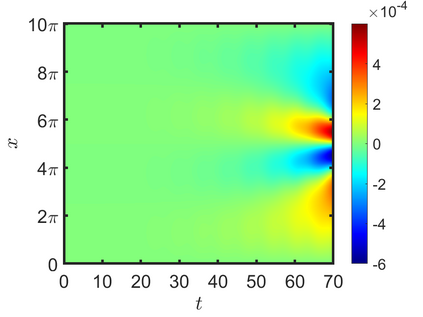
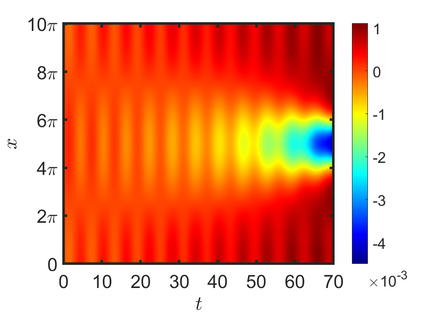
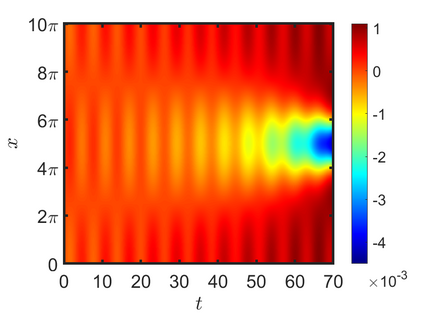
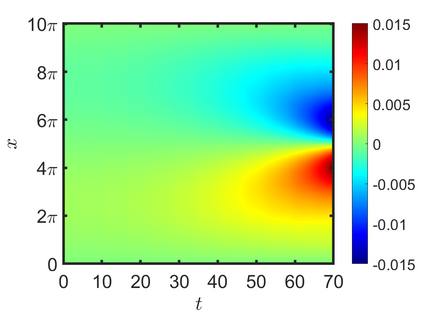
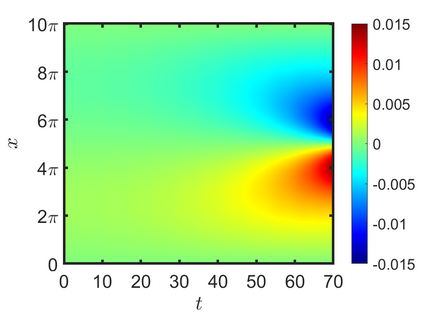
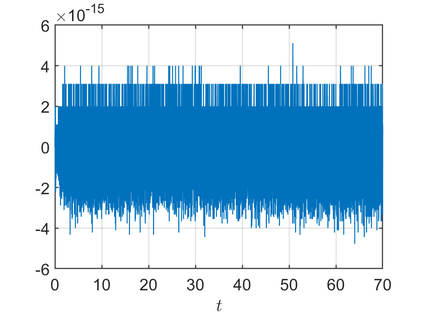
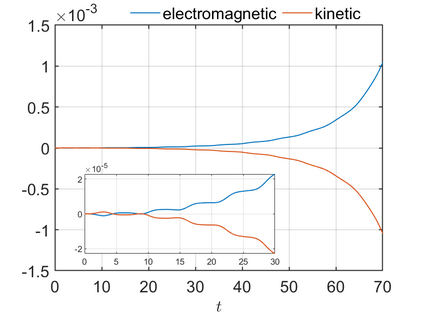
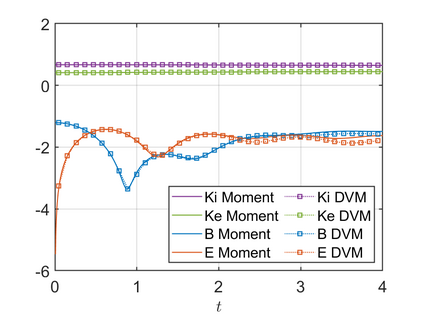
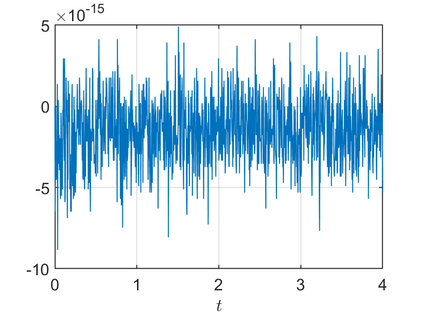
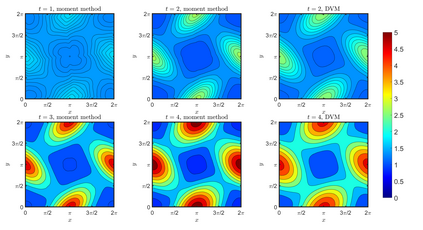
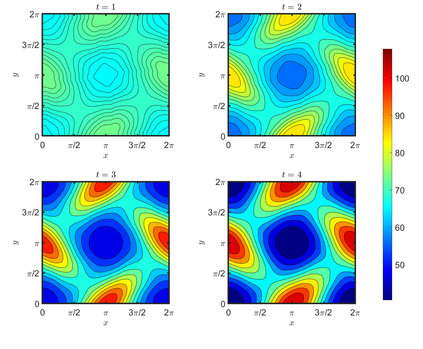
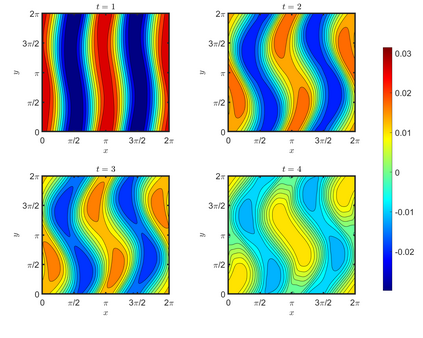
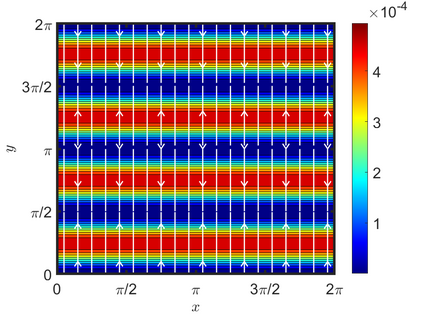
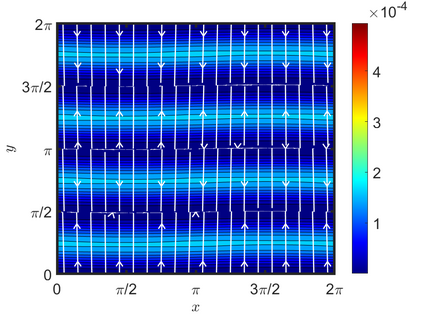
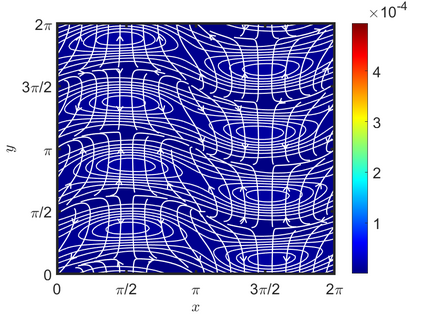
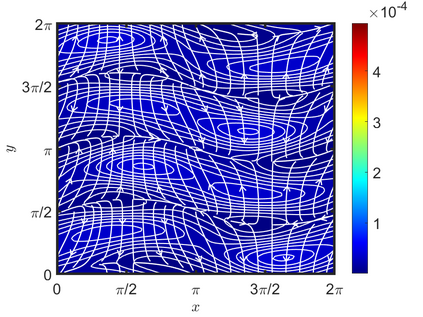
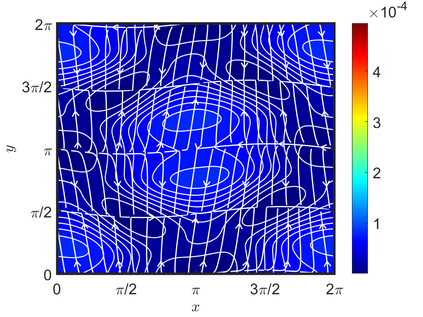
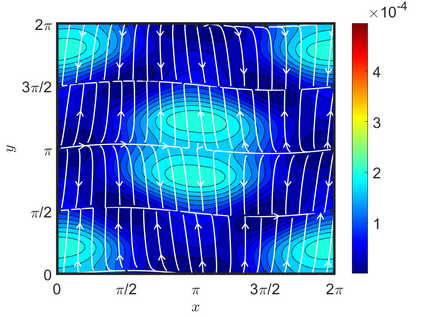
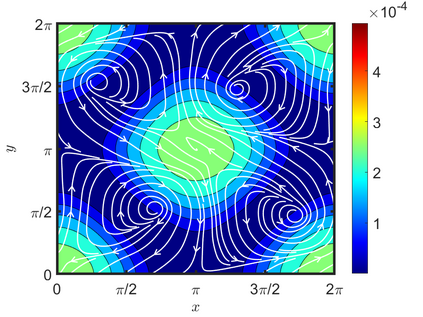
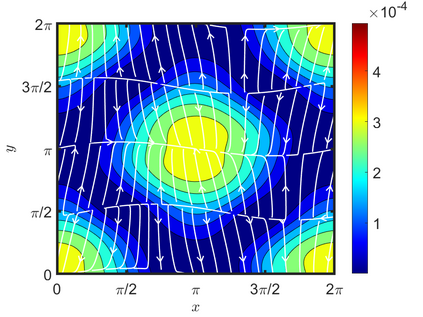
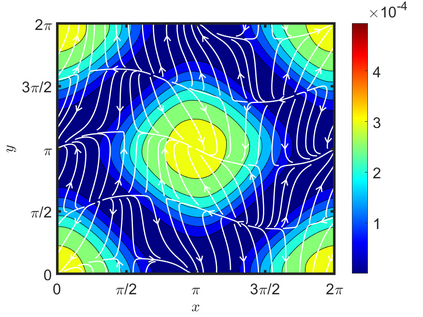
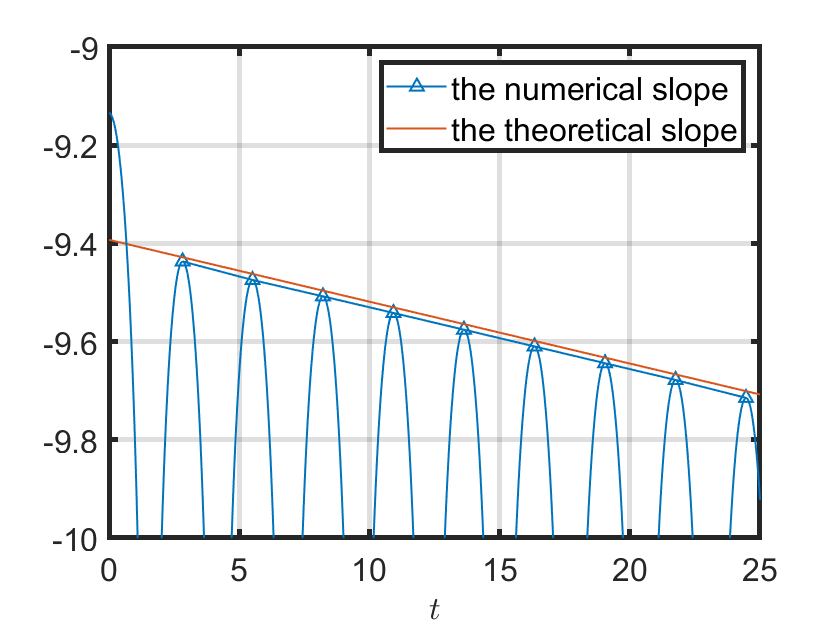
We present an energy-conserving numerical scheme to solve the Vlasov-Maxwell (VM) system based on the regularized moment method proposed in [Z. Cai, Y. Fan, and R. Li. CPAM, 2014]. The globally hyperbolic moment system is deduced for the multi-dimensional VM system under the framework of the Hermite expansions, where the expansion center and the scaling factor are set as the macroscopic velocity and local temperature, respectively. Thus, the effect of the Lorentz force term could be reduced into several ODEs about the macroscopic velocity and the moment coefficients of higher order, which could significantly reduce the computational cost of the whole system. An energy-conserving numerical scheme is proposed to solve the moment equations and the Maxwell equations, where only a linear equation system needs to be solved. Several numerical examples such as the two-stream instability, Weibel instability, and the two-dimensional Orszag Tang vortex problem are studied to validate the efficiency and excellent energy-preserving property of the numerical scheme.
翻译:我们提出了一个基于[Z. Cai, Y. Fan, 和 R. Li. CPAM, 2014] 中提议的定时法解决Vlasov-Maxwell(VM)系统的节能数字方案。在Hermite扩展框架下,为多维VM系统推导出全球超曲时间系统,在此框架下,扩张中心和缩放因子分别被设定为宏观速度和当地温度。因此,Lorentz 任期的影响可以降低为若干关于宏观速度和较高时间系数的数值,这可以大大降低整个系统的计算成本。提出了一种节能数字方案,以解决瞬间方程和马克斯韦尔方程,只需要解决一个线性方程系统。正在研究若干数字实例,如二流不稳定、韦贝尔不稳定和二维的Tang Tang vortex 问题,以确认数字方案的效率和良好的节能特性。